Quick Sort

Chào các bạn!
Tiếp theo chuỗi series về các thuật toán sắp xếp và tìm kiếm căn bản, thì ở bài viết này mình sẽ trình bày các bạn phần thuật toán Sắp xếp nhanh - Quick Sort.
Được mệnh danh là một trong các thuật toán sắp xếp nhanh, hiệu quả và dễ implement nhất! Chúng ta cùng tìm hiểu xem nó sao nhé!

Đặt vấn đề

Cho một dãy số kích thước N phần tử, hãy sắp xếp dãy số đó theo thứ tự tăng dần.

Ở bài viết trước, mình đã trình bày về giải thuật Selection Sort, thì ta đã thấy rằng, nhược điểm duy nhất của nó là... quá chậm.
Và trong một số ứng dụng, điều này là không thể chấp nhận.
Vậy nên từ đó, người ta đã nghĩ ra một giải pháp chạy nhanh hơn, thay thế cho Selection Sort với độ phức tạp thuật toán nhỏ hơn $O(n*logn)$ (tuy nhiên, không phải lúc nào cũng đúng bằng $n*logn$ nhé mn).

Ý tưởng thuật toán

Thuật toán chia làm 3 bước sau đây:

1. Nếu dãy số đã cho có không quá 1 phần tử, thì coi như dãy số đã được sắp xếp. Không cần làm gì thêm.

2. Trong trường hợp dãy số nhiều hơn 1 phần tử thì, chia dãy số đã cho ra làm 2 nửa:

   • Nửa bên trái bao gồm các số $\lt X$
   • Nửa bên phải bao gồm các số $\geq X$

   với $X$ là một giá trị nào đó (thuộc dãy số đã cho).

3. Tiếp tục, lặp lại bước 1, bước 2 ở trên với 2 dãy con vừa chia đôi một cách độc lập.

Dưới đây là hình minh họa cho thuật toán này (nguồn ảnh)

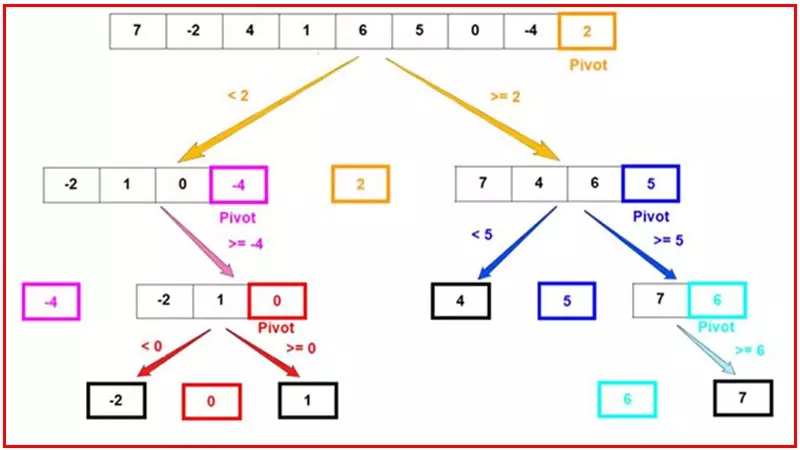
Có 2 điểm quan trọng nhất của thuật toán này mà bạn cần nắm chắc. Chỉ cần chắc nó, thì coi như bạn đã hiểu rõ thuật toán QuickSort, để rồi không cần phải học thuộc hay copy code gì nữa... 2 điểm đó là:

1. Ý tưởng chính của thuật toán là: chia để trị (chia bài toán lớn thành các bài toán tương tự, nhưng nhỏ hơn)
2. Nhưng chia như thế nào? Cách chọn giá trị $X$ là điểm mấu chốt!

Dưới đây là đoạn code mẫu mình đã chuẩn bị:

void quickSort(int *arr, int l, int r) { if (l >= r) return; int i = l, j = r; int X = arr[random(l, r)]; while (i < j) { while (arr[i] < X) i++; while (arr[j] > X) j--; if (i <= j) swap(arr[i++], arr[j--]); } quickSort(arr, i, r); quickSort(arr, l, j);
} 

Xem full code chương trình: https://ideone.com/RsQXHA