Tìm Hiểu Công Thức Toán Của Phương Pháp Hồi Quy Tuyến Tính Qua Bài Toán Dự Báo Xả Lũ (Understanding The Linear Regression)

Xin chào, hôm nay chúng ta cùng học ít toán nhé ! Cám ơn bạn đã quan tâm đến bài viết của Tôi

TỔNG QUAN VẤN ĐỀ

Mô Tả Bài Toán

Khi nước lũ chảy về khiến mực nước trong hồ thủy điện dâng lên và cần phải xả lũ để giữ an toàn cho đập thủy điện. Như vậy cần phải tính toán việc xả nước lượng nước là bao nhiêu để đảm bảo án toàn. Nhóm em sẽ thực nghiệm hệ thống dự báo xả lũ để giải quyết vấn đề trên. Vấn đề dự báo xả lũ có rất nhiều giải pháp thuật toán di truyền (GA), tối ưu hóa đàn kiến (ACO) và phương pháp tối ưu hóa bầy đàn (PSO),… . Trong đó có phương pháp hồi quy tuyến tính (linear regression). Hệ thống sẽ thu thập dữ liệu có sẵn về lưu lượng xả lũ và mực nước trong hồ để đưa ra hàm dự báo $f(x)=ax+b$ để qua đó dự báo lượng nước xả lũ khi có số liệu về mực nước trong hồ.

Giải Pháp Liên Quan

Vấn đề dự báo xả lũ có rất nhiều giải pháp như thuật toán di truyền (GA), tối ưu hóa đàn kiến (ACO), phương pháp tối ưu hóa bầy đàn (PSO), phương pháp tối ưu bầy mèo (CSO), … . Đặc điểm chung của các mô hình này là việc tìm kiếm bộ $w= [α,β]$ trong không gian theo cách ngẫu nhiên và cập nhập sau mỗi lần tính toán để có thể tiệm cận với nghiệm tối ưu. Tập nghiệm của các giải pháp này có thể tốt hoặc không tốt phù thuộc vào các lần tạo ngẫu nhiên điểm bắt đầu. Nói một cách đơn giản đó là ta giải bài toán tối ưu lõm (hoặc lồi). Phương pháp hồi quy tuyến tính dưới đây tôi sẽ chứng minh lại công thức toán của phương pháp để có thể giải chính xác được bài toán dự báo với dữ liệu tuyến tính và rời rạc.

Bạn có thể xem thêm bài viết của tôi về tối ưu hóa bầy mèo (cat swarm optimization)

Mô tả phương pháp hồi quy tuyến tính

Mô tả phương pháp tối ưu bầy mèo

PHƯƠNG PHÁP HỒI QUY TUYẾN TÍNH

Hiểu Công Thức Toán

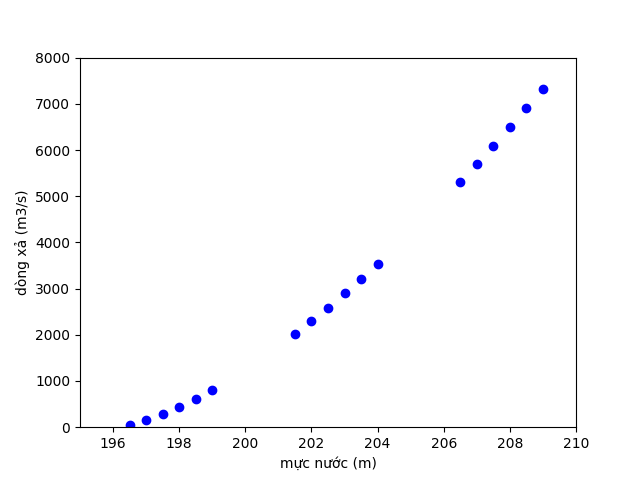
Cho tập dữ liệu các điểm trên mặt phẳng $O_{xy}$ và $D = {(x_i,y_i)}| i ∈[0,N]$. Tìm hàm dự báo sao cho thỏa mãn phương trình đó có dạng $y=ax+b$ được mô ta như sau:

Hình 1: Mô tả các điểm dữ liệu.

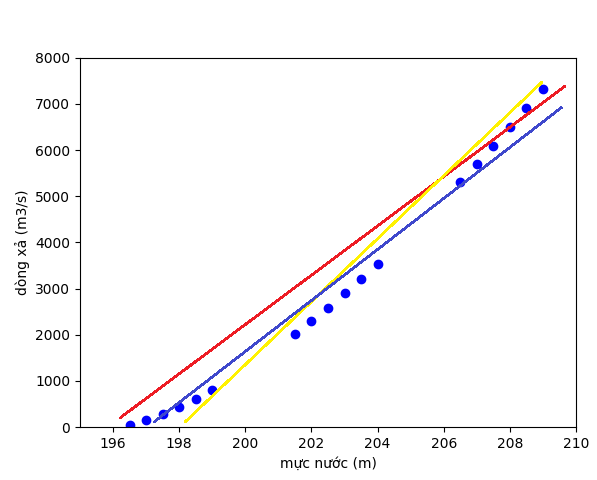
Hình 2: Mô tả các đường thẳng.

Trong hình 2 ta thấy có nhiều đường thẳng tiệm cận với các điểm dữ liệu. Và phương pháp hồi quy tuyến tính sẽ giúp tìm ra hàm dự báo tối ưu nhất với tập dữ liệu đang xét. Ta mô tả bài toán trên dưới dạng phương trình như sau:

$\begin{bmatrix} y_0 = a x_0 + b\\ y_1 = ax_1+ b\\ ....\\ y_n = ax_0 + b\\ \end{bmatrix} (1) \iff \begin{bmatrix} y_0 \\ y_1 \\ ....\\ y_n \\ \end{bmatrix} = a \times \begin{bmatrix} x_0\\ x_1\\ ....\\ x_n\\ \end{bmatrix} + b \times \begin{bmatrix} 1\\ 1\\ ....\\ 1\\ \end{bmatrix} (2)$

Ta gọi $y^T=[y_0,y_1,… ,y_n], x^T= [x_0,x_1,…,x_n], c^T= [1,1,…,1] , a_1=ax^T , a_2=b c^T$. Ta biểu diễn mô phỏng hình vẽ với dữ liệu giả định trong không gian 3 chiều như sau:

Hình 3: Không gian 3 chiều.

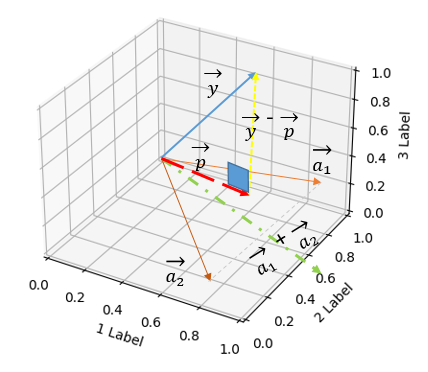
Ta thấy $\overrightarrow{y}$ không thuộc mặt phẳng $H_{12}$ được tạo bởi 2 vector $\overrightarrow{a_1}$ và $\overrightarrow{a_2}$ vì các điểm dữ liệu không thẳng hàng và cũng không cùng nằm trên một mặt phẳng. Do đó ta cần tìm $\overrightarrow{y'}$ ~ $\overrightarrow{y}$ và thuộc $H_{12}$. Thật may đó là ta luôn biết rằng hình chiếu của $\overrightarrow{y}$ lên $H_{12}$ sẽ gần tương đồng với chính nó và nằm trên $H_{12}$ ta gọi đó $\overrightarrow{p}$ . Vậy vấn đề hiện tại đó là tìm $\overrightarrow{p}$, ta biểu diễn $\overrightarrow{p}$ như sau:

$p= α ×x^T+ β × c^T (3)↔p= \begin{bmatrix} a\\ b\\ \end{bmatrix} × [x^T c^T] (4)$

Ta đặt $v_1= x^T , v_2= c^T, w= \begin{bmatrix} a\\ b\\ \end{bmatrix}$ $\Leftrightarrow p= w ×V$ . Mặt khác ta lại thấy ($\overrightarrow{y}$ - $\overrightarrow{p}$) vuông góc với 2 vector $\overrightarrow{v_1}$ và $\overrightarrow{v_2}$ nên tích vô hướng của chúng sẽ bằng 0. Ta biểu diễn như sau:

$\begin{cases} v_1 \times (\overrightarrow{y} - \overrightarrow{p}) = 0 \\ v_2 \times (\overrightarrow{y} - \overrightarrow{p}) = 0 \end{cases} \Leftrightarrow \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix} \times (\overrightarrow{y} - \overrightarrow{p}) = 0$

Ta đặt $V^T= \begin{bmatrix} v_1\\ v_2\\ \end{bmatrix}$, ta có phương trình:

$V^T×(y-p)=0 (7)$

$\Leftrightarrow V^T×y-V^T×p=0 (8)$

$\Leftrightarrow V^T×y-V^T× w×V =0 (9)$

$\Leftrightarrow w= (V^T× V)^{(-1)} × V^T×y (10)$

Vậy ta đã tính được $w= \begin{bmatrix} a\\ b\\ \end{bmatrix}$ theo phương trình 10.

Áp Dụng Bài Toán

Như đã mô tả bài toán ở trên ta cùng xem xét bảng dữ liệu:

Bảng 1: Dữ liệu đầu vào

Dựa vào bảng dữ liệu này, ta sẽ cố gắng dự đoán lượng xả nước nhờ mực nước trong hồ chứ. Đầu tiên cầu khái báo thư viện xử dụng:

python 2 and python 3
import numpy as np
import matplotlib.pyplot as plt

Sau đó ta khai báo dữ liệu và biểu diễn trên một biểu đồ 2D:

if __name__ == '__main__': dong_xa_oy = np.array([[55, 156, 287, 442, 618, 812, 2016, 2297, 2590, 2894, 3210, 3536, 5317, 5701, 6094, 6496, 6906, 7325]]).T muc_nuoc_ox = np.array([[196.5, 197., 197.5, 198., 198.5, 199., 201.5, 202., 202.5, 203., 203.5, 204., 206.5, 207., 207.5, 208., 208.5, 209.0]]).T oxy_array = [195, 210, 0, 8000] plt.xlabel('mực nước (m)') plt.ylabel('dòng xả (m3/s)') plt.plot(muc_nuoc_ox, dong_xa_oy, 'bo') plt.show() 

Hình 4: Phân bổ dữ liệu

Hàm tính nghiệm theo phương trình 10:

def linear_regression(y_vector, v_matrix): w_1 = np.linalg.pinv(np.dot(v_matrix.T, v_matrix)) w_2 = np.dot(v_matrix.T, y_vector) w = np.dot(w_1, w_2) return w

Xử lý dữ liệu để tính toán:

b_vector = np.array(np.ones((muc_nuoc_ox.__len__(), 1)))
a_matrix = np.concatenate((b_vector, muc_nuoc_ox), axis=1)
liner_vector = linear_regression(dong_xa_oy, a_matrix)

Kết quả tính toán w:

Solution found by me: w = [[-116539.37979331 590.34411187]]

Bây giờ, ta sẽ dùng thử thư viện sklearn.linear_model để so sánh kết quả:

from sklearn import linear_model
lin_model = linear_model.LinearRegression(fit_intercept=False)
lin_model.fit(a_matrix, dong_xa_oy)
print('Solution found by sk-learn: w = ', lin_model.coef_)
print('Solution found by me: w = ', liner_vector.T)

So sánh kết quả :

Solution found by sk-learn: w = [[-116539.37977378 590.34411178]]
Solution found by me: w = [[-116539.37979331 590.34411187]]

Hình 5: Kết quả của Quang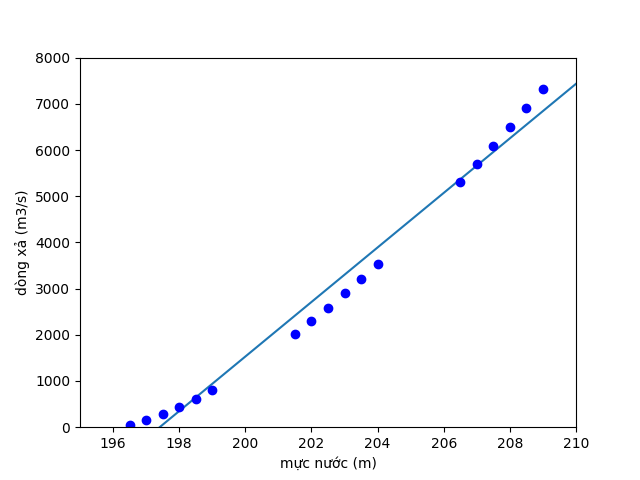

Hình 6: Kết quả của sklearn model

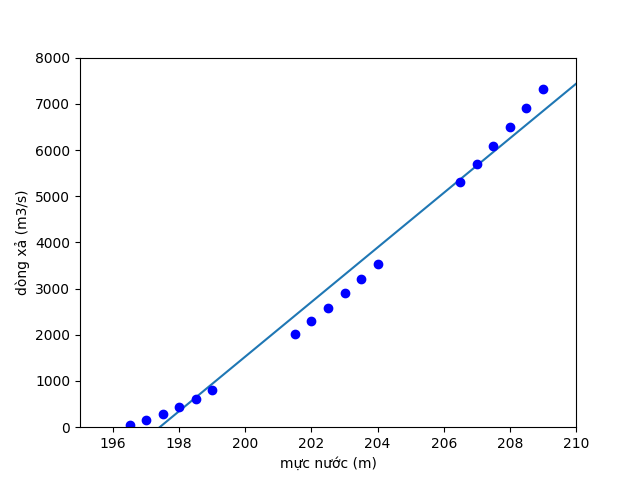
Ta thử dự đoán với mực nước là 200m, 205m thì cần xả khối lượng nước là bao nhiêu:

b = liner_vector[0][0]
a = liner_vector[1][0]
x_linear = np.array([200, 205])
y_linear = x_linear * a + b
print('Mực nước lần lượt là', x_linear[0], 'và', x_linear[1])
print('Lượng xả dự báo lần lượt là:', round(y_linear[0], 2), 'và', round(y_linear[1], 2))

Kết quả:

Mực nước lần lượt là 200 và 205
Lượng xả dự báo lần lượt là: 1529.44 và 4481.16

Ghi chú: Tải toàn bộ mã nguồn tại github

Hạn chế của phương pháp

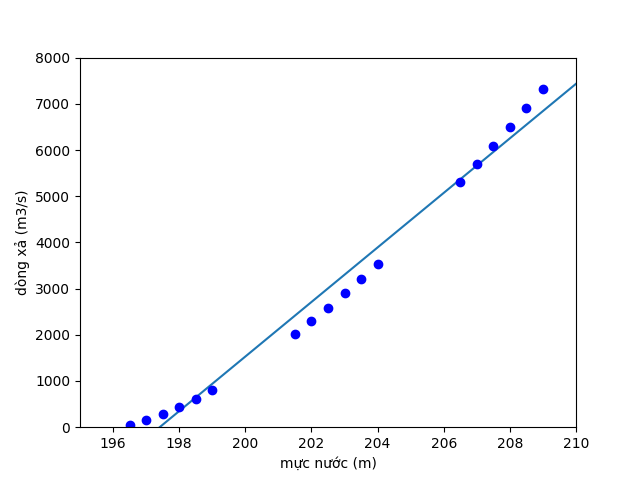
Hạn chế đầu tiền là với tập dữ liệu đẹp thì ta có thể dễ dàng dự báo chính xác được lượng xả lũ. Nhưng trong trường hợp dữ liệu bị nhiễu do sai lệch trong quá trình thu thập thì sẽ rất khó khăn trong quá trình dự báo. Hãy cùng xem hình sau:

Hình 7: Dữ liệu bị nhiễu gây sai lệch

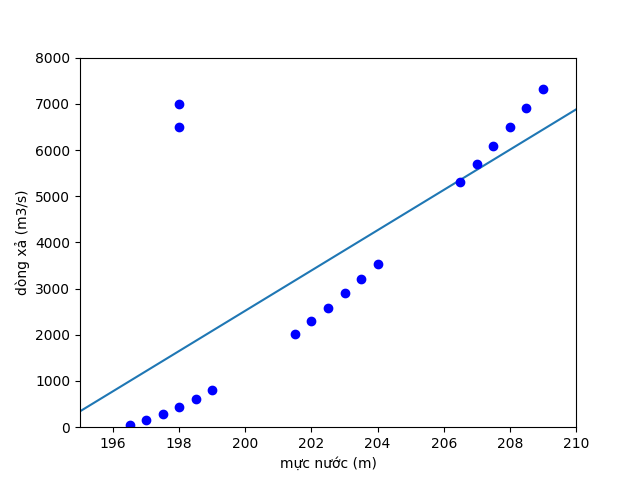
Do đó khi xây dựng hàm dự báo trước tiên chúng ta cần xử lý dữ liệu nhiễu để tránh gây sai lệch trong quá trình tính toán ( Bước này được gọi là tiền xử lý ). Hạn chế thứ hai đó là hồi quy tuyến tính không thể biểu diễn được các mô hình phức tạp mặc dùng dữ liệu đầu vào cho ta thấy dữ liệu không nhất thiết phải tuyến tính nhưng các mối quan hệ đó vẫn khá đơn giản so mới nhiều mô hình trong khác trong thực tế như parabol, sin,… .

Nhận xét

Hồi quy tuyến tính là một mô hình đơn giản, lời giải cho phương trình đạo hàm bằng 0 cũng khá đơn giản. Tuy nhiên trong một số các trường hợp dữ liệu ra thu thập được là tuyến tính ta vẫn có thể sử dụng mô hình để dự báo. Phương pháp có ưu điểm tốt hơn các giải thuật tối ưu bầy đàn.

Tài Liệu Tham Khảo

[1]. wikipedia, linear regression.

[2]. Ths. Lê Xuân Cầu. Xây dựng biểu đồ vận hành khẩn cấp kiểm soát lũ. Viện khoa học khí tượng thủy văn và biến đổi khí hậu. Tạp chí khí tượng thủy 01/2015 p22-p26.