Mở bài

Do lười viết Viblo nên mình đã đi chơi CTF bù, và sau đó bài này hay quá nên mình lại lọc cọc lên gõ mấy dòng để chia sẻ với mọi người Sau khi dành ra hơn 16 tiếng liên tục nghĩ chall này thì mình đã giải được, và kết thúc cuộc thi ở vị trí thứ 71, thua nónlá một câu và hơn KCSC 1 tí :'> Scoreboard có thể được tham khảo tại đây.

Ngoài ra, câu này đáp án gốc của tác giả sử dụng một Turing machine rồi dịch ngược về ruleset, nên sẽ phức tạp hơn lời giải của mình nhiều

Ý tưởng chính

Về cơ bản, đề bài yêu cầu đưa ra một danh sách các string replacement patterns để có thể convert được từ chuỗi đầu vào thành đầu ra yêu cầu. Đây là bài toán thuộc class Markov algorithm, mà cả tác giả lẫn mình đều chưa biết trước khi làm bài này =))

Phần chính của đề bài có 2 function như sau:

def read_substitution(string): substitution = tuple(s.strip() for s in string.split('=>')) return substitution if len(substitution) == 2 else ('', '')

Hàm này sẽ đọc replacement rule string 'find => replacement' mà chúng ta đưa vào, và trả về tuple (find, replace). Tuple này là các rules chúng ta sẽ chạy lần lượt qua input string: tìm tất cả các substring find và thay thế chúng bằng replace.

def test_substitution(substitutions, string): def substitute(s, a, b): initial = s s = s.replace(a, b) return (s, not s == initial) # s ^ 2 rounds for string of length s for _ in range(len(string) ** 2): performed_substitute = False for find, replace in substitutions: string, performed_substitute = substitute(string, find, replace) # once a substitute is performed, go to next round if performed_substitute: break # if no substitute was performed this round, we are done if not performed_substitute: break return string

Đơn giản là chúng ta sẽ chạy tối đa $s^2$ rounds, trong đó mỗi round chúng ta sẽ sử dụng replacement rule đầu tiên thành công (string có thay đổi sau replacement). Nếu tất cả các rule set của chúng ta không làm thay đổi đầu vào thì chúng ta sẽ dừng sớm cho nhanh.

Mình sẽ bỏ qua phần giới hạn $s^2$ rounds, vì chúng ta có thể cải thiện tốc độ thuật toán bằng cách thêm các replacement rules nữa

^{The algorithm improvement is trivial and is left as an exercise to the readers.}

Đề bài và lời giải

Level 1

def level_1(): initial = f'{"0" * randint(0, 20)}initial{"0" * randint(0, 20)}' target = initial.replace('initial', 'target') return (initial, target)

Đầu vào là một chuỗi gồm các số 0, từ initial, và các số 0 khác, và đầu ra là chỉ thay thế từ initial thành từ target. Đề bài đã bao gồm lời giải luôn rồi (orz)

rules_1 = [ 'initial => target',
]

Level 2

def level_2(): initial = ''.join( rand.choice(['hello', 'ginkoid']) for _ in range(randint(10, 20)) ) target = initial.replace('hello', 'goodbye').replace('ginkoid', 'ginky') return (initial, target)

Tương tự thì đề bài đã bao gồm lời giải rồi Lúc mình làm bài này thì mình còn không đọc đề bài nên đưa ra một lời giải khác, nhưng kết quả không thay đổi.

rules_2 = [ 'hello => goodbye', 'oid => y'
]

ginkoid là tên một admin của kỳ thi này.

Level 3

def level_3(): return ('a' * randint(10, 100), 'a')

Đầu vào là một chuỗi các chữ cái a, và đầu ra là 1 chữ cái a. Ý tưởng thì chúng ta đầu tiên sẽ nghĩ đến việc xóa chữ a, nhưng nếu chỉ làm thế thì chuỗi cuối cùng sẽ là chuỗi rỗng. Vậy, chúng ta phải thiết kế rule mà sau khi xóa vẫn phải không rỗng:

rules_3 = [ 'aa => a',
]

Level 4

def level_4(): return ('g' * randint(10, 100), 'ginkoid')

Gần giống với Level 3, đầu vào là chuỗi các chữ g, và đầu ra là ginkoid. Ý tưởng đầu tiên là sử dụng đúng thuật toán trên và cuối cùng thay thế g thành ginkoid, nhưng nếu như thế thì thuật toán sẽ không dừng, do trong chuỗi ginkoid có chữ g, và ruleset đó sẽ cho chúng ta kết quả không dừng là ginkoidinkoidinkoid...

Vậy bây giờ phải làm gì? Mình chọn là sửa solution level 3 sao cho đầu ra là gg thay vì g, và xử lý được vấn đề trên vì ginkoid không có 2 chữ g liên tiếp.

rules_4 = [ 'ggg => gg', 'gg => ginkoid',
]

Level 5

def level_5(): random_string = ''.join( str(randint(0, 1)) for _ in range(randint(25, 50)) ) initial = random_string initial += rand.choice(['', '0', '1']) initial += random_string[::-1] if rand.randint(0, 1): return (f'^{initial}$', 'palindrome') else: shuffled = list(initial) rand.shuffle(shuffled) return ( f'^{"".join(shuffled)}$', 'not_palindrome' )

Bỏ qua đề bài cho nhanh, vì thực ra có xác suất đề bài sai =)) Tác giả plz-

Cơ mà, đầu vào là chuỗi binary string có delimiter ^01101010$, và đầu ra là palindrome nếu đây là chuỗi đối xứng, và not_palindrome nếu ngược lại. Mình khuyên mọi người nghĩ bài này trước khi đọc lời giải, vì nó vui lắm =)) Mình nghĩ mất 14 tiếng liên tục (không tính thời gian ăn uống). Bài này có khá nhiều vấn đề, trong đó chính có 2 cái chính:

• Chúng ta không được dùng regex, nên chúng ta không so sánh 2 đầu được.
• Chúng ta muốn xử lý các chữ cái từ 2 đầu lại đều nhau, nhưng do ruleset theo thứ tự, nên có thể nó sẽ chỉ xử lý từ 1 đầu trở lại và mặc kệ đầu kia.

Xử lý 2 vấn đề trên sẽ ra được lời giải của mình, ý tưởng chính là như sau:

• Dịch dần con trỏ vào chính giữa input string, rồi sau đó so sánh 2 bên.
• Sử dụng một kỹ thuật mà mình tạm gọi là stopper, đó là chèn một ký tự lạ vào 2 đầu string lúc cần để replacement rule không tìm được đầu chuỗi mà thay thế.

Để dịch con trỏ vào giữa thì khá đơn giản đúng không:

rules_5_bad = [ '^0 => 0^', '^1 => 1^', '0$ => $0', '1$ => $1',
]

Tuy nhiên vấn đề 2 xảy ra ngay lập tức: giả sử chúng ta có chuỗi ^0000$, thì thay vì ra được chuỗi mong muốn 00^$00, do rule '^0 => 0^' nằm trên cùng nên luôn được thực hiện trước, và cho chúng ta kết quả không như mong muốn là 0000^$. Vậy chúng ta muốn là rules của chúng ta phải xử lý 1 chữ cái đầu và 1 chữ cái cuối, rồi sau đó mới tiếp tục chạy: mình thêm chữ cái stopper lạ vào ngay cạnh delimiter để ruleset của mình không tìm ra đầu string, và khi xử lý xong đủ 2 đầu thì mình mới gỡ stopper đi:

rules_5_good = [ # read the first char and stops '^0 => 0^*', '^1 => 1^*', # read the last char and stops '0$ => *$0', '1$ => *$1', # after reading both, remove the stopper to continue reading '* => ',
]

Với ruleset này, chuỗi đầu vào ^0000$ sau 2 step đầu tiên sẽ ra 0^*00*$0, và sau khi gỡ stopper * đi thì chúng ta lại tiếp tục đọc vào 2 chữ cái 2 đầu nữa. Cuối cùng, chúng ta sẽ đến được center của chuỗi đầu vào, và giờ là đến lúc xử lý tính đối xứng:

rules_5_symmetry = [ # if the string length is odd, remove the center character '^0$ => ^$', '^1$ => ^$', # if the string is symmetric, keep processing '0^$0 => ^$', '1^$1 => ^$', # otherwise, fail it rightaway '0^$1 => X', '1^$0 => X', # else, we hit the good ending '^$ => palindrome',
]

Có vài điểm quan trọng cần để ý:

• 2 rules đầu tiên của phần này cần phải được ưu tiên hơn phần đọc chuỗi vào trung tâm, vì nếu không ^0$ sẽ bị dịch thành 0^$, và cho dù là chắc nếu như vậy thì vẫn có thể sửa solution cho ra đáp án đúng, tuy nhiên nó sẽ khác với thiết kế lời giải của mình, và debug sẽ rất khó.
• Nếu tất cả các rules đã pass mà không có thay đổi gì, điều đó ám chỉ rằng tất cả yêu cầu về đối xứng đã thỏa mãn, và chuỗi chỉ còn lại ^$: từ đó chúng ta replace anchors với chuỗi cuối cùng là palindrome
• Nếu chuỗi của chúng ta có bất cứ điểm nào không đối xứng, trong chuỗi sẽ bị xóa anchor ^$, và thay vào đó sẽ là ký tự X cho biết là chuỗi không đối xứng: chúng ta phải thiết kế một cái sink hút hết chữ cái trong chuỗi và trả về liền là not_palindrome:

rules_5_sink = [ 'X0 => X', 'X1 => X', '0X => X', '1X => X', 'X => not_palindrome',
]

Rules trên sẽ hút toàn bộ các chữ cái 0 và 1 và bỏ qua chúng. Tương tự với phần trên, sau khi pass hết phần hút chữ cái thì còn lại mỗi chữ X, và chúng ta trả về kết quả cuối cùng là not_palindrome. Ngoài ra, do khi gặp X thì thuật toán chúng ta phải short-circuit hủy, nên cái sink này phải đặt trên cùng ưu tiên hơn tất cả phần còn lại. Ghép lại 3 phần, chúng ta ra được đáp án cuối cùng:

rules_5 = [ # failure sink 'X0 => X', 'X1 => X', '0X => X', '1X => X', 'X => not_palindrome', # if the string length is odd, remove the center character '^0$ => ^$', '^1$ => ^$', # if the string is symmetric, keep processing '0^$0 => ^$', '1^$1 => ^$', # otherwise, fail it rightaway '0^$1 => X', '1^$0 => X', # else, we hit the good ending '^$ => palindrome', # read the first char and stops '^0 => 0^*', '^1 => 1^*', # read the last char and stops '0$ => *$0', '1$ => *$1', # after reading both, remove the stopper to continue reading '* => ',
]

Tổng cộng mất 17 rules, trong khi đề bài cho giới hạn tận 100 rules lận

Level 6

def level_6(): first_number = randint(0, 255) second_number = randint(0, 255) answer = first_number + second_number result = 'correct' # random chance that answer is wrong if rand.randint(0, 1): answer = randint(0, 511) if not answer == first_number + second_number: result = 'incorrect' # convert all to string representations numbers = [ bin(first_number)[2:], bin(second_number)[2:], bin(answer)[2:] ] # chance to pad a number or answer if randint(0, 1): index = randint(0, 2) numbers[index] = '0' * randint(1, 3) + numbers[index] # chance to make padded number additionally wrong if randint(0, 1): result = 'incorrect' numbers[index] = '1' + numbers[index] return (f'^{numbers[0]}+{numbers[1]}={numbers[2]}$', result)

Tương tự với level 5, mình xin quote lại câu mình vừa viết ở trên:

Bỏ qua đề bài cho nhanh, vì thực ra có xác suất đề bài sai =)) Tác giả plz-

Về cơ bản thì đề bài sẽ cho chúng ta một phép cộng nhị phân kiểu như ^01010+000111=1101011$, và chúng ta phải thay thế thành correct nếu phép toán đó đúng, hoặc incorrect nếu ngược lại.

Chúng ta mở đầu bằng lời giải Turing machine của tác giả mà mình không hiểu gì =))

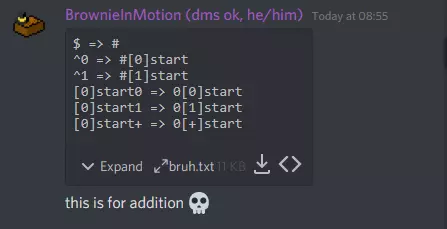
Bài này thì mình chỉ nghĩ mất có gần 2 tiếng thôi Sau một thời gian suy nghĩ làm thế nào để lưu carry trong chuỗi, bỗng một ý tưởng nảy lên trong đầu: chúng ta sử dụng ruleset để chuyển từ dạng nhị phân thành dạng unary (đơn phân? nhất phân?), rồi sau đó dùng pattern matching để dần dần trừ 1 cả 2 vế. Đây chính là phần Markov algorithm mà mình sử dụng.

Phần chuyển từ binary sang unary khá đơn giản nhưng lại vô cùng thú vị:

rules_6_baseconv = [ '|0 => 0||', '1 => 0|', '0 => ',
]

Trong đó có 3 rules đơn giản:

• Nếu có các giá trị unary trước số 0, thì chúng ta phải shift left, tương đương với nhân 2. Điều đó đồng nghĩa với việc là chúng ta dịch số 0 sang bên trái và nhân đôi số vạch
• Nếu có bit 1, thì điều đó tương đương với bit 0 (nhân 2 giá trị unary ở trước) và 1 vạch (+1). Phương pháp này tương tự với Horner's method mình có đề cập trong bài về các phép nhân nhanh.
• Cuối cùng, sau khi các shifting ở trên được thực hiện xong, thì chúng ta xóa hết các số 0 lẻ.

Sau đó chúng ta bắt đầu match dần các vạch bên phép cộng và kết quả:

rules_6_cancelling = [ # cancel 2nd summand '|=| => =', # cancel 1st summand '|+=| => +=',
]

Rule đầu trong bộ trên sẽ xóa 1 vạch ở cả số hạng thứ 2 và tổng, và rule 1 sẽ xóa ở số hạng thứ nhất và tổng với điều kiện rằng số hạng thứ 2 đã xóa hết về 0. Nếu thành công, chúng ta sẽ có được tổng rỗng, và trả về correct:

rules_6_success = [ '^+=$ => correct',
]

Nếu số hạng thứ 2 (hoặc số hạng 1, hoặc tổng) chưa được xóa hết trong khi vế còn lại đã hết rồi, chúng tả sử dụng kỹ thuật failure sink ở trên và đánh dấu fail:

rules_6_failure = [ '|=$ => X', '|+=$ => X', '^+=| => X'
]

Trong đó, rule đầu tiên là khi tổng về 0 nhưng số hạng thứ 2 vẫn còn lớn hơn 0, rule thứ 2 là khi tổng và số hạng thứ 2 về 0 nhưng số hạng thứ nhất vẫn lớn hơn 0, và rule thứ 3 là khi cả 2 số hạng đều là 0 nhưng tổng vẫn lớn hơn 0. Sau đó chúng ta thêm cái sink hút X ở trên đầu như level 5:

rules_6_sink = [ '^X => X', 'X$ => X', 'X+ => X', '+X => X', '|X => X', 'X| => X', 'X => incorrect',

Ghép lại tất cả và chúng ta ra được đáp án hoàn chỉnh:

rules_6 = [ # failure sink '^X => X', 'X$ => X', 'X+ => X', '+X => X', '|X => X', 'X| => X', 'X => incorrect', # binary to unary '|0 => 0||', '1 => 0|', '0 => ', # cancelling out the sum '|=| => =', '|+=| => +=', # good ending '^+=$ => correct', # bad endings '|=$ => X', '|+=$ => X', '^+=| => X'
]

Như đã đề cập ở trên:

Mình sẽ bỏ qua phần giới hạn $s^2$ rounds, vì chúng ta có thể cải thiện tốc độ thuật toán bằng cách thêm các replacement rules nữa

Do phương pháp này chuyển từ binary về unary, nên độ phức tạp nhảy lên $O(2^n)$, vượt quá giới hạn của đề bài là $O(n^2)$. Để giải quyết vấn đề này, chúng ta có thể thêm vào các rules sao cho cancel nhanh hơn: đề bài cho giới hạn tận 300 rules, trong khi chúng ta mới sử dụng có 16. Tuy nhiên, phần này khá đơn giản, và nếu bạn hiểu phần mình vừa viết ở trên thì sẽ rất dễ nhận ra cách cải tiến - nên mình để lại làm bài tập về nhà cho độc giả

The algorithm improvement is trivial and is left as an exercise to the readers.

Kết bài

Level 6 là một ví dụ cho việc sử dụng Markov algorithm. Đây là một bài toán khá hay nhưng mình chưa tìm hiểu kỹ nên chưa viết một bài Viblo về nó được

Cảm ơn các bạn đã đọc bài này, và hẹn các bạn vào lần sau!