Bài viết được lấy từ https://truongphuoc.wordpress.com/2024/09/30/blockchain-20-6-block-cipher-mode-of-operation/

Xin chào các bạn, sau một thời gian nghỉ viết do vấn đề cá nhân, mình lại trở lại rồi đây. Để hoàn thiện các bài viết liên quan tới mật mã học, hôm nay chúng ta sẽ cùng tìm hiểu về Block cipher mode of operation và Galois/Counter Mode nhé.

Mở bài

Cùng nhắc lại một chút về mã hóa đối xứng nào, trong bài hệ mật đối xứng, mình đã trình bày về cách hoạt động của thuật toán AES. Thuật toán AES là một thuật toán mã hóa khối, có nghĩa là dữ liệu plaintext được chia ra thành các khối để đưa vào mã hóa từng khối, với độ dài cố định là 128bit.

Một câu hỏi ra là nếu như độ dài dữ liệu plaintext nhiều hơn rất nhiều so với 128bit thì sao? Tất nhiên là chúng ta sẽ chia plaintext thành các phần 128bit rồi. Nhưng có một vấn đề là bản thân các thuật toán mã hóa khối như AES chỉ làm việc hiệu quả với từng khối (block) thôi, chúng ta phải có cách thức, thuật toán nào đó để có thể làm việc với nhiều khối khác nhau. Do đó ta có Block cipher mode of operation.

Block cipher mode of operation

Block cipher mode of operation diễn tả cách thức lặp đi lặp của một thuật toán mã hóa khối để có thể mã hóa một chuỗi các khối hiệu quả và bảo mật. Mình cùng tìm hiểu một vài mode nhé

Sáu block cipher mode phổ biến để mã hóa dữ liệu (Nguồn: Wikipedia)

Electronic codebook (ECB)

Đây là thuật toán đơn giản nhất, ta sẽ mã hóa từng khối riêng lẻ, sau đó nối chúng lại với nhau.

Ưu điểm của mode này là nhanh, chúng ta có thể mã hóa song song (Encryption parallelizable), giải mã song song (Decryption parallelizable) và có thể truy cập bất cứ block nào tùy ý (Random read access).

Nhược điểm của ECB là nó thiếu tính khếch tán, tức là khi plaintext giống nhau thì nó sẽ ra kết quả giống nhau.

Cipher block chaining (CBC)

Trong CBC mode, mỗi block plaintext trước khi mã hóa sẽ cộng (phép XOR nhé) với kết quả của block cipher trước đó rồi mới mã hóa. Điều này làm cho các cipher block phía sau dựa vào cipher block phía trước. Để có thể tạo ra sự ngẫu nhiên cho kết quả, trong lần mã hóa block đầu tiên người ta cộng (nhắc lại là phép XOR nha) với một giá trị ngẫu nhiên, gọi là initialization vector (IV). IV này là một giá trị ngẫu nhiên có độ dài bằng với độ dài của block plaintext (để dễ cộng đó mà). Cùng xem hình minh họa sau

CBC được dùng rất phổ biến trong mã hóa, nó có một hạn chế là phải mã hóa tuần tự và phải padding block cuối cùng (xem padding ở bài mã hóa đối xứng).

Counter (CTR)

Trong counter mode, chúng ta sẽ mã hóa (nonce || count) trước, sau đó sẽ cộng (XOR) với plaintext để ra ciphertext. Chú ý phép || là phép nối nha, xem hình là hiểu liền.

Nói một chút về nonce, nonce chính là một initialization vector (IV) như CBC nhưng chỉ được sử dụng một lần duy nhất (thế nên mới gọi là nonce 🤣). Còn counter là một số tăng liên tiếp. Ví dụ trong AES thì đầu vào là 128bit, ta thích một counter = 32bit thì thì IV sẽ là 128-32=96bit.

CTR vừa có ưu điểm nhanh, có thể Encryption parallelizable, Decryption parallelizable và Random read access. Đồng thời nó cũng khếch tán dữ liệu, mỗi lần encrypt khác nhau là sử dụng một IV khác nhau mà.

MAC

Người ta nhận thấy rằng các mode trên chỉ cung cấp tính bí mật (confidentiality) cho dữ liệu, mà không cho biết dữ liệu có bị sửa đổi, hay thay thế hay không (Nếu có người sửa một vài bit của ciphertext thì có trời mới biết 🤣) . Thế nên phải có một cơ chế nào đó để cung cấp tính xác thực (authenticity) cho dữ liệu.

Để xác thực, khi gửi ciphertext chúng ta có thể gửi kèm một mã nào đó, mã này có nhiệm vụ xác thực người gửi là chính chủ và kiểm tra tính toàn vẹn của ciphertext. Người ta gọi mã này là Message authentication code hay MAC.

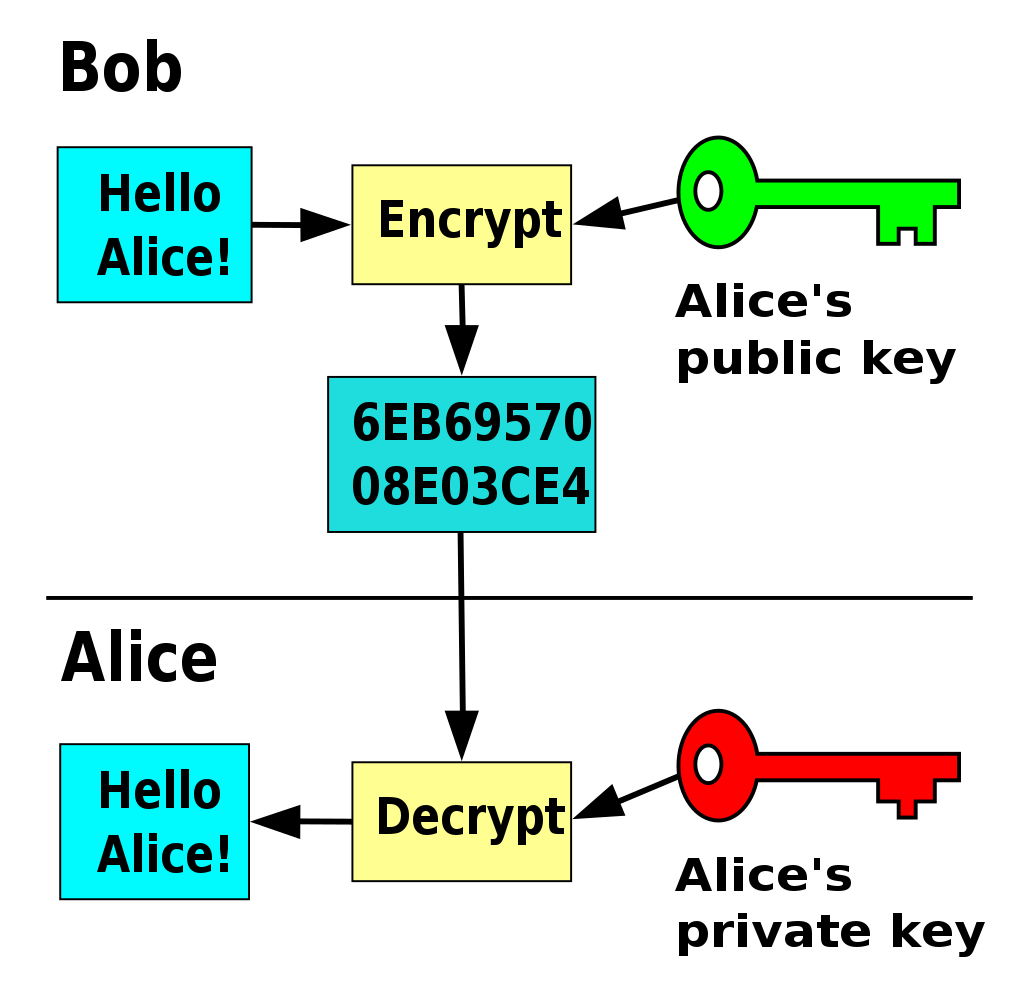
Một cách để làm được điều này là ký điện từ (signature digital). Người gửi có thể ký vào ciphertext và gửi chữ ký kèm với ciphertext, người nhận sẽ sử dụng public key của người gửi để xác thực.

Ngoài ra người ta có kết hợp giữa chế độ bảo mật (confidentiality mode) và chế độ xác thực (authenticity mode) để tạo thành một thuật toán cung cấp cả sự bảo mật và xác thực, gọi là authenticated encryption hay AE. Chúng ta sẽ cùng tìm hiểu một thuật toán đó bên dưới.

GCM

Phần này chúng ta sẽ cùng tìm hiểu về GCM cho thuật toán mã hóa đối xứng với đầu vào là 128 bit. Ví dụ điển hình là thuật toán AES.

Encryption

Galois/Counter Mode là một AE mode, nó là sự kết hợp giữa Counter mode (CTR) và phép nhân trong Galois Field (GF). Sơ đồ mã hóa của nó như sau:

Chúng ta thấy được sự kết hợp ở đây.

Phần trong khung màu đỏ mình có kẻ ở trên là counter mode, rất dễ thấy phải không nào, đầu ra của nó là một chuỗi các ciphertext. Phần này cung cấp tính bảo mật cho plaintext như đã nói ở trên.

Phần còn lại cung cấp tính xác thực, với "ngôi sao" của chúng ta là phép nhân trong trường Galois.

Mình sẽ đi chi tiết từng phép toán, thành phần nhé.

Counter

Các giá trị Counter0, Counter1, Counter2 ở trên là sự kết hợp giữa IV và Counter như trình bày ở phần CTR. Trong đó IV có độ dài 96bit và Counter có độ dài 32bit (để tạo thành chuỗi 128 ấy mà).

Có một sự khác biệt ở đây so với Counter Mode: GCM sử dụng counter0 cho quá trình xác thực, nên quá trình Encryption bắt đầu từ Counter1.

Ek

Ek là thuật toán mã hóa khối với key là k. Ví dụ ta có thể sử dụng thuật toán AES.

Phép ⊕

Tất cả các phép ⊕ ở trên hình là phép XOR. Nếu ai không nhớ phép XOR là gì thì học lại nha 🤣👌

Auth data 1

Đây là một dữ liệu mở rộng (additional associated data) mong muốn được xác thực nhưng không cần phải mã hóa. Có thể có nhiều dữ liệu mở rộng trong một process.

Nếu áp dụng GCM cho truyền dữ liệu internet, Auth data có thể bao gồm thông tin IP của người gửi, IP người nhận, Port người gửi, Port người nhận,v.v.

Chính vì có thêm additional associated data nên ngoài cung cấp authenticated encryption (AE) thì GCM còn cung cấp tính năng xác thực với dữ liệu bổ xung, được gọi là authenticated encryption with associated data hay AEAD.

Mult H

Đây là phép nhân với H trong trường Galois, phép nhân sẽ được giải thích trong phần bên dưới, còn giá trị H được tính như sau:

// 0^128 nghĩa là một chuỗi bit có 128 bit 0 đó.
H = E(K, 0^128)

Như thế H chính là sử dụng Ek mã hóa dữ liệu với toàn giá trị 0.

len(A) || len(C)

Đầu tiên nói về phép toán len(), phép toán này trả về một chuỗi 64bit biểu diễn thông tin độ dài của biến. Ví dụ len(A) = 001110111...01 (dài 64bit) và len(C)=000000011..100 (dài 64bit) thì hai thằng này nối với nhau sẽ thành len(A) || len(C) = 001110111...01000000011..100 (dài 64+64=128bit).

Decryption

Đã xong về encryption, còn về quá trình decryption chúng ta làm ngược lại như sau:

Khi So sánh Auth Tag của quá trình decryption với Auth Tag được gửi kèm theo ciphertext, chúng ta đã xác thực được dữ liệu rồi. Vì vậy ở đây Auth Tag đóng vai trò là một MAC đó.

GF multiplication

Phần cuối cùng ta cùng tìm hiểu về phép nhân trong trường Galois, ngôi sao của chúng ta. Với GCM cho thuật toán mã hóa đối xứng với đầu vào là 128 bit thì chúng ta sẽ thực hiện phép nhân trong trường Galois 2^128^ hay GF(2^128^)

Ví dụ ta muốn nhân hai vector bit với độ dài là 128 là X và Y. Ta ký hiệu Bit thứ i trong vector X được gọi là Xi, bit bên trái cùng của X là X0 và bit bên phải cùng của X là X127. Tương tự với Y.

Phép nhân X và Y trong $GF(2^{128})$ sử dụng một hằng số đặc biệt R được định nghĩa như sau: $R = 11100001||0^{120}$ tức là nối giữa 11100001 và 120 bit 0 đằng sau đó.

Chúng ta cùng đến với thuật toán như sau:

Nhân hai số X và Y trong GF(2^128).
Tính Z = X - Y , trong đó X, Y và Z ∈ GF(2^128)
rightshift là phép toán dịch phải một bit: rightshift(11111111) = 01111111
⊕ là phép XOR
---------------------
Z ← 0, V ← X
for i = 0 to 127 do if Yi = 1 then Z ← Z ⊕ V end if if V127 = 0 then V ← rightshift(V) else V ← rightshift(V) ⊕ R end if
end for
return Z

Các bạn có thể tìm hiểu thêm về các phép toán trong Galois Field tại một video rất hay này
https://www.youtube.com/watch?v=oPjkfvuqqv4&ab_channel=BillBuchananOBE

Hoặc có thể đọc thêm về trường Galois tại đây

https://en.wikipedia.org/wiki/Finite_field#:~:text=In mathematics%2C a finite field,and satisfy certain basic rules.

Phép tính trong trường Galois Field có thể xem trực quan bằng tool sau:

https://www.walter-fendt.de/html5/men/calculatorgaloisfield_en.htm

Kết bài

Wow, chúng ta đã xong về Block cipher mode of operation rồi, quả là một bầu trời kiến thức phải không nào, nếu đọc sâu học toán chết bà luôn 🤣. Nhưng dù sao thì nếu bạn đọc từ đầu tới đây chắc hẳn là đã mường tượng ra được người ta mã hóa kiểu gì rồi phải không nào. Bài này tới đây là hết, các bạn cùng đón đọc bài tiếp theo nhé.

References & Tools

Bài viết gốc:

[Cryptography p13] Block cipher mode of operation

Mở bài

Block cipher mode of operation

Electronic codebook (ECB)

Cipher block chaining (CBC)

Counter (CTR)

MAC

GCM

Encryption

Counter

Ek

Phép ⊕

Auth data 1

Mult H

len(A) || len(C)

Decryption

GF multiplication

Kết bài

References & Tools

Bình luận

Bài viết tương tự

Tìm hiểu mã hóa, giải mã, các thuật toán mã hóa - Phần 2 - Demo thuật toán mã hóa AES

Mã hóa đối xứng - Phần 1: Feistel và DES

Giới thiệu về kĩ thuật tấn công AES-ECB Oracle

Symmetric ciphers - Mật mã đối xứng AES (phần 4)

Symmetric ciphers - Mật mã đối xứng AES (phần 5)

Symmetric ciphers - Mật mã đối xứng AES (phần 7)