Bài viết được lấy từ https://truongphuoc.wordpress.com/2023/02/21/blockchain-15-he-mat-doi-xung/
Chào các bạn, trong bài trước mình đã trình bày về mật mã học cơ bản. Chúng ta đã biết mã hóa được chia thành hệ mật đối xứng và hệ mật bất đối xứng. Hôm nay chúng ta cùng tìm hiểu về hệ mật đối xứng và một vài thuật toán thuộc loại này nhé.
Mã hóa đối xứng
Trong mã hóa đối xứng, quá trình Encypt và Decrypt đều sử dụng chung một mã.
Ví dụ với thuật toán Ceacar, với việc chọn Key = 3, khi Encypt ta phải dịch chuyển từng ký tự sang phải 3 đơn vị. Đồng thời khi Decrypt ta cũng phải dịch chuyển sang trái 3 đơn vị. Nếu chuyển sang trái 2 đơn vị thì sẽ giải sai mã.
Mã hóa đối xứng được chia thành hai nhóm nhỏ là:
- Thuật toán mã hóa theo khối (Block ciphers): Dữ liệu sẽ được chia thành các khối bit, thuật toán sẽ mã hóa theo từng khối bit một.
- Thuật toán mã hóa theo dòng (Stream ciphers): Dữ liệu sẽ được mã hóa theo từng bit một.
Trong bài viết này mình sẽ giới thiệu về thuật toán mã hóa đối xứng với AES.
Trước khi vào chi tiết về thuật toán AES, mình xin nói một chút về thuật toán DES (Data Encryption Standard). Đây là thuật toán có trước AES, được sử dụng vào những năm 1977 đến 1997. Nhưng sau đó dưới sự phát triển mạnh mẽ của khả năng tính toán của máy tính, thuật toán này bộc lộ nhiều yếu điểm. Nên nó ít được sử dụng đi và nhường chỗ cho thuật toán mới hơn, mạnh mẽ hơn AES.
Chú ý kẻo ngợp: Bài viết nặng về tính toán, tuy tính toán đơn giản nhưng lại nhiều. Các bạn cố gắng đọc hết để hiểu thuật toán nhé. Mình viết hơi dài dòng một chút nhưng chi tiết để mọi người cùng nắm được nội dung.
AES (Advandge Encryption Standard)
AES là một thuật toán mã hóa khối (đầu vào được chia thành các khối với giá trị từng khối là 128 bits dữ liệu). AES có thể có các độ dài khóa là 128 bits (AES-128), 192 bits (AES-192) và 256 bits (AES-256). Quá trình Encryption và Decryption của AES như sau:
Trong hình trên, với quá trình Encryption, ta lặp đi lặp lại quá trình Encryption Round (khối xanh phái trên) với Nr-1 lần, sau đó chạy qua Last Round (khối xanh phía dưới), ta được bản Cypher text.
Còn với quá trình Decryption, ta lại làm ngược lại, ta lặp lại quá trình Decryption Round (khối xanh ở dưới) với Nr-1 lần, sau đó chạy qua Last Round (khối xanh ở trên) để ra được Plain text. Các function trong quá trình Decryption ngược (inverse) với các function trong quá trình Encryption.
Nr là số vòng lặp được xác định dựa trên Key lengh (độ dài khóa) với AES-128 thì Nr = 10, AES-192 thì Nr = 12 và với AES-256 thì Nr = 14.
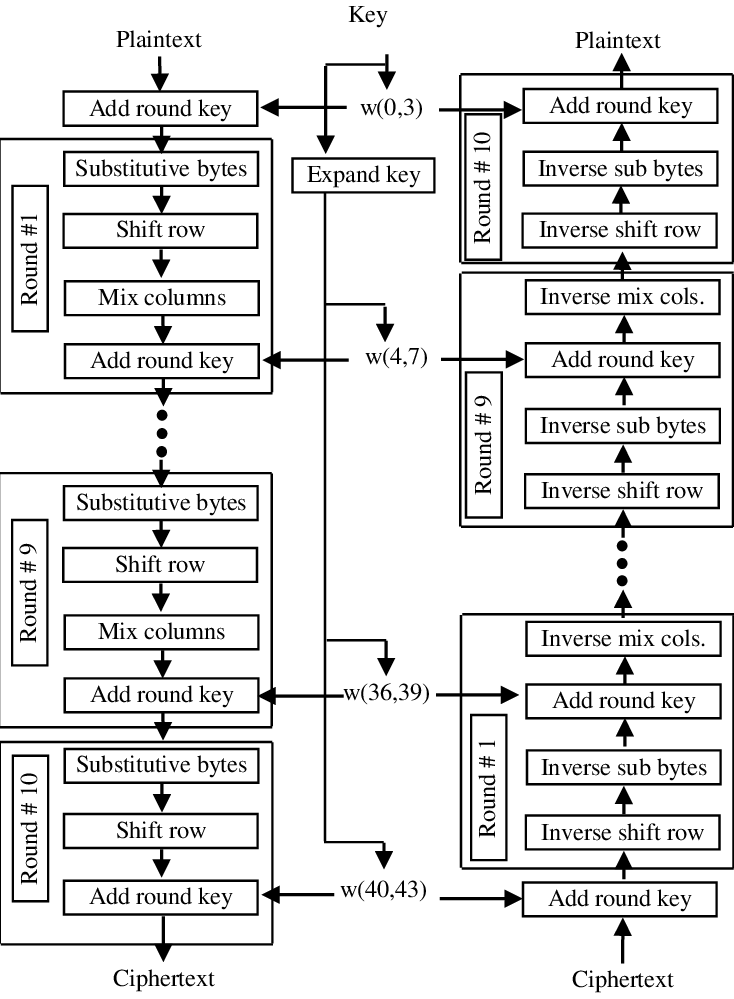
Một bản chi tiết hơn quá trình Encryption và Decryption của AES-128
Chúng ta cùng tìm hiểu kỹ hơn về các thành phần trong hệ mã AES-128 nhé.
Đầu vào
AES là thuật toán mã hóa khối, với các khối có giá trị 128 bits. Nên đầu vào của thuật toán này là một khối 128 bits. Ví dụ với Plain text là: "se co thien than thay anh yeu em" được chuyển sang hệ nhị phân sử dụng mã encoding là ASCII sẽ có giá trị như sau:
01110011 01100101 00100000 01100011 01101111 00100000 01110100 01101000 01101001 01100101 01101110 00100000 01110100 01101000 01100001 01101110 00100000 01110100 01101000 01100001 01111001 00100000 01100001 01101110 01101000 00100000 01111001 01100101 01110101 00100000 01100101 01101101
Giá trị ở trên là 256 bits, nhưng thuật toán AES nhận giá trị đầu vào là 128 bits. Cho nên chúng ta tách dãy bit trên thành 2 phần như sau:
Phần 1
01110011 01100101 00100000 01100011 01101111 00100000 01110100 01101000 01101001 01100101 01101110 00100000 01110100 01101000 01100001 01101110
Phần 2
00100000 01110100 01101000 01100001 01111001 00100000 01100001 01101110 01101000 00100000 01111001 01100101 01110101 00100000 01100101 01101101
Giả sử đầu vào không đủ 128 bits, chúng ta sẽ thêm các bit 0 vào sau để có thể đủ 128 bits cho dữ liệu đầu vào.
Nhìn phần 1 toàn 0 và 1 chúng ta khó tính toán, dễ sai lầm, mình sẽ chuyển từ hệ cơ số 2 sang cơ số 16 cho dễ dàng hơn nhé.
Ta chuyển 01110011 từ cơ số 2 thành 73 ở cơ số 16, 01100101 từ cơ số 2 thành 65 ở cơ số 16, và cứ như thế phần 1 trên trở thành:
73 65 20 63 6F 20 74 68 69 65 6E 20 74 68 61 6E
Mình làm ví dụ chơi chơi vậy thôi, chứ mình bên dưới khi đi sâu vào từng function trong AES mình sẽ lấy ví dụ sau để làm:
19 3d e3 be a0 f4 e2 2b 9a c6 8d 2a e9 f8 48 08
Do lười tính toán nên mình lấy ví dụ trên mạng cho đỡ phải tính ấy mà 🤣. Nhưng các bạn yên tâm, mình sẽ giải thích tường tận để tính toán trong từng bước nhé.
SubBytes()
Hàm SubBytes thực hiện phép thay thế các byte của mảng ttrạng thái bằng cách sử dụng S-box.
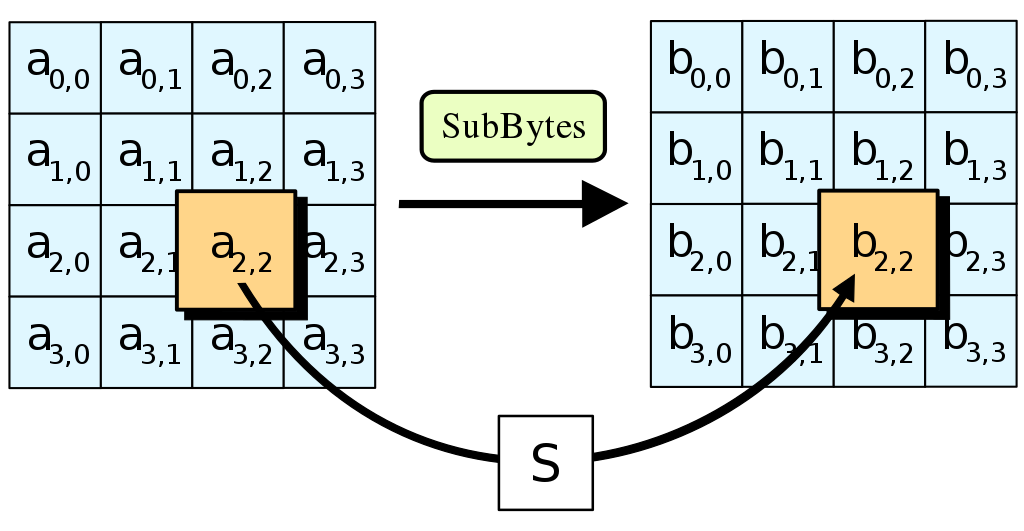
Các bit đầu vào được chia thành 4 hàng, với mỗi hàng có 4 khối. Tại vì đầu vào là 128 bits nên mỗi hàng có 128/4 = 32 bits, mỗi khối là 32/4 = 8 bits, tương ứng với 1 byte.Với ví dụ trên, ta có thể viết lại như sau:
19 a0 9a e9
3d f4 c6 f8
e3 e2 8d 48
be 2b 2a 08
(Chú ý là sắp xếp theo cột trước hàng sau nhé các bạn)
Ứng với mỗi khối này ta sẽ đối chiếu với bàng S-box để trả về kết quả.
| 00 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 0a | 0b | 0c | 0d | 0e | 0f | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 63 | 7c | 77 | 7b | f2 | 6b | 6f | c5 | 30 | 01 | 67 | 2b | fe | d7 | ab | 76 |
| 10 | ca | 82 | c9 | 7d | fa | 59 | 47 | f0 | ad | d4 | a2 | af | 9c | a4 | 72 | c0 |
| 20 | b7 | fd | 93 | 26 | 36 | 3f | f7 | cc | 34 | a5 | e5 | f1 | 71 | d8 | 31 | 15 |
| 30 | 04 | c7 | 23 | c3 | 18 | 96 | 05 | 9a | 07 | 12 | 80 | e2 | eb | 27 | b2 | 75 |
| 40 | 09 | 83 | 2c | 1a | 1b | 6e | 5a | a0 | 52 | 3b | d6 | b3 | 29 | e3 | 2f | 84 |
| 50 | 53 | d1 | 00 | ed | 20 | fc | b1 | 5b | 6a | cb | be | 39 | 4a | 4c | 58 | cf |
| 60 | d0 | ef | aa | fb | 43 | 4d | 33 | 85 | 45 | f9 | 02 | 7f | 50 | 3c | 9f | a8 |
| 70 | 51 | a3 | 40 | 8f | 92 | 9d | 38 | f5 | bc | b6 | da | 21 | 10 | ff | f3 | d2 |
| 80 | cd | 0c | 13 | ec | 5f | 97 | 44 | 17 | c4 | a7 | 7e | 3d | 64 | 5d | 19 | 73 |
| 90 | 60 | 81 | 4f | dc | 22 | 2a | 90 | 88 | 46 | ee | b8 | 14 | de | 5e | 0b | db |
| a0 | e0 | 32 | 3a | 0a | 49 | 06 | 24 | 5c | c2 | d3 | ac | 62 | 91 | 95 | e4 | 79 |
| b0 | e7 | c8 | 37 | 6d | 8d | d5 | 4e | a9 | 6c | 56 | f4 | ea | 65 | 7a | ae | 08 |
| c0 | ba | 78 | 25 | 2e | 1c | a6 | b4 | c6 | e8 | dd | 74 | 1f | 4b | bd | 8b | 8a |
| d0 | 70 | 3e | b5 | 66 | 48 | 03 | f6 | 0e | 61 | 35 | 57 | b9 | 86 | c1 | 1d | 9e |
| e0 | e1 | f8 | 98 | 11 | 69 | d9 | 8e | 94 | 9b | 1e | 87 | e9 | ce | 55 | 28 | df |
| f0 | 8c | a1 | 89 | 0d | bf | e6 | 42 | 68 | 41 | 99 | 2d | 0f | b0 | 54 | bb | 16 |
Bảng S-box
Với số đầu tiên 19 ta tìm trong bảng S-box hàng 1 cột 9, ta được giá trị là d4, thay 19 thành d4. Với số thứ hai là a0 ta tìm hàng a cột 0 được giá trị e0, thay a0 thành e0. Và cứ như thế ta có bảng sau khi sub byte như sau:
d4 e0 b8 1e
27 bf b4 41
11 98 5d 52
ae f1 e5 30
ShiftRows()
Áp dụng lên mảng trạng thái bằng cách dịch vòng các hàng của mảng trạng thái với số lần dịch khác nhau. Hàng đầu tiên chúng ta giữ nguyên, hàng thứ 2 dịch sang trái một khối, hàng thứ 3 dịch sang trái hai khối, hàng thứ 4 dịch sang trái 3 khối.
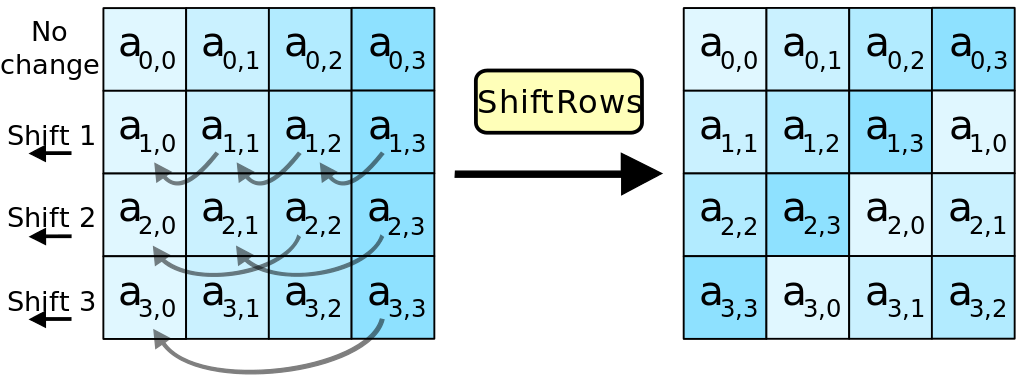
Với kết quả SubBytes() trên ta dịch như sau:
- Hàng đầu giữ nguyên: d4 e0 b8 1e
- Hàng hai dịch sang trái một khối: 27 bf b4 41 => bf b4 41 27
- Hàng ba dịch sang trái hai khối: 11 98 5d 52 => 5d 52 11 98
- Hàng tư dịch sang trái ba khối: ae f1 e5 30 => 30 ae f1 e5
Ta có kết quả như sau:
d4 e0 b8 1e
bf b4 41 27
5d 52 11 98
30 ae f1 e5
MixColumns()
Làm việc trên các cột của mảng trạng thái. Các cột được coi như là đa thức trong trường GF(2^8^) và nhân với một đa thức a(x) với a(x) = 3x^3^ + x^2^ + x +2.
A(x) có thể triển khai thành ma trận:

Nghe có vẻ loàng ngoàng nhưng ta sẽ làm như sau: Nhân ma trận trên với mảng trạng thái, ta sẽ ra được kết quả

Đây là phép toán nhân ma trận, ta sẽ tính từ phần tử nhé.
S00 = 02*d4 + 03*bf + 01*5d + 01*30 S01 = 02*e0 + 03*b4 + 01*52 + 01*ae S11 = 01*e0 + 02*b4 + 03*52 + 01*ae ....
Ta tính toán S00 như sau:
Để dễ dàng trình bày hơn, x^7 mình sẽ viết thành x7, x^6 mình sẽ viết thành x6,... Đặt x = 2
d4 = 1101.0100
2*d4 = 1.1010.1000
(Phép nhân 2 trong binary thực chất là phép dịch trái 1 bit, ta dịch 8f sang trái 1 bit, không tin bạn cứ làm thử 0000.0010 * 1000.1111 xem có ra kết quả này không :) ). Ta thấy 2*d4 > 2^8
=> Ta cần mod 2*d4 cho đa thức x8 + x4 + x3 + x + 1 (1) Trong GF(2^8) phép mod này tương đương với phép ⊕1.0001.1011 (Phép XOR bit nhé). Ai quên thì XOR như sau: 1 ⊕ 1 = 0, 1 ⊕ 0 = 1, 0 ⊕ 1 = 1, 0 ⊕ 0 = 0 (Chú ý: chỉ mod nếu giá trị > 2^8, nếu <= 2^8 thì thôi khỏi mod làm gì nhé). 1.1010.1000 ⊕ 1.0001.1011 = 0.1011.0011 = 1011.0011
Do đó 2*d4 = 1011.0011
----
3*bf = bf ⊕ 2*bf
bf = 10111111
2*bf = 1.0111.1110
bf ⊕ 2*bf = 0.1011.1111 ⊕ 1.0111.1110 = 1.1100.0001 > 2^8 => Cần mod cho đa thức (1)
1.1100.0001 ⊕ 1.0001.1011 = 0.1101.1010 = 1101.1010
Do đó 3*bf = 1101.1010
----
1*5d = 5d = 0101.1101
----
1*30 = 30 = 0011.0000
----
2*d4 + 3*bf + 1*5d + 1*30
= 1011.0011 ⊕ 1101.1010 ⊕ 0101.1101 ⊕ 0011.0000
= 0110.1001 ⊕ 0101.1101 ⊕ 0011.0000
= 0011.0100 ⊕ 0011.0000
= 0000.0100 Chuyển sang dạng hex thì 0000.0100 = 04
Do đó 2*d4 + 3*bf + 1*5d + 1*30 = 04 tức S00 của chúng ta là 04 Phù hơi mệt :)
Làm các phép toán tương tự với các phần tử S01, S02,...S33. Sau khi tính toán xong ta được kết quả như sau:
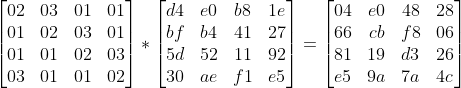
AddRoundKey()
Mảng trạng thái sẽ được cộng với một round key (khóa vòng) bằng một thao tác XOR bit.
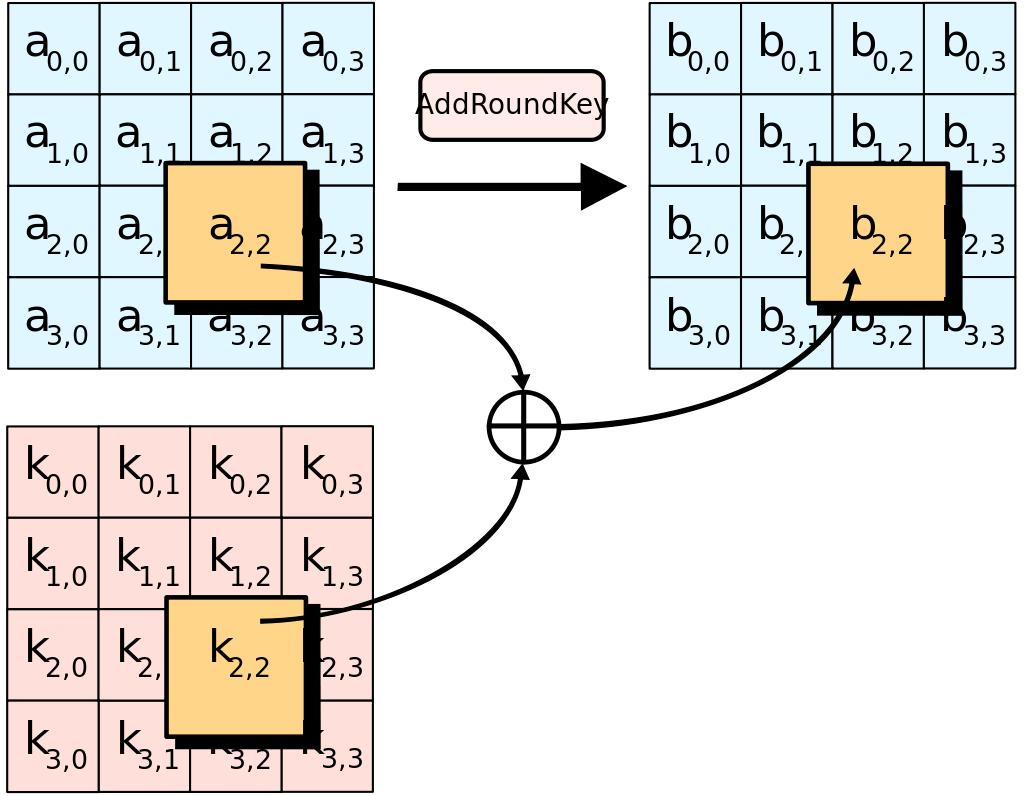
Round key là gì? AES là hệ mật đối xứng nên sẽ có một Key vừa dùng để mã hóa vừa dùng để giải mã. Key này sẽ được phân tách ra thành các Round key để phục vụ cho việc chạy lặp lại trong lúc mã hóa và giải mã. Cách tạo Round key chúng ta cùng tìm hiểu bên dưới nhé. Hiện tại chỉ cần biết rằng Key sẽ được tách thành các Round key, mỗi Round key có độ dài là 128 bits.
AddRoundKey() function khá dễ dàng. Ví dụ với Round Key là:
a0 88 23 2a
fa 54 a3 6c
fe 2c 39 76
17 b1 39 05
Ta có kết quả như sau:

Cách tính như sau:
04 ⊕ a0 = 0000.0100 ⊕ 1010.0000 = 1010.0100 = a4
e0 ⊕ 88 = 1110.0000 ⊕ 1000.1000 = 0110.1000 = 68
....
Tương tự với các trường hợp còn lại.
Thế là mình đã xong các function trong quá trình Encryption. Tiếp theo chúng ta cùng tìm hiểu thuật toán để sinh Round key nhé.
Key expansion

Quá trình tạo khóa con mở rộng
Khóa đầu vào được sắp xếp thành một ma trận. Ví dụ mình có khóa đầu vào như sau:
2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c
Ta sắp xếp khóa này thành ma trận như sau:
ae b5 31 7f
d2 8d 2b 8d
73 ba f5 29
21 d2 60 2f
| | | |
w0 w1 w2 w3
Ta đặt từng cột của ma trận trên là w0, w1, w2, w3 như trên. Theo như biểu đồ chu trình trên thì:
w4 = g ⊕ w0 w5 = w4 ⊕ w1 w6 = w5 ⊕ w2 ... w8 = g ⊕ w4 ...
Và cứ như thế cho đến khi kết thúc.
Thế nên mấu chốt ta phải tính được w4. Mà w4 = w3 đi qua g. Ta cùng xem xét g.
g gồm 3 thành phần con: RotWord(), SubBytes(), Rcon. Chúng ta cùng tìm hiểu chi tiết các function này.
RotWord()
Đây là phép toán dịch trái 1 byte. Với ví dụ w3 như trên ta tính như sau:
w3 = 7f 8d 29 2f
RotWord() // Chuyển 7f xuống cuối, ta được:
w'3 = 8d 29 2f 7f
SubBytes()
Giống với SubBytes() mình đã giới thiệu ở trên, tra trong bảng S-box để thay thế kết quả, với kết quả RotWord() phần trên ta có ví dụ sau:
w'3 = 8d 29 2f 7f
SubByte() // Tra trong bảng S-box để thay thế từng byte của w'3, ta được:
w''3 = 5d a5 15 d2
Rcon
Thực hiện phép XOR với RCon
Rcon được định nghĩa như sau: Rcon[i] chứa các giá trị nhận bới với i là số vòng lặp.
Ví dụ với vòng lặp đầu tiên: i = 0 => Rcon[0] = // Vì
Với vòng lặp thứ hai: i = 1 => Rcon[1] = // Vì
Tương tự với các trường hợp khác.
Với w''3 ở trên, ta đang ở vòng lặp đầu tiên => Rcon[0] = {01}, {00}, {00}, {00}. Ta làm như sau:
w''3 = 5d a5 15 d2
w'''3 = w''3 ⊕ Rcon[0] = 5d a5 15 d2 ⊕ 01 00 00 00 = 5c a5 15 d2
Đến đây ta đã có được kết quả đầu ra của w3 qua g là w'''3. Để tính w4 ta chỉ việc tính w0 ⊕ w'''3 là được.
w'''3 = 5c a5 15 d2
w0 = ae d2 73 21
w'''3 ⊕ w0 = 5c a5 15 d2 ⊕ ae d2 73 21 = f2 77 66 f3
Vậy ta được w4 = f2 77 66 f3, tiếp theo tính w5. W5 = w1 ⊕ w4
w1 = b5 8d ba d2
w4 = f2 77 66 f3
w1 ⊕ w4 = b5 8d ba d2 ⊕ f2 77 66 f3 = 47 fa dc 21
Vậy w5 = 47 fa dc 21. Với các w khác ta tính tương tự. Thế là ta đã có Round key để sử dụng rồi.
Như thế mình đã trình bày xong về hệ mã đối xứng và thuật toán mã hóa AES. Ở đây mình chỉ nói về thuật toán mã hóa, còn giải mã thì các bạn làm ngược lại với quá trình mã hóa, các bạn đi đường nào thì về ngược lại của đường đó là được thôi, đúng không.
Bài viết đến đây là hết rồi, trong bài tiếp theo mình sẽ trình bày về hệ mật bất đối xứng nhé.
Link bài viết gốc: https://truongphuoc.wordpress.com/2023/02/21/blockchain-15-he-mat-doi-xung/