Distance Measure trong Machine learning

Introduction

Distance measures hay còn được biết đến là các phương pháp tính khoảng cách (point vs point, vector vs vector...) Các phương pháp này rất thường xuyên được sử dụng trong thuật toán như k-NN, UMAP, DBSCAN...

Tuy nhiên mỗi method có các ưu điểm cũng như nhược điểm riêng, việc lựa chọn distance measure tốt có thể giúp mô hình trở nên robust hơn. Hãy cùng tìm hiểu các phương pháp phổ biến thường được sử dụng trong bài viết này nhé. Let's go

1. Euclidean Distance

Có lẽ đây là phương pháp phổ biến nhất vì ai cũng đã phải học từ thời cấp 2 :v. Euclidean Distance còn được biết đến với cái tên $L_2$ distance.

$D(x, y) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$

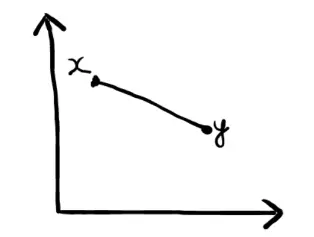
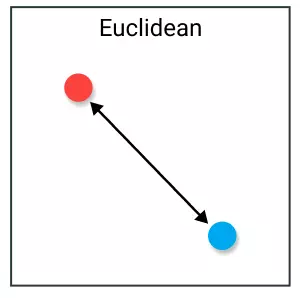
Cách tính toán không có gì phức tạp, tính căn bậc hai tổng bình phương hiệu của các điểm.

Ưu:

• Phổ biến, dễ hiểu, dễ implement, kết quả tốt trong nhiều usecase
• Đặc biệt hiệu quả với dữ liệu ít chiều,

Nhược điểm:

• Euclide distance có thể bị ảnh hưởng bởi đơn vị của feature. Chính vì vậy cần phải normalize trước khi tính toán
• Vấn đề thứ 2, khi số chiều vector space tăng lên, Euclide Distance trở nên kém hiệu quả. Một phần nguyên nhân do dữ liệu thực tế thường không chỉ nằm trong Euclide Metric Space. Cụ thể hơn có thể tham khảo tại đây

2. Manhattan Distance

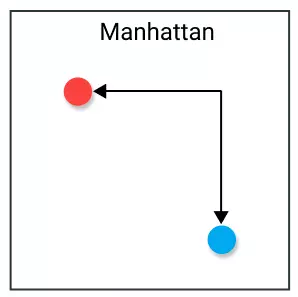
Hay còn gọi là khoảng cách $L_1$ (hay Taxicab/City Block distance)

Để so sánh với Euclide Distance thì có thể hiểu trên map Euclide Distance là đường chim bay (màu đỏ) còn Manhattan là đường bộ (màu xanh) theo các block nhà :v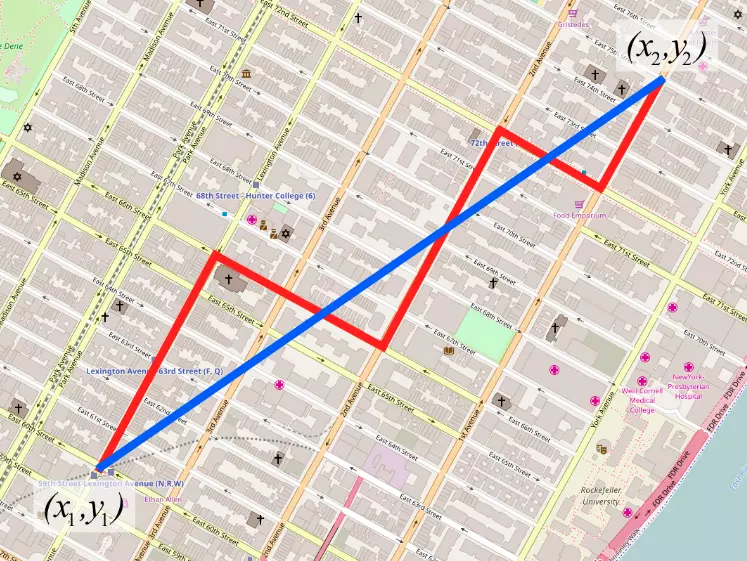

$D(x, y) = \sum_{i=1}^k |x_i - y_i|$

Một biến thể khác của Manhattan Distance là Canberra distance

$D(x, y) = \sum_{i=1}^n \frac{|x_i - y_i|}{|x_i| + |y_i|}$

Phương pháp này tương tự với $L_1$ khoảng cách Manhattan tuy nhiên giá trị về độ lớn của các vector được tận dụng. Ngoài ra Mahattan Distance cũng được sử dụng như string metric (so sánh string)

3. Chebyshev Distance

Khoảng cách Chebyshev tính toán đơn giản hơn, tính độ lệch lớn nhất của 2 vector theo trục tọa độ. Còn được biết đến với tên gọi khoảng cách Chessboard

$D(x, y) = \max_{i} (|x_i - y_i|)$

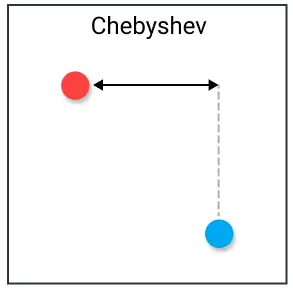
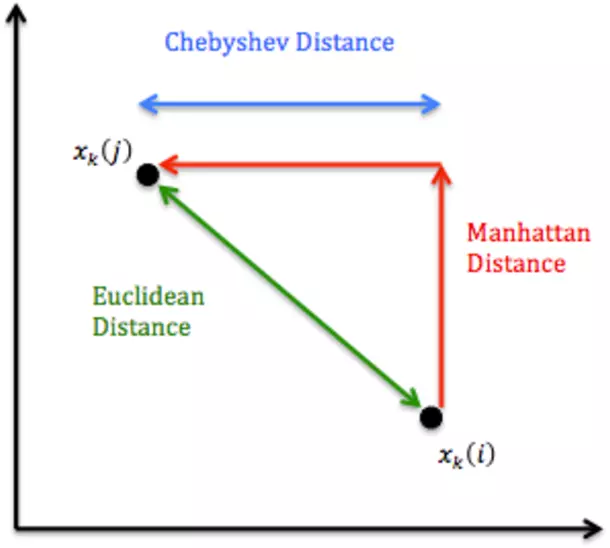
Hình so sánh với 2 metric trên

Nhược điểm:

• Chỉ tốt với vài trường hợp cụ thể do không có tính generalize tốt như các phương pháp khác như Euclidean hay Cosine similarity.

Use Case:

• Đặc điểm của measrue này cho phép tính được số bước đi tối thiểu từ ô này sang ô khác. Nên có thể có lợi trong các trò chơi, game cho phép di chuyển 8 hướng.
• Trong thực tế Chebyshev distance thường được sử dụng trong warehouse logistics (điều khiển cần trục di chuyển)

4. Minkowski

Hay còn gọi là p-norm vector

$D(x, y) = (\sum_{i=1}^n |x_i - y_i|^p)^{\frac{1}{p}}$

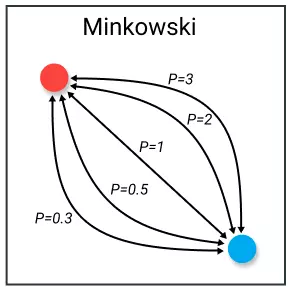
Có thể thấy Minkowski distance là trường hợp tổng quát của các distance bên

• p = 1 => Manhattan distance
• p = 2 => Euclidean distance
• p = $\infin$ => Chebyshev distance

Nhược điểm:

• Minkowski có các nhược điểm tương tự các phương pháp kể trên. Tham số $p$ có thể cần phải điều chỉnh rất nhiều để tìm được giá trị phù hợp

Use case:

• Việc có thể chọn lựa tham số $p$ thích hợp giúp việc điều chỉnh mô hình trở nên linh họat hơn

5. Cosine Similarity

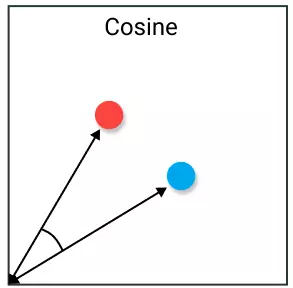
Cosine similarity thường được sử dụng để giải quyết vấn đề của Euclidean distance ở không gian nhiều chiều. Ý tưởng đơn giản là tính góc tạo thành giữa 2 vector. Giá trị sẽ tương đương với phép dot product nếu cả 2 vector được norm về giá trị 1.

2 vecor cùng hướng sẽ có cosine similarity bằng 1 và ngược hướng sẽ có giá trị -1. Lưu ý rằng, chiều dài không được sử dụng do đây là phương pháp tính theo hướng.

$D(x, y) = cos(\theta) = \frac{x \cdot y}{||x|| ||y||}$

Nhược điểm:

• Không tận dụng độ lớn của vector, chỉ tính theo hướng
• Điều này vô tình làm mất mát thông tin so sánh

Use case: Thường được sử dụng trong các dữ liệu đa chiều và không quá phụ thuộc vào độ lớn của vector.

6. Hamming Distance

Đây là string metric

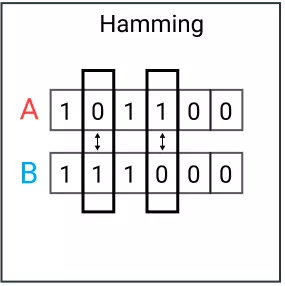
Khoảng cách Hamming là số giá trị khác nhau giữa 2 vector. Phương pháp này thường được dùng để so sánh 2 chuỗi binary có độ dài bằng nhau. Phương pháp này cũng có thể so sánh độ tương đồng của vector bằng cách tính số lượng ký tự khác nhau.

Nhược điểm:

• Khoảng cách Hamming khó áp dụng với 2 vector có số chiều không tương đồng
• Phương pháp này sẽ không tính các giá trị khác nhau của 2 vector, nên thường không sử dụng khi độ lớn là yếu tố cần thiết

Use case:

• Tính distance các biến dạng categorical
• Dùng để phát hiện/sửa các bit nhiễu khi truyền dữ liệu trong mạng máy tính

7. Leveshtein Distance

Đây cũng là một string metric

${\displaystyle \qquad \operatorname {lev} (a,b)={\begin{cases}|a|&{\text{ if }}|b|=0,\\|b|&{\text{ if }}|a|=0,\\\operatorname {lev} (\operatorname {tail} (a),\operatorname {tail} (b))&{\text{ if }}a[0]=b[0]\\1+\min {\begin{cases}\operatorname {lev} (\operatorname {tail} (a),b)\\\operatorname {lev} (a,\operatorname {tail} (b))\\\operatorname {lev} (\operatorname {tail} (a),\operatorname {tail} (b))\\\end{cases}}&{\text{ otherwise.}}\end{cases}}}$

trong đó $tail(x)$ là chuỗi bắt đầu từ $x$ và x\[x\] là ký tự thứ $n$ của chuỗi $x$ (tính từ 0).

Khoảng cách này được đặt theo tên Vladimir Levenshtein từ năm 1965. Thường được sử dụng trong việc tính toán sự giống và khác nhau giữa 2 string, như chương trình kiểm tra lỗi chính tả của winword spellchecker.

Ví dụ: Khoảng cách Levenshtein giữa 2 chuỗi "kitten" và "sitting" là 3, vì phải dùng ít nhất 3 lần biến đổi.

kitten -> sitten (thay "k" bằng "s")

sitten -> sittin (thay "e" bằng "i")

sittin -> sitting (thêm ký tự "g")

8. Jaccard Index

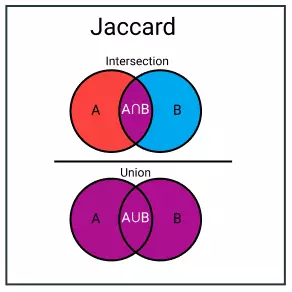
Hay còn được biết đến với cái tên Intersection over Union (IoU), có lẽ đã quá quen với các bài toán Object Detection. Là metric tính toán sự tương đồng và đa dạng của tập mẫu. Trong thực tế, chỉ số này đại diện cho tỉ lệ giữa dữ liệu chung chia tổng dữ liệu.

Jaccard Index

$J(x, y) = \frac{|x \cap y|}{|y \cup x|}$

Jaccard Distance

$D(x, y) = 1 - \frac{|x \cap y|}{|y \cup x|}$

Một bức hình quen thuộc hơn với các anh em nghiên cứu về Object Detection trong CV task

Nhược điểm:

• Phụ thuộc nhiều vào kích thước của dữ liệu. Bộ dataset lớn thì Union cũng tăng theo

Use case:

• Image Segmentation (IoU)

Ngoài ra trong nghiên cứu này cho thấy Jaccard index hoạt động kém hiệu quả với dữ liệu thực hoặc các bài dạng weighted set (cover set). Nên nhóm tác giả đã đề xuất Generalized Jaccard có thay đổi một chút

$D(x, y) = \frac{\sum_i \min(x_i, y_i)}{\sum_i \max(x_i, y_i)}$

Paper cũng chỉ thực hiện so sánh giữa các phương pháp tương tự bao gồm Jaccard index, Generalized Jaccard và Sørensen-Dice

Giờ đến các distance ít phổ biến hơn một chút

9. Sørensen-Dice Index

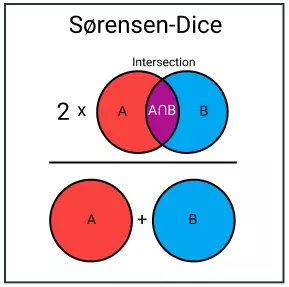
Phương này khá tương tự Jaccard Index về tính độ tương đồng. Điểm khác biệt có thể hiểu là Sørensen-Dice tính độ tính tỉ lệ độ trùng lặp giữa 2 set. Tỉ lệ này sẽ luôn nằm giữa 0 và 1.

$D(x, y) = \frac{2 |x+y|}{|x|+|y|}$

Nhược điểm:

• Giống như Jaccard index, metric này sẽ chút trọng vào các tập có ít/không có groundtruth. Việc dẫn đến việc mất cân bằng giữa các tập có giao điểm và không có giao điểm.

Use case:

• Cũng gần giống Jaccard Index, thường sử dụng trong các bài image segmentaiton hay phân tích text similarity

10. Haversine

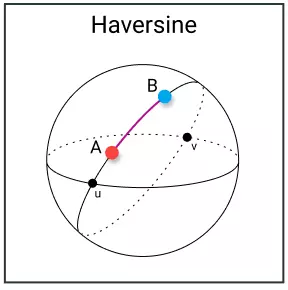
Đây là khoảng cách giữa 2 điểm trên khối hình cầu. Cách tính toán có phần tương tự như khoảng cáchEuclidean, tính khoảng cách ngắn nhất giữa 2 điểm. Điểm khác biệt có lẽ là 2 điểm này nằm trên khối cầu => khoảng cách là cung nhỏ nhất nối 2 điểm

$d = 2r\arcsin(\sqrt{\sin^2{(\frac{\varphi_2 - \varphi_1}{2}})+\cos{\varphi_1}\cos{\varphi_2}\sin^2{(\frac{\lambda_2 - \lambda_1}{2})}})$

Nhược điểm:

• Vector space phải chuẩn hình cầu. Trong thực tế việc này khó xảy ra

Use case:

• Phù hợp với các bài toán cần tình toán trên hình cầu đường cong lớn (nếu không thì đường cong không đóng góp nhiều ý nghĩa)
• Được dùng để tính toán gần đúng khoảng cách đường hàng không giữa các quốc gia. Nhưng thực tế thì trái đất không có hình cầu nên 1 phương pháp khác cũng được sử dụng là Vincenty distance

11. Mahalanobis Distance

Đây là khoảng cách tính giữa điểm P và phân bố D (mean).

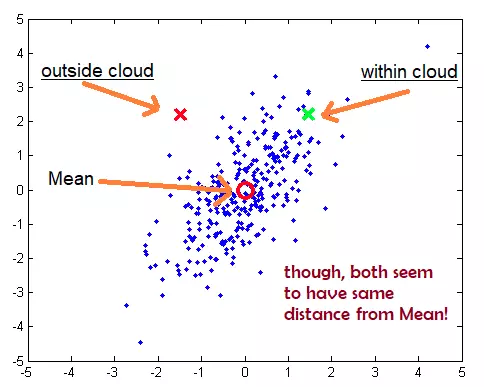
Trong dữ liệu đa biến, khoảng cách Euclidean thường không tốt nếu có sự xuất hiện covariance (hiệp phương sai) giữa các biến này

$D_M(\vec{x}) = \sqrt{(\vec{x} - \vec{\mu})^T S^{-1}(\vec{x} - \vec{\mu})}$

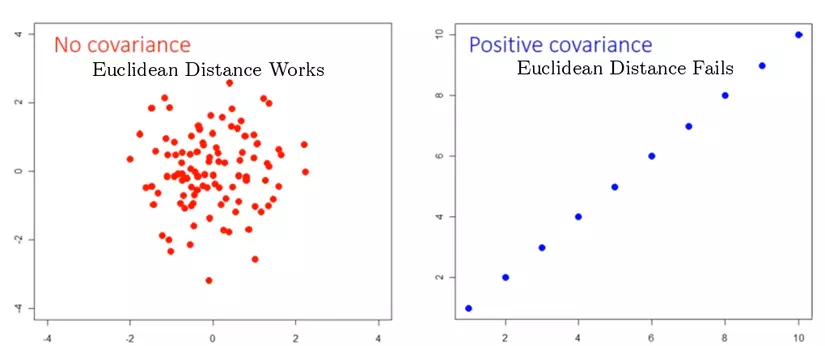
với $\mu$ là mean và $S$ là covariance matrix (ma trận hiệp phương sai)

Ngoài ra, Mahalanobis distance cũng có thể được tính giữa 2 vector với cùng phân bố ma trận $S$

$d(\vec{x}, \vec{y}) = \sqrt{(\vec{x} - \vec{y})^T S^{-1}(\vec{x} - \vec{y})}$

Trường hợp dặc biệt của Mahalanobis: Nếu ma trận $S$ là ma trận đơn vị, Mahalanobis distance trở thành Euclidean distance. Trường hợp $S$ là ma trận chéo thì kết quả thu được là Euclidean distance chuẩn hóa

${\displaystyle d({\vec {x}},{\vec {y}})={\sqrt {\sum _{i=1}^{N}{\frac {(x_{i}-y_{i})^{2}}{s_{i}^{2}}}}},}$

12. Bray-Curtis distance & KL-divergence

Phương pháp này xin phép trích dẫn một bài của tác giả khác khá hay và cụ thể

Entropy, cross entropy va KL Divergence - Nguyen Thanh Trung

Bray Curtis dissimilarity Wiki

Kết

Trên đây là overview một vài distance measurement thường được sử dụng. Ngoài ra còn một số phương pháp nữa nhưng ít phổ biến hoặc mình chưa tìm hiểu nhiều nên không được đưa vào bài viết này. Bao gồm các distance như Vincenty distance, Jaro-Winkler, Hellinger distance ...

Bài viết mình có tham khảo và sưu tầm từ nhiều nguồn. Nếu có gì sai sót xin hãy góp ý ở phần comment bên dưới. Many thanks!

Xin cám ơn các bạn đã đọc bài (^^)

Rerferences

[1] 9 Distance Measures in Data Science

[2] Importance of Distance Metrics in Machine Learning Modelling

[3] Distance/Similarity Measures in Machine Learning

[4] On the Surprising Behavior of Distance Metrics in High Dimensional Space (curse of dimensionality)

[5] Mahalanobis Distance - stackoverflow, wiki, youtube

[6] 3 distances that every data scientist should know

[7] Và rất nhiều sự Google