Hãy tưởng tượng rằng Alice đã huấn luyện một mô hình học máy. Bob muốn xác minh xem liệu Alice đã thực sự huấn luyện mô hình hay chưa, nhưng Alice không muốn tiết lộ mô hình của mình (vì đây là bí mật và cô ấy muốn giữ nó riêng tư). Vì vậy, Alice muốn chứng minh cho Bob rằng cô ấy có mô hình, đồng thời không tiết lộ bất kỳ thông tin nào cho Bob?.
Câu hỏi đặt ra là Có cách nào để thực hiện kịch bản này không?
Để trả lời câu hỏi này mời mọi người xem qua 1 bài giới thiệu nhỏ về ZKML ( nhỏ vì nó chưa đầy đủ để nói về các khía cạnh của ZK vs ML )
1. Introduction
1.1 BACKGROUND ON ZERO-KNOWLEDGE PROOFS
Zero-knowledge proofs (ZKPs) là một nguyên lý mật mã cho phép người chứng minh (prover) thuyết phục người xác nhận (verifier) rằng một tuyên bố cụ thể là đúng mà không tiết lộ bất kỳ thông tin nào về tuyên bố đó. Khái niệm này được giới thiệu lần đầu tiên bởi Goldwasser, Micali và Rackoff trong bài báo của họ về các hệ thống chứng minh tương tác ( interactive proof systems). Ý tưởng cốt lõi đằng sau ZKP là xây dựng một chứng minh( proof) có thể được xác minh, trong khi không rò rỉ bất kỳ thông tin nào về dữ liệu hoặc tính toán đang diễn ra. Về mặt toán học, một ZKP có thể được biểu diễn như sau:
Cho một mối quan hệ R(x,w), ở đây x là đầu vào công khai, w là khóa bí nhật, giao thức ZKP cho phép người chứng minh (prover) thuyết phục người xác minh (verifier) rằng ∃w sao cho R(x,w) = 1 mà không tiết lộ bất kỳ thông tin nào về w. Về mặt hình thức, một giao thức ZKP phải thỏa mãn ba thuộc tính sau:
- Completeness (Đầy đủ): Nếu một đề xuất/ tuyên bố đúng, thì người chứng minh sẽ luôn có thể chứng minh cho người kiểm chứng rằng nó đúng và được chấp nhận, không bị bác bỏ.
- Soundness (Độ chính xác): Nếu một đề xuất/ tuyên bố sai, thì không ai có thể chứng minh cho người kiểm chứng rằng nó đúng và được chấp nhận. Điều này đảm bảo rằng hệ thống chỉ chấp nhận những yêu cầu/ tuyên bố đúng.
- Zero-knowledge (Không tiết lộ): Nếu một đề xuất/ tuyên bố đúng, thì không có người xác thực nào được biết bất kỳ thông tin nào về nhân chứng của tuyên bố. Tức là, thông tin liên quan đến nhân chứng của tuyên bố luôn được giữ bí mật và không được tiết lộ cho bất kỳ ai, bao gồm cả người xác thực.
1.2 ZERO-KNOWLEDGE PROOF ALGORITHMS
zk-SNARKs
zk-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge) là một loại hệ thống zero-knowledge proof cho phép người chứng minh thuyết phục người xác thực rằng họ có kiến thức về một bí mật mà không tiết lộ bí mật đó. Các zk-SNARKs được gọi là succinct (rút gọn) vì chúng có khả năng giảm kích thước của các bằng chứng xuống rất nhỏ, chỉ vài trăm byte. Điều này có nghĩa là chúng có khả năng xử lý các bằng chứng lớn trong thời gian rất ngắn, rút ngắn thời gian xác minh và giảm chi phí tính toán.
Cốt lõi của zk-SNARKs nằm trong các Chương trình Đại số Bậc Hai (Quadratic Arithmetic Programs - QAPs). Một QAP có thể đại diện cho bất kỳ mạch số học nào, bao gồm các cổng cộng và nhân. Dựa trên một QAP, người chứng minh (prover) có thể tạo ra một bằng chứng cho thấy họ biết các giá trị đầu vào mà không tiết lộ các giá trị đó. Quá trình xác minh cho zk-SNARKs có thể được biểu thị toán học như sau: Gọi C là một chu trình số học, và ϕ là một QAP đại diện cho C. Người chứng minh (prover) muốn chứng minh rằng họ biết các giá trị x1....xn sao cho C ( x1....xn ) = 0. Người chứng minh và người xác minh cùng sử dụng một chuỗi tham chiếu chung (CRS) σ:
- Prover tính toán một bằng chứng (proof) π = (πa,πb,πc) thuộc G^3 trong đó G là một nhóm đường cong elliptic
- Verifier kiểm tra xem phương trình sau có đúng không : πa * πb = πc * σ.
Ví dụ : Hãy giả định rằng chúng ta sử dụng zk-SNARKs để chứng minh rằng có thể tìm số nguyên tố trong dãy số từ 1 đến 100 mà không tiết lộ số nguyên tố cụ thể đó.
*Prover :
1. Tạo QAP:
Bắt đầu bằng cách tạo QAP để biểu diễn mạch số học mà bạn muốn chứng minh. Gọi x1, x2, ..., x100 là 100 biến đầu vào tương ứng với dãy số từ 1 đến 100. Giả sử bài toán là tìm số nguyên tố trong dãy số này, với f(x1, x2, ..., x100) thì hàm sẽ được tính toán như sau: Nếu x_i là số nguyên tố, thì f(x1, x2, ..., x100) sẽ bằng 0, còn nếu x_i không phải số nguyên tố thì nó sẽ bằng 1. Chúng ta có thể sử dụng QAP để biến đổi hàm này thành ba đa thức tuyến tính R(x), S(x) và T(x) sao cho R(x) * S(x) = T(x) và T(x) = 0 khi và chỉ khi f(x1, x2, ..., x100) = 0.
2. Tạo proof:
Sử dụng một công cụ tạo bằng chứng (prover) để tính toán các giá trị πa ,πb ,πc. Các giá trị này sẽ được tính toán trên đường cong elliptic và sử dụng CRS để tạo ra một proof. Nói cách khác, πa, πb, πc sẽ được tính toán dựa trên các giá trị đầu vào mà chúng ta cho vào kết hợp với chuỗi tham chiếu chung CRS. Khi tạo proof xong, sẽ gửi proof này cho người xác thực.
Verifier
3. Kiểm tra CRS
Đầu tiên, người xác thực sẽ kiểm tra tính hợp lệ của CRS bằng cách kiểm tra xem nó có thể được sử dụng để tạo ra proof hay không.
4. Xác minh tính đúng đắn của proof:
Nếu πa * πb và πc * (CRS) bằng nhau và khác 0, proof sẽ được xác minh là đúng đắn và được chấp nhận. Nếu không bằng nhau hoặc bằng 0, proof sẽ bị từ chối.
Link tham khảo về zk-SNARKs https://eprint.iacr.org/2013/879.pdf
zk-STARKs
zk-STARKs là một loại hệ thống chứng minh không tiết lộ tri thức (zero-knowledge proof system) mới được phát triển được dựa trên thuật toán Fast Fourier Transform (FFT). zk-STARKs cho phép người dùng chứng minh rằng họ biết một thông tin bí mật mà không cần tiết lộ thông tin đó cho người khác. Tuy nhiên, điểm khác biệt giữa zk-STARKs và các hệ thống zero-knowledge proof khác là zk-STARKs không yêu cầu thiết lập đáng tin cậy (trusted set-up) và là một hệ thống minh bạch, nghĩa là người dùng có thể kiểm tra kết quả chứng minh một cách dễ dàng.
Ý tưởng chính đằng sau zk-STARKs là sử dụng một giải pháp cam kết đa thức (polynomial commitment scheme) dựa trên cây Merkle. Để chứng minh việc biết một bí mật, người chứng minh cam kết với một đa thức và người xác minh kiểm tra xem đa thức đó có đáp ứng các thuộc tính nhất định không. Giao thức zk-STARKs có thể tóm tắt như sau:
- Người chứng minh sử dụng hệ thống cam kết đa thức (polynomial commitment scheme) để cam kết đến đa thức f(x) bằng cách tính toán các giá trị tại các điểm và xây dựng một cây Merkle với các giá trị đó làm lá.
- Người chứng minh sẽ gửi gốc Merkle và các giá trị trung gian đến người xác minh để tổ chức việc xác minh
- Người xác minh gửi các thử thách ngẫu nhiên đến người chứng minh. Người chứng minh tạo ra một chứng minh rằng đa thức f(x) đáp ứng các thử thách của người xác minh mà không tiết lộ đa thức hoặc các giá trị tại các điểm.
Để biết thêm thông tin về zk-STARK, hãy xem bài viết của 046.pdf (iacr.org)
Bulletproofs
Bulletproofs là một hệ thống bằng chứng không kiến thức, không tương tác được đề xuất lần đầu tiên vào tháng 12 năm 2017 bởi Nhóm mật mã ứng dụng của Stanford với sự đóng góp của Blockstream và Đại học College of London. Chúng là giải pháp thay thế hiệu quả và an toàn hơn cho các hệ thống ZKP trước đây, chẳng hạn như SNARK.
Đặc điểm quan trọng của Bulletproofs là kích thước chứng minh và thời gian xác minh logarithmic, làm cho chúng phù hợp cho việc sử dụng trong các ứng dụng blockchain nơi tính mở rộng rất quan trọng. Giao thức Bulletproofs bao gồm các bước sau:
- Người chứng minh cam kết đến một giá trị v bằng cách sử dụng cam kết Pedersen C = vG + rH, trong đó G và H là các bộ tạo nhóm đường cong elliptic, và r là một yếu tố che mờ ngẫu nhiên (random blinding factor).
- Người chứng minh tạo ra một chứng minh π để chứng minh rằng họ có kiến thức về v và r mà không tiết lộ chúng, và gửi chứng minh cho người xác minh.
- Người xác minh sẽ kiểm tra tính hợp lệ của chứng minh π bằng cách sử dụng cam kết C và các phát sinh G và H.
Một khía cạnh quan trọng của Bulletproofs là việc sử dụng lập luận tích vô hướng (inner product argument) để chứng minh các khẳng định về giá trị đã cam kết. Việc sử dụng lập luận tích vô hướng cho phép người chứng minh chứng minh rằng họ biết các vector a và b sao cho tích vô hướng ⟨a,b⟩=c mà không tiết lộ các vector đó.
Lập luận tích vô hướng có thể được viết như sau:
- Prover: Commit to a, b and ⟨a,b⟩=c
- Verifier: Check if ⟨a,b⟩=c
Ví dụ:
Hãy giả định rằng chúng ta sử dụng Bulletproofs để chứng minh rằng chúng ta biết một số nguyên tố trong khoảng từ 1 đến 100 mà không tiết lộ giá trị cụ thể của số đó.
Prover :
- Chọn ngẫu nhiên một số nguyên r trong khoảng từ 1 đến 100.
- Tính toán giá trị cam kết Pedersen C cho p bằng công thức sau : C = pG + rH
Trong đó :
- G và H là các bộ sinh của một nhóm đường cong elliptic.
- p là số nguyên tố mà người chứng minh muốn chứng minh rằng họ biết.
- r là giá trị số ngẫu nhiên được chọn ở bước 1.
-
Tạo chứng minh Bulletproof: Để chứng minh rằng p là số nguyên tố, người chứng minh sẽ sử dụng lập luận tích vô hướng. Một cách đơn giản để thực hiện điều này là tạo một số nguyên tố q bằng cách tính tích của tất cả các số nguyên tố trong khoảng từ 1 đến 100. Sau đó, người chứng minh tạo ra các vector a và b sao cho a chứa các phần tử của phân tích thừa số nguyên tố của p, và b chứa các phần tử của phân tích thừa số nguyên tố của q. Tiếp theo, người chứng minh tính toán tích vô hướng ⟨a, b⟩ để chứng minh rằng họ có kiến thức về phần tử a. Sau đó, người chứng minh tạo ra một chứng minh phạm vi (range proof) để chứng minh rằng giá trị của p thuộc vào khoảng từ 1 đến 100 mà không tiết lộ giá trị của p.
-
Gửi C, Bulletproof, và chứng minh phạm vi cho người xác minh.
Verifier:
- Xác minh tính đúng đắn của cam kết Pedersen, bằng cách tính toán lại giá trị của C và so sánh với giá trị gửi từ người chứng minh
- Xác minh rằng giá trị tích vô hướng ⟨a, b⟩ bằng cách tính toán lại giá trị và so sánh với giá trị gửi từ người chứng minh
- Xác minh rằng giá trị của p nằm trong khoảng từ 1 đến 100, bằng cách sử dụng chứng minh phạm vi.
- Nếu tất cả các bước đều được thực hiện đúng đắn thì người xác minh sẽ kết luận rằng người chứng minh có kiến thức về một số nguyên tố trong khoảng từ 1 đến 100 mà không tiết lộ giá trị cụ thể của số đó.
2. MOTIVATION AND CURRENT EFFORTS IN ZKML
Quay lại bài toán đầu bài, làm thế nào để Alice chứng minh với Bob là cô ấy có mô hình?
Nếu Alice có dữ liệu đầu vào và Bob có thông số của mô hình, chúng ta có thể sử dụng Zero-Knowledge Proofs để chứng minh (proof) rằng Alice đã train ra 1 model mà không cần tiết lộ dữ liệu thật của Alice. Các công thức toán học có thể được sử dụng để xác định các ràng buộc. Khi đó, Alice có thể sử dụng các giải thuật Zero-Knowledge Proofs để chứng minh rằng mình đã tìm thấy giải pháp hợp lệ thỏa mãn các ràng buộc mà không tiết lộ dữ liệu của mình.
Trong một thế giới mà nội dung do Trí tuệ nhân tạo tạo ra ngày càng giống với nội dung do con người tạo ra, sử dụng Zero-Knowledge có thể giúp chúng ta xác định rằng một nội dung cụ thể đã được tạo ra bằng cách áp dụng một mô hình cụ thể cho một đầu vào được chỉ định. Điều này có thể cung cấp một phương tiện để xác minh kết quả đầu ra từ các mô hình ngôn ngữ lớn như GPT4, các mô hình chuyển đổi văn bản thành hình ảnh như DALL-E 2 hoặc bất kỳ mô hình nào khác. Một ví dụ là áp dụng một mô hình học máy trên một số dữ liệu nhạy cảm, nơi người dùng sẽ biết kết quả của mô hình từ dữ liệu của họ mà không cần tiết lộ đầu vào của họ cho bất kỳ bên thứ ba nào (ví dụ như trong ngành y tế).
Tuy nhiên hiện tại phần cứng đáp ứng được nhu cầu tính toán tạo các chứng minh của các hệ thống ZK vẫn còn kém vài thứ bậc so với khả năng chứng minh một cái gì đó lớn như các mô hình ngôn ngữ lớn hiện có ("LLMs"), nhưng đã có một số tiến bộ trong việc tạo các chứng minh của các mô hình nhỏ hơn.
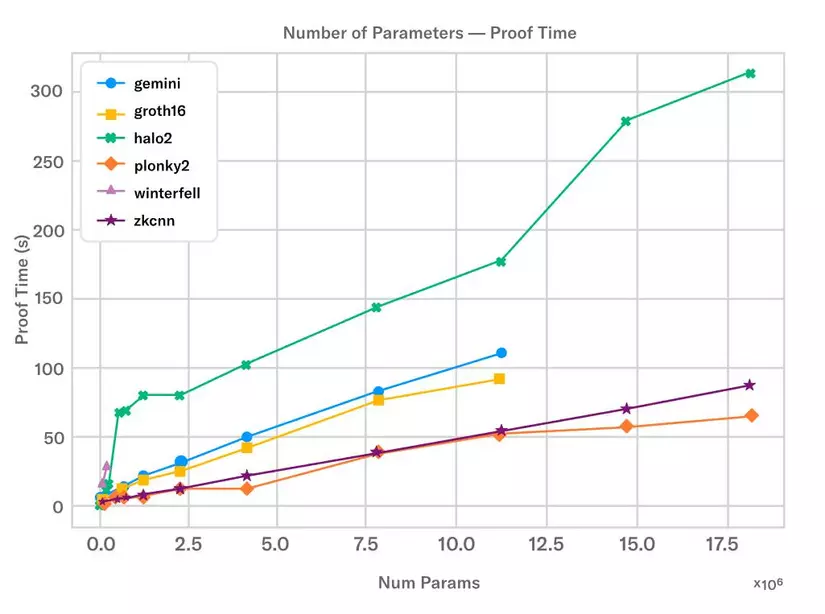
Hình 1: minh họa khả năng mở rộng của các hệ thống chứng minh khác nhau khi số lượng tham số của mạng neuron tăng lên.
Nguồn ảnh : https://worldcoin.org/blog/engineering/intro-to-zkml
Gần đây đội ngũ Modulus Labs vừa phát hành một bài báo mang tựa đề “The Cost of Intelligence”, trong đó họ đánh giá các ZK proof systems có đối sánh với một loạt các mô hình với kích thước khác nhau. Hiện nay, có thể tạo chứng minh(proof) cho các mô hình có khoảng 18 triệu tham số trong khoảng 50 giây chạy trên một máy AWS mạnh bằng hệ thống chứng minh như plonky2.
Nhiều nghiên cứu đang được thực hiện để tối ưu hóa phần cứng và cải thiện công nghệ ZK khiến tính toán các chứng minh ZK trở nên nhanh hơn và tiết kiệm tài nguyên hơn. Nếu công nghệ ZK tiếp tục được cải tiến, chúng ta sẽ có thể chứng minh các mô hình lớn hơn và trên các máy tính yếu hơn trong một thời gian ngắn hơn. Các tiến bộ này cũng mở ra cơ hội cho sự phát triển của các ứng dụng và trường hợp sử dụng mới của ZKML.
Tham khảo thêm tại : zkml-community/awesome-zkml: Aggregator for amazing ZKML resources (github.com)
3. Use case examples
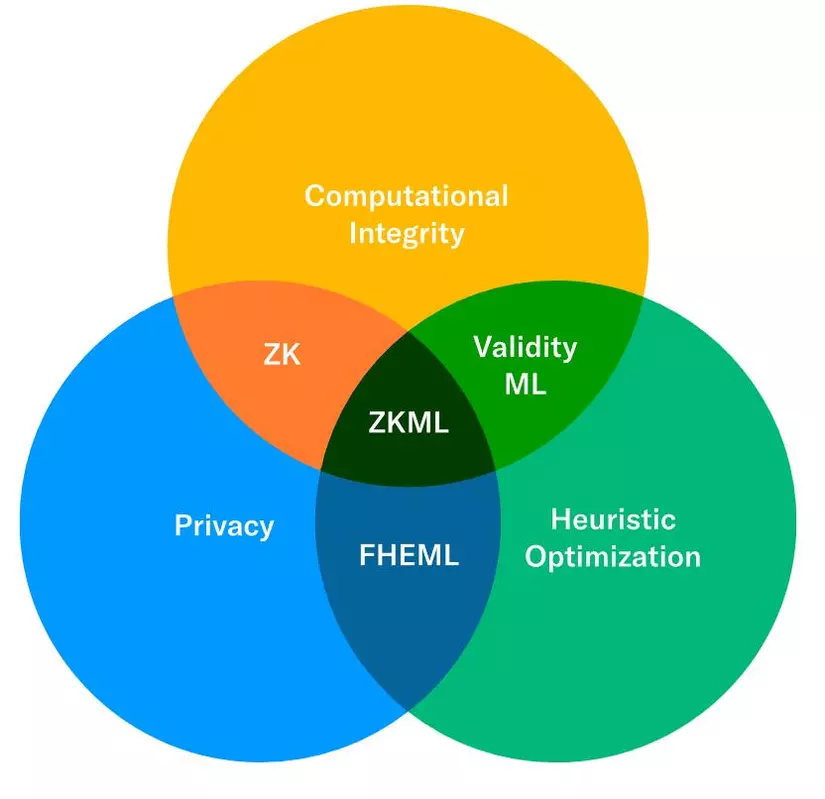Để quyết định liệu ZKML có thể được sử dụng cho một ứng dụng cụ thể, chúng ta có thể khảo sát cách thuộc tính của ZK sẽ hỗ trợ cho một số trường hợp sử dụng cụ thể. Ta có thể minh họa điều này dưới dạng Sơ đồ Venn.
Nguồn ảnh : https://worldcoin.org/blog/engineering/intro-to-zkml
COMPUTATIONAL INTEGRITY (VALIDITY ML)
Bằng chứng về tính hợp lệ (SNARK/STARK) có thể được sử dụng để chứng minh rằng một số tính toán đã diễn ra chính xác, trong ngữ cảnh của ML, đang chứng minh suy luận của mô hình ML hoặc một số mô hình đã tạo ra một số đầu ra bằng cách sử dụng một đầu vào cụ thể. ( ví dụ đầu bài ).
Khả năng dễ dàng chứng minh và xác minh rằng đầu ra là sản phẩm của một mô hình với đầu vào xác định. Điều này cho phép các mô hình ML chạy ngoài chuỗi trên phần cứng chuyên dụng có bằng chứng ZK của chúng, có thể dễ dàng xác minh trên chuỗi.
Ví dụ:
Giza đang giúp Yearn (một giao thức tổng hợp lợi nhuận DeFi) chứng minh rằng một số chiến lược lợi nhuận phức tạp sử dụng ML đang được thực thi chính xác trên chuỗi.
TÍNH MINH BẠCH CỦA ML DƯỚI DẠNG DỊCH VỤ (MLAAS)
Khi các công ty khác nhau cung cấp quyền truy cập vào các mô hình ML thông qua API của họ, với tư cách là người dùng, thật khó để biết liệu nhà cung cấp dịch vụ có thực sự cung cấp mô hình mà họ nói hay không vì API là một hộp đen. Việc cung cấp bằng chứng hợp lệ được đính kèm với API của các mô hình ML sẽ hữu ích để mang lại sự minh bạch cho người dùng vì họ có thể xác minh mô hình nào họ đang sử dụng.
ZK ANOMALY/FRAUD DETECTION
Cho phép tạo bằng chứng ZK về khả năng khai thác/gian lận. Các mô hình phát hiện bất thường có thể được đào tạo trên dữ liệu hợp đồng thông minh và được các DAO đồng ý là số liệu thú vị để có thể tự động hóa các quy trình bảo mật như tạm dừng hợp đồng theo cách phòng ngừa, chủ động hơn. Có những công ty mới thành lập đã xem xét việc sử dụng các mô hình ML cho mục đích bảo mật trong bối cảnh hợp đồng thông minh, vì vậy, bằng chứng phát hiện sự bất thường của ZK có thể là bước tiếp theo.
PRIVACY (ZKML)
Bên cạnh các bằng chứng hợp lệ, ZK cũng có thể ẩn các phần tính toán để kích hoạt ứng dụng bảo vệ quyền riêng tư của ML. Một vài ví dụ có thể được tìm thấy dưới đây:
- Decentralized Kaggle: bằng chứng rằng một mô hình có độ chính xác cao hơn x% trên một số dữ liệu thử nghiệm mà không tiết lộ trọng số.
- Privacy-preserving inference: Điều này liên quan đến việc bảo vệ quyền riêng tư trong việc sử dụng dữ liệu bệnh nhân cho các chẩn đoán y tế. Thay vì chia sẻ toàn bộ dữ liệu bệnh nhân cho các mô hình học máy, các bệnh nhân có thể chia sẻ dữ liệu của họ vào mô hình nhưng mà chỉ được chia sẻ kết quả chẩn đoán đối với bệnh nhân đó. Ví dụ: nếu một bệnh nhân sử dụng mô hình để kiểm tra xem mình có ung thư không, kết quả của kiểm tra sẽ được gửi trực tiếp đến bệnh nhân đó để giữ cho thông tin của họ được bảo mật.
Tham khảo thêm bài viết về Verifiable Convolutional Neural Network based on zk-SNARKs : 584.pdf (iacr.org)
Mình tin rằng trong tương lai khi mà các yếu tố phần cứng được giải quyết thì ZKML sẽ thay đổi rất lớn trong cách giải quyết của các bài toán trong bối cảnh bùng nổ và phát triển của các LLMs như hiện nay. Xu hướng trong tương lai là các Trustworthy AI sẽ được hình thành và rõ ràng hơn.
Cảm ơn mọi người đã đọc, nếu có sai sót hoặc thắc mắc gì trong bài viết, mọi người comment phía dưới nhé !!!
REFERENCES
[1] https://a16zcrypto.com/.../checks-and-balances-machine.../