Được công bố tại ICLR 2020 trong bài báo On the Variance of the Adaptive Learning Rate and Beyond của tác giả Liu và các cộng sự, Rectified Adam (Adam được chỉnh sửa), hay RAdam, là một biến thể của trình tối ưu hóa ngẫu nhiên Adam đưa ra một ý tưởng để điều chỉnh phương sai của learning rate thích ứng. Bài viết này giới thiệu về Adam cũng như Rectified Adam để ta có thể cùng hình dung được ở mức độ nào đó cách mà RAdam được kì vọng sẽ cải thiện hơn so với phiên bản trước đó.

Về Adam

Hẳn là dù đã từng tìm hiểu về Deep Learning thì chúng ta đề được học về Hồi quy logistic, bài toán thường được sử dụng để minh họa cho mô hình neural network đơn giản nhất chỉ với input layer và output layer.

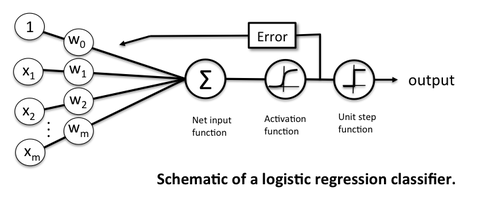
Thông thường, chúng ta thường được dạy rằng $f(w, x) = w_1^Tx + w_0$ sao đó sử dụng các hàm softmax mà một trong số đó là hàm logictics $\sigma(z) = \frac{1}{1+e^{{-z}}}$ với giá trị $z = f(w, x)$ để thu được đầu ra dưới dạng xác suất để phục vụ cho việc tính toán lỗi bằng hàm $\mathcal{L}_D = \frac{1}{|D|} \sum_{(x, y) \in D} L \left( f_{w, x}, y \right)$ . Bằng cách tối ưu hàm lỗi bằng một số phương pháp mà thường được sử dụng bằng Gradient Descent, chúng ta kì vọng sẽ thu được bộ trọng số w (bao gồm $w_1$ và $w_0$ ) tối ưu. Quá trình này được gọi là quá trình học mà trong đó, $w$ được cập nhật theo công thức như sau:

$w^{(k+1)}=w^{(k)}-\eta\nabla_\theta L(w^{(k)})$

Với $\eta$ là giá trị learning rate được chọn từ trước và thường có giá trị rất nhỏ.

Các thuật toán tối ưu

Mặc dù được kỳ vọng rằng sẽ hội tụ tại điểm cực tiểu toàn cục của hàm lỗi sau số lượt huấn luyện hữu hạn, tuy nhiên vẫn có trường hợp quá trình học bị "kẹt" lại ở điểm cực tiểu địa phương, vậy nên các phương pháp sử dụng ý tưởng động lượng (momentum) để giúp quá trình học dễ dàng tiến đến điểm tối ưu.

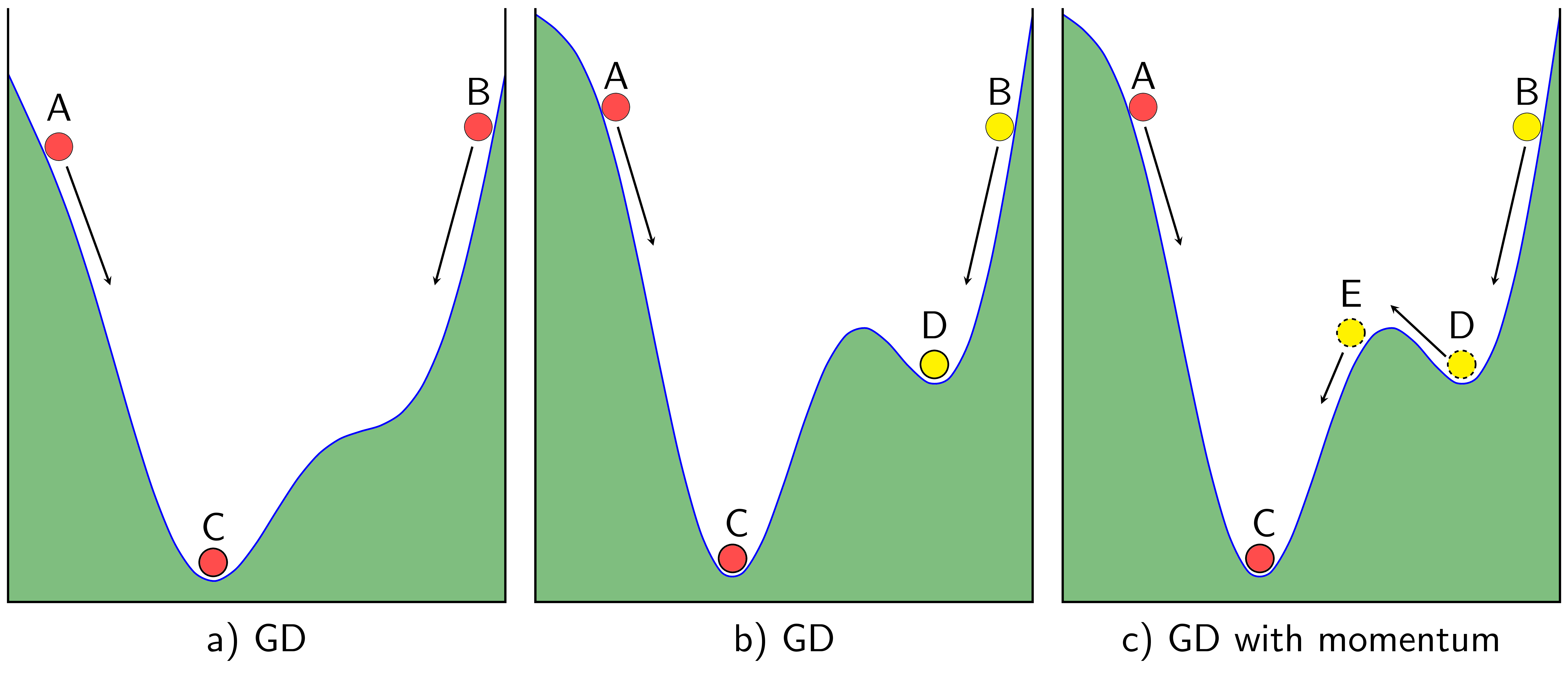
Hình ảnh từ https://machinelearningcoban.com/2017/01/16/gradientdescent2/

Momentum hay động năng xuất phát khái niệm động nằng trong vật lý với ý tưởng rằng nếu cung cấp động năng cho vật đang di chuyển liên tục theo cùng một hướng. Bởi vậy, Momentum có công thức cập nhật $w$ theo đại lượng $v^{(k+1)}= \gamma v^{(k)} + \eta \nabla_{w}J(w^{(k)})$ là lượng thay đổi ở thời điểm $k$ như sau:

$w^{(k+1)}=w^{(k)} - v^{(k+1)}$

Tiếp theo đó, learning rate, như giới thiệu trên, tuy có tác động không nhỏ đến quá trình huấn luyện nhưng lại chỉ được lựa chọn theo kinh nghiệm và được đặt cố định trong suốt quá trình huấn luyện. Bởi vậy một số thuật toán như Adadelta và RMSProp được đề xuất. Các thuật toán này coi learning rate không còn là hằng số như trước kia và được điều chỉnh qua mỗi lần học được thể hiện thông qua các công thức cập nhật dưới đây:

Với Adadelta, thuật toán này sử dụng biến $s_t$ để tích luỹ phương sai của các gradient trong quá khứ như sau:

$g_t = \nabla_\theta L(w)$

$s_t = \mathbf{s}_{t-1} + \mathbf{g}_t^2$

$w_t = \mathbf{w}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \cdot \mathbf{g}_t$

Trong khi đó RMSProp giảm dần sự phụ thuộc vào các gradient trong quá khứ bằng cách sử dụng giá trị $\gamma$ có giá trị trong khoảng $(0, 1)$

$s_t \leftarrow \gamma \mathbf{s}_{t-1} + (1 - \gamma) \mathbf{g}_t^2$

$x_t \leftarrow \mathbf{x}_{t-1} - \frac{\eta}{\sqrt{\mathbf{s}_t + \epsilon}} \odot \mathbf{g}_t$

Và cuối cùng là Adam, thuật toán thường được xem là sự kết hợp của Momentum và RMSprop. Công thức cập nhật của Adam được trình bày như sau:

$g_t = \nabla_\theta L(w_{t-1})$

$m_t = \beta_1 . m _{t-1} + (1 - \beta_1) . g_t$

$v_t = \beta_1 . m _{t-1} + (1 - \beta_1) . g_t^2$

$\widehat{m}_t = m_t/(1 -\beta^t_1)$

$\widehat{v}_t = v_t/(1 -\beta^t_2)$

$w_t = w_{t-1} - \frac{\alpha . \widehat{m}}{\sqrt{v_t + \epsilon}} \cdot g_t$

Với $\alpha$ là Stepsize được xác định trước. Quan sát công thức trên, ta có thể thấy rằng Adam sử dụng cả ý tưởng về động lượng và tích lũy phương sai của gradient của hai thuật toán trên. Mặc dù còn có một số vấn đề đặc biệt là có một số trường hợp Adam có thể phân kỳ do việc kiểm soát phương sai kém (On the convergence of adam and beyond ) Adam vẫn là một trong các thuật toán được sử dụng nhiều nhất trong thời điểm hiện nay.

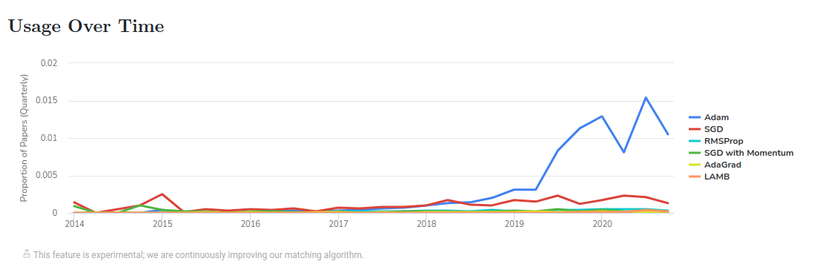
Hình ảnh từ https://paperswithcode.com/method/adam

Rectified Adam

Vấn đề được đề cập trong paper On the Variance of the Adaptive Learning Rate and Beyond cũng như On the convergence of adam and beyond chỉ ra rằng Adam có thể phân kỳ do việc kiểm soát phương sai kém. Cụ thể vấn đề này được được trình bày khá tường minh trong hai paper trên, phần sau chỉ tóm tắt lại theo ý hiểu của mình

Theo bài báo của Reddi và các cộng sự công bố năm 2018, các thuật toán tối ưu stochastic gradient descent, gọi là generic adaptive methods được mô tả bởi một generic framework như hình dưới đây:

Cụ thể, các thuật toán tối ưu hóa khác nhau có thể được chỉ định bằng các lựa chọn khác nhau của $φ(.)$ Và $ψ(.)$ , Trong đó $φ(.)$ là hàm tính động lượng tại bước thời gian t và $ψ(.)$ là adaptive learning rate tại thời điểm t được tính toán. Để tiện theo dõi cũng như đọc lại trong paper, chúng ta sẽ cố gắng sử dụng thống nhất các ký hiệu này. Phần tiếp theo trong paper, nhóm tác giả bắt đầu trình bày về thử nghiệm của mình như sau:

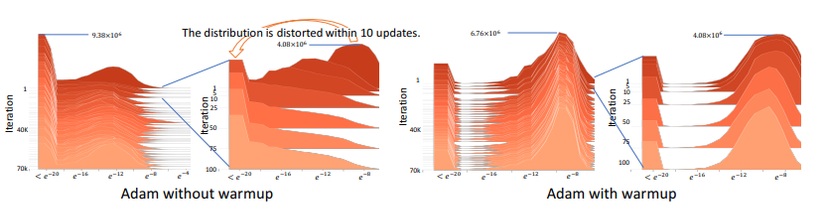
Hình ảnh trên được trích từ papper trực quan hóa histogram của giá trị tuyệt đối của gradient trên thang log được nhóm tác giả cung cấp để minh họa cho quá trình thí nghiệm của mình. Phương pháp warmup dùng trong thi nghiệm trên xuất phát ý tưởng sẽ sử dụng một giá trị nhỏ hơn trong những lần lặp đầu. Được sử dụng như một ví dụ, một warmup $α_t = tα_0$ với $t < T_w$ được sử dụng và kết quả thu được, được thể hiện trong hình trên, cho thấy phân bố gradient bị "bóp méo". Sự biến dạng gradient như vậy có nghĩa là Adam gốc bị mắc kẹt trong điểm tối ưu xấu sau một vài bản cập nhật đầu tiên. Warmup về cơ bản làm giảm tác động của các lần cập nhật có vấn đề này để tránh sự cố hội tụ. Từ đó, nhóm tác giả đưa gia nhận định của mình rằng:

Do thiếu mẫu trong giai đoạn đầu, adaptive learning rate có một phương sai lớn không mong muốn, dẫn đến optima cục bộ xấu và làm ảnh hướng không tốt đến quá trình học. (Nguyên văn: Due to the lack of samples in the early stage, the adaptive learning rate has an undesirably large variance, which leads to suspicious/bad local optima.)

Vấn đề phương sai và cơ sở của Rectified Adam

Để chứng minh nhận định của mình, nhóm tác giả paper On the Variance of the Adaptive Learning Rate and Beyond đã giải thích bằng cách làm rõ tại sao Adam kiểm soát phương sai kém cũng như phương pháp họ đề xuất cải thiện vấn đề trên như thế nào. Nội dung phần đó sẽ được trình bày tóm tắt ở phần dưới đây.

Phương sai của adaptive learning rate

Nhóm tác giả bắt đầu trình bày bằng cách xét một trường hợp đặc biệt rằng với $t=1$ chúng ta có $\psi(g_1) = \sqrt{{1}/{g_1^2}}$ coi $\left\{g_1 \ldots g_t\right\}$ là mẫu ngẫu nhiên tuân theo phân bố $\mathcal{N}(0, \sigma^2)$ . Do đó, $1/{g_t^2}$ tuân theo một scale-inverse-chi-square distribution (phân phối chi bình phương nghịch đảo mở rộng) $ScaledInvChiSquare(1, 1/{\sigma^2})$ và phương sai $var[\sqrt{{1}/{g_1^2}}]$ là phân kỳ. Nó có nghĩa là tỷ lệ thích nghi có thể lớn không thể lường trước được trong giai đoạn học đầu tiên. Trong khi đó, đặt một learning rate nhỏ ở giai đoạn đầu có thể làm giảm phương sai do $var[αx]=α^2 var[x]$ do đó làm giảm bớt vấn đề này. Do đó, họ cho rằng chính sự chênh lệch không giới hạn của adaptive learning rate trong giai đoạn đầu là nguyên nhân dẫn đến các lần cập nhật này có vấn đề.

Sử dụng warmup để giảm phương sai

Để kiểm tra rõ hơn, nhóm tác giả thiết kế một tập hợp các thử nghiệm được kiểm soát để xác minh giả thuyết của mình. Đặc biệt, họ thiết kế hai biến thể của Adam làm giảm phương sai của tỷ lệ học thích ứng: Adam-2k và Adam-eps và so sánh kết quả với phiên bản Adam gốc.

Về cơ bản, Adam-2k, theo đúng tên gọi của nó, sử dụng mốc lần cập nhật thứ 2000 để giảm phương sai bằng cách chỉ cập nhật $\psi(.)$ giữ nguyên $φ(.)$ và tham số $\theta$ trong 2000 lần cập nhật và từ lần cập nhật thứ 2001 trở đi sẽ cập nhật theo quy tắc của Adam bản gốc. Kết quả thực nghiệm cho thấy rằng, sau khi lấy thêm hai nghìn mẫu này để ước tính tốc độ học tập thích ứng, Adam-2k tránh được vấn đề hội tụ của Adam bản gốc. Ngoài ra, so sánh kết quả được thể hiện trong các biểu đồ dưới đây, ta có thể thấy rằng việc lấy mẫu đủ lớn sẽ ngăn không cho phân bố gradient bị bóp méo. Những quan sát này xác minh giả thuyết của nhóm tác giả rằng việc thiếu đủ mẫu dữ liệu trong giai đoạn đầu là nguyên nhân gốc rễ của vấn đề hội tụ.

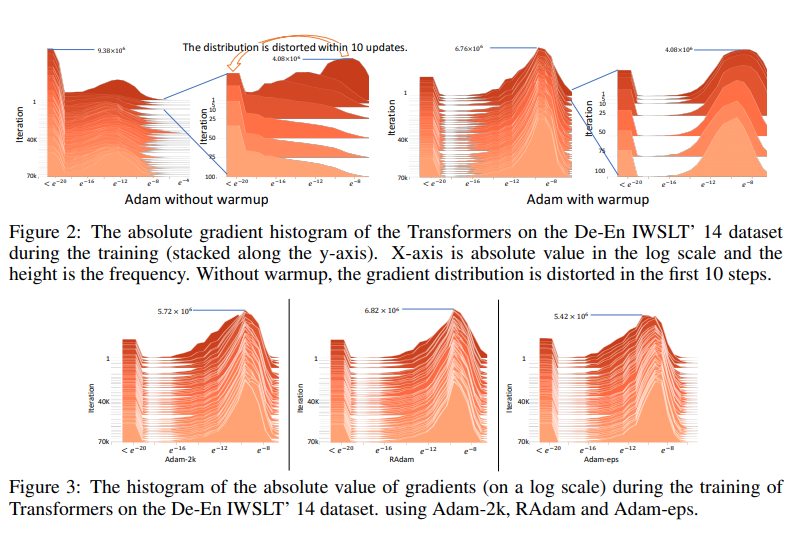
Một cách đơn giản khác để giảm phương sai là tăng giá trị của $\epsilon$ trong công thức ${\hat\psi(g_1, ..., g_t)} = \frac{\sqrt{1-\beta^t_2}}{\epsilon + \sqrt{(1-\beta_2) \sum_{i=1}^t{\beta_2^{t-1}g^2_i}}}$ . Trên thực tế, nếu chúng ta giả sử ${\hat\psi(.)}$ tuân theo phân phối đồng đều, phương sai của nó bằng $\frac{1}{12\epsilon^2}$ ?? ?? Do đó, nhóm tác giả đề xuất thêm Adam-eps sử dụng giá trị $\epsilon$ lớn chẳng hạn như $10^{-4}$ thay cho giá trị $10^{-8}$ của phiên bản gốc. Ta có thể quan sát thấy rằng nó không bị vấn đề hội tụ nghiêm trọng của phiên bản Adam gốc và điều này chứng tỏ rằng chứng tỏ thêm rằng vấn đề hội tụ có thể được giảm bớt bằng cách giảm phương sai của tốc độ học thích ứng và cũng giải thích tại sao việc điều chỉnh lại quan trọng trong thực tế và cũng như Adam-2k, nó ngăn không cho phân bố gradient bị bóp méo. Tuy nhiên, khi so sánh với Adam có warmup cũng như Adam-2k, nhóm tác giả thấy rằng Adam-eps có hiệu năng kém hơn hai phương pháp trên. Do đó, họ cho rằng cần có cách phương pháp chặt chẽ hơn và tổng quát hơn để xác định để kiểm soát phương sai của adaptive learning rate.

Kiểm soát phương sai bằng cách có học hơn

Như đã đề cập ở các nghiên cứu trước đây, Adam sử dụng exponential moving average để tính adaptive learning rate. Đối với các gradient $\left\{g_1 \ldots g_t\right\}$ , exponential moving average của chúng có phương sai lớn hơn simple average của chúng. Cùng với đó, trong các stage đầu với t nhỏ, lượng thay đổi của exponential weights của $\left\{g_1 \ldots g_t\right\}$ là tương đối nhỏ. Bởi vậy nhóm tác giả giả định $\frac{\sqrt{1-\beta^t_2}}{\epsilon + \sqrt{(1-\beta_2) \sum_{i=1}^t{\beta_2^{t-1}g^2_i}}}$ cũng tuân theo phân phối chi bình phương nghịch đảo tỷ lệ với $ρ$ bậc tự do. Dựa trên giả thiết này,ta có thể tính được $Var[ \psi^2 (.)]$ và hàm mật độ xác suất của $\psi^2(.)$

Bằng một số phép màu, cụ thể là phân tích phương sai căn bậc 2 của $Var[ \psi^2 (.)]$ , tức là $Var[ \psi (.)]$ , nhóm tác giả thu được rằng nếu $\psi^2 (.)$ tuân theo môt scale-inverse-chi-square distribution $ScaledInvChiSquare(1, \frac{1}{\sigma^2})$ , $Var[ \psi (.)]$ đơn điệu giảm khi $\rho$ tăng. Cụ thể với $\rho > 4$ ta có:

$Var[ \psi^2 (.)] = \mathcal{E}[ \psi^2 (.)] - {\mathcal{E}[ \psi (.)]}^2 = \tau^2(\frac{\rho}{\rho -2}- \frac{\rho2^{2\rho-5}}{\pi}\Beta(\frac{\rho - 1}{2}, \frac{\rho - 1}{2})^2)$

Nó cho thấy rằng, do thiếu các mẫu huấn luyện được sử dụng trong giai đoạn đầu, Var [ψ (.)] lớn hơn nhiều so với các giai đoạn sau. Để kiểm soát phương sai, nhóm tác giả thực hiện phân tích lượng hóa trên Var [ψ (.)] bằng cách ước tính số bậc tự do ρ.

Ước lượng $\rho$ và phương sai

Nếu đã đọc đến đây thì xin chúc mừng, các bạn sẽ đọc một tỉ thứ toán nữa. Như đề cập trên, trước tiên, nhóm tác giả đưa ra ước lượng ρ dựa trên $t$ để tiến hành phân tích định lượng cho $Var [\psi(g_1, · · ·, g_t)]$ , sau đó chúng tôi mô tả thiết kế cách thức ước lượng learning rate và so sánh nó với các phương pháp heuristic (phần heuristic các bạn tự đọc nhé )

Bằng một cách kì diệu nào đó được đề cập trong Forecasting with moving averages exponential moving average (EMA) có thể được hiểu là sự xấp xỉ với simple moving average (SMA) trong ứng dụng thực tế

$p(\frac{(1-\beta_2)\sum_i=1^t\beta_2^{t-i}g_i^2}{1- \beta^t_2}) \approx p(\frac{\sum^{f(t, \beta_2)}_{i=1}g^2_{t+1-i}}{f(t, \beta_2)})$

Với $f(t, \beta_2)$ là độ dài của SMA để SMA có chung trọng tâm với EMA, đọc thêm tại Relationship between SMA and EMA. Nói cách khác $f(t, \beta_2)$ cần thỏa mãn điều kiện:

$(1- \beta_2)\sum^{t}_{i=1}\beta^{i-1}_2(t+1-i)/(1-\beta^t_2) = \sum^{f(t, \beta_2)}_{i=1}(t+1 - i)/f(t, \beta_2)$

Bằng cách giải phương trình trên, nhóm tác giả có được $f(t, \beta_2) = \frac{2}{1-\beta_2} - 1 -\frac{2t\beta^t_2}{1-\beta^t_2}$ . Cùng với việc coi $\psi^2 (.)$ tuân theo phân bố $ScaledInvChiSquare(1, \frac{1}{\sigma^2})$ và coi $g_i$ là mẫu ngẫu nhiên tuân theo phân bố $\mathcal{N}(0, \sigma^2)$ ta có $\frac{\sum^{f(t, \beta_2)}_{i=1}g^2_{t+1-i}}{f(t, \beta_2)}$ tuân theo phân bố $ScaledInvChiSquare(f(t, \beta_2), \frac{1}{\sigma^2})$ . Do ta đã coi $ScaledInvChiSquare(f(t, \beta_2), \frac{1}{\sigma^2})$ như một xấp xỉ của $ScaledInvChiSquare(\rho, \frac{1}{\sigma^2})$ nên tac có thể coi $f(t, \beta_2)$ như một ước lượng của $\rho$ . Từ đây, nhóm tác giả kí hiệu $f(t, \beta_2)$ là $\rho_t$ và $\frac{2}{1- \beta_2} - 1$ là $\rho_\infty$ do $f(t, \beta_2) \leqslant lim_{t \rightarrow \infty}f(t, \beta_2) = \frac{2}{1- \beta_2} - 1$

Tiếp đó dựa trên ước lượng ở phần trên, ta có $Var[ \psi^2 (.)] = \mathcal{E}[ \psi^2 (.)] - {\mathcal{E}[ \psi (.)]}^2 = \tau^2(\frac{\rho}{\rho -2}- \frac{\rho2^{2\rho-5}}{\pi}\Beta(\frac{\rho - 1}{2}, \frac{\rho - 1}{2})^2)$ và cùng với đó giá trị này đơn điệu giảm khi $\rho$ tăng và đạt cực tiểu tại $\rho_t=\rho_\infty$ .

Mặc dù chúng ta có dạng giải tích của Var [ψ (.)] như ở tít phía trên, nó không ổn định về mặt số học. Vì vậy, nhóm tác giả sử dụng xấp xỉ bậc nhất để tính toán hạn chỉnh lưu. Cụ thể, bằng cách tính gần đúng $\sqrt{\psi^2(.)}$ với bậc đầu tiên dựa trên Taylor series methods

$\sqrt{\psi^2(.)} \approx \sqrt{\mathcal{E}[\psi^2(.)]} + \frac{1}{2\sqrt{\mathcal{E}[\psi^2(.)]}}(\psi^2(.) - \mathcal{E}[\psi^2(.)])$

và

$Var[\psi(.)] \approx \frac{Var[\psi^2(.)] }{\mathcal{E}[\rho^2(.)]}$

Do coi $\psi^2 (.)$ tuân theo một $ScaledInvChiSquare(\psi_t, \frac{1}{\sigma^2})$ nên ta có:

$Var[\psi(.)] \approx \rho_t/[2(\rho_t-2)(\rho_t-4)\sigma^2]$

Dựa trên công thức trên, chúng ta biết $Var[\sqrt{(\psi(.))}]$ giảm với tốc độ xấp xỉ $\mathcal{O}(\frac{1}{\rho_t})$ . Từ xấp xỉ này, nhóm tác giả tính toán giá trị cho $\tau$ , được gọi là rectification term hay hạn chỉnh lưu, như sau:

$\tau_t = \sqrt{\frac{(\rho_t-4)(\rho_t -2)\rho_\infty}{(\rho_\infty-4)(\rho_\infty -2)\rho_t}}$

Áp dụng $\tau_t$ vào Adam, nhóm tác giả đưa ra một biến thể mới của Adam, Adam được chỉnh sửa (Rectified Adam, Adam), như được tóm tắt như sau:

Cụ thể, khi độ dài của SMA xấp xỉ nhỏ hơn hoặc bằng 4, phương sai của adaptive learning rate là khó vàadaptive learning rate không được sử dụng. Nếu không, thuật toán sẽ tính toán tính toán $\tau_t$ và cập nhật các thông số vớiadaptive learning rateg. Điều đáng nói là, nếu $\beta_2 \leqslant 0.6$ , chúng ta có $\rho_\infty \leqslant 4$ , và RAdam bị suy biến thành SGD sử dụng động lượng.

Thực nghiệm

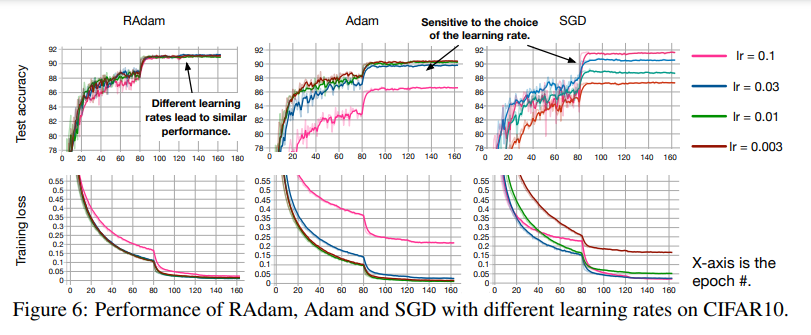
Để kiểm tra hiệu năng của phương pháp mới này, nhóm tác giả đánh giá RAdam bằng cách sử dụng một số bộ dữ liệu như: One Billion Word cho language modeling; Cifar10 và ImageNet cho image classification; IWSLT’14 De-En/EN-DE and WMT’16 EN-De cho neural machine translation nhằm so sánh kết quả thu được khi sử dụng RAdam so với việc dùng Adam phiên bản gốc cũng như Adam có dùng warmup. Kết quả được thể hiện ở biểu đồ dưới đây cho thấy rằng các tỉ lệ learning rate khác nhau đều mang tới hiệu năng tương đương nhau bởi vậy việc lựa chọn learning rate khác nhau sẽ không ảnh hưởng quá nhiều đến quá trình huấn luyện như trước.

Mã cài đặt của Rectified Adam

Mã cài đặt cho Pytorch của RAdam được nhóm tác giả công bố tại https://github.com/LiyuanLucasLiu/RAdam. Không chỉ vậy repo này còn chứa mã nguồn của các thử nhiệm của nhóm tác giả trển các bộ dữ liệu trên để ta có thể tiện tham khảo.

Phần mã cài đặt của RAdam không quá phức tạp để có thể đọc. So sánh với class RAdam_4step và AdamW được cung cấp cùng với RAdam, ta có thể thấy rằng trong hàm step, RAdam kiểm tra điều kiện state['step'] lớn hơn 4 và sau đó tính toán các giá trị dựa trên các công thức đã được cung cấp ở trên.

Tổng kết

Bài viết này trình bày lại bài báo về RAdam và các kiến thức liên quan dựa trên cơ sở tự tìm hiểu thêm về thuật toán tối ưu state-of-the-art này. Có thể thấy rằng không chỉ các kiến trúc mạng mới mà các thuật toán tối ưu như Adam và RAdam, ... cũng nhận được rất nhiều sự quan tâm để tìm hiểu cũng như cải tiến. Việc làm quen cũng như hiểu được đại ý về ý tưởng của những thứ này giúp chúng ta có thể dễ dàng sử dụng hơn trong tương lai. Bài viết đến đây là kết thúc cảm ơn mọi người đã giành thời gian đọc.

Rectified Adam thì khác gì Adam

Về Adam

Các thuật toán tối ưu

Rectified Adam