SVM
SVM (Support Vector Machine) là một thuật toán học máy được sử dụng trong bài toán phân loại và hồi quy, được sử dụng nhiều nhất trong học máy trước khi mạng nơ ron nhân tạo trở lại với các mô hình deep learning. SVM chỉ có thể hoạt động trên dữ liệu tuyến tính. Mục tiêu của thuật toán này là tìm cách xác định một siêu phẳng trong không gian N chiều (ứng với N đặc trưng) để phân chia các điểm dữ liệu thành các lớp . Mục tiêu của SVM là tìm một siêu phẳng có khoảng cách lớn nhất với các điểm dữ liệu gần nhất của các lớp tương ứng với lớp của chúng. (Nghĩa là mục tiêu của chúng ta là tìm siêu phẳng có lề hay khoảng cách tới các điểm của 2 lớp là lớn nhất).
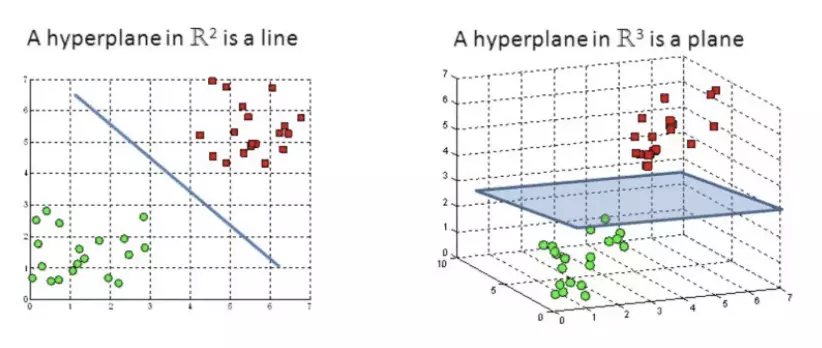
Trong không gian N chiều, một siêu phẳng sẽ có kích thước là N-1 chiều. Siêu phẳng tạo ra một biên giới để phân chia 2 lớp của dữ liệu.(hình SVM(2)). Chú ý rằng số chiều của siêu phẳng sẽ phụ thuộc vào số đặc trưng (feature), và các điểm dữ liệu nằm trên hoặc gần nhất với siêu phẳng được gọi là vecto hỗ trợ, chúng ảnh hưởng đến vị trí và hướng của siêu phẳng.
Soft Margin SVM
Soft Margin SVM là một biến thể của SVM, sử dụng trong trường hợp dữ liệu được phân tách tuyến tính, khi chúng ta không thể vẽ được đường thẳng để phân loại các điểm dữ liệu. Thuật toán này cho phép SVM mắc một số lỗi nhất định với mục tiêu giữ cho lề càng rộng càng tốt và các điểm khác vẫn được phân loại chính xác. Nói cách khác, nó sẽ cân bằng giữa việc phân loại sai và tối đa hóa lề. Sự cho phép vi phạm một số điểm dữ liệu giúp giảm thiểu overfitting (quá khớp) và làm cho mô hình SVM linh hoạt hơn trong việc xử lý các tập dữ liệu có độ phức tạp cao hơn.
Một đại lượng quan trọng và để kiểm soát mức độ sai sót của Soft Margin SVM là mức độ chấp nhận lỗi (hay tham số phạt). Khi tham số phạt càng lớn nghĩa là SVM bị phạt càng nặng khi phân loại sai và kết quả sẽ cho ra 1 lề ( margin) hẹp và ngược lại.
Kernel SVM
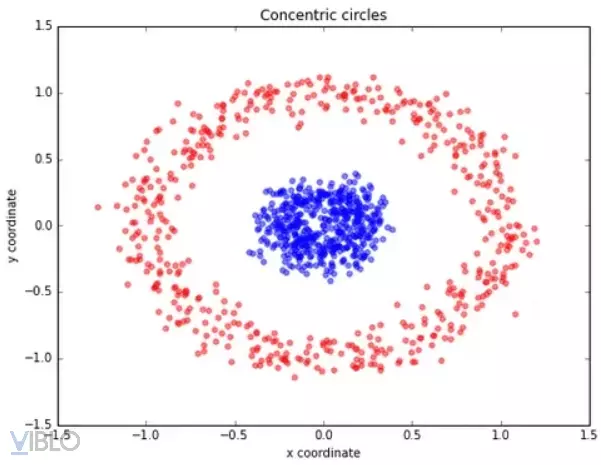
Kernel SVM (Support Vector Machine) là một phiên bản mở rộng của SVM cho phép xử lý các tập dữ liệu không tuyến tính bằng cách sử dụng hàm nhân (kernel function). Thay vì tìm một siêu phẳng trong không gian ban đầu, Kernel SVM ánh xạ dữ liệu vào không gian nhiều chiều hơn thông qua hàm nhân và sau đó tìm một siêu phẳng phân chia tuyến tính trong không gian mới. Các hàm nhân phổ biến được sử dụng bao gồm hàm đa thức (polynomial kernel), hàm Radial Basis Function (RBF kernel), và hàm sigmoid. Hình dưới đây sẽ minh họa về sự tiện lợi trong việc tìm kiếm siêu phẳng (hyperplane) khi chuyển đổi dữ liệu từ 2 chiều (dimension) sang 3 chiều (dimension) sử dụng Polynomial kernel. ( Hình Kernel trick)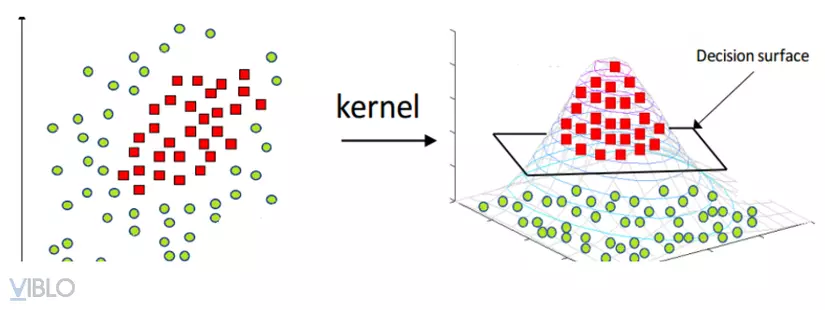
Multi-class SVM
Multi-class SVM là một dạng SVM được sử dụng cho bài toán phân loại đa lớp (multi-class classification). SVM gốc chỉ xử lý được bài toán phân loại nhị phân (binary classification). Để xử lý các tập dữ liệu có nhiều hơn hai lớp, Multi-class SVM sử dụng các phương pháp như One-vs-All (OvA) hoặc One-vs-One (OvO). Trong phương pháp OvA, mỗi lớp được so sánh với tất cả các lớp khác để tạo ra một bài toán phân loại nhị phân riêng biệt. Trong phương pháp OvO, một bài toán phân loại nhị phân được tạo ra cho mỗi cặp lớp khác nhau. Sau đó, kết quả của các bài toán nhị phân được kết hợp để đưa ra dự đoán cuối cùng cho bài toán phân loại đa lớp.
Ví dụ, nếu chúng ta có 3 lớp (A, B, C) trong bài toán phân loại đa lớp, phương pháp OvA sẽ tạo ra 3 bài toán nhị phân riêng biệt: A vs. (B, C), B vs. (A, C), C vs. (A, B). Mỗi bài toán nhị phân sẽ xác định xem một điểm dữ liệu thuộc lớp nào. Kết quả của các bài toán nhị phân sau đó được kết hợp để xác định lớp cuối cùng cho một điểm dữ liệu.
Phương pháp OvO sẽ tạo ra một số lượng bài toán nhị phân bằng số lớp nhân với số lớp trừ đi 1, tức là ở ví dụ trên sẽ tạo ra 3 bài toán nhị phân: A vs. B, A vs. C và B vs. C. Mỗi bài toán nhị phân sẽ quyết định lớp của một điểm dữ liệu. Lớp cuối cùng cho một điểm dữ liệu sẽ được xác định bằng cách đếm số lượng phiếu bầu cho mỗi lớp từ các bài toán nhị phân và chọn lớp có số phiếu bầu cao nhất.