III. Thuật toán AES - thực hiện (tiếp)

4. AddRoundKey

Trong suốt quá trình mã hóa và giải mã, AddRoundKey được thực hiện $11$ lần (đối với AES-128), và được thực hiện ngay trước khi đi vào các round mã hóa/giải mã, đồng thời được thực hiện cuối cùng trong mỗi round:

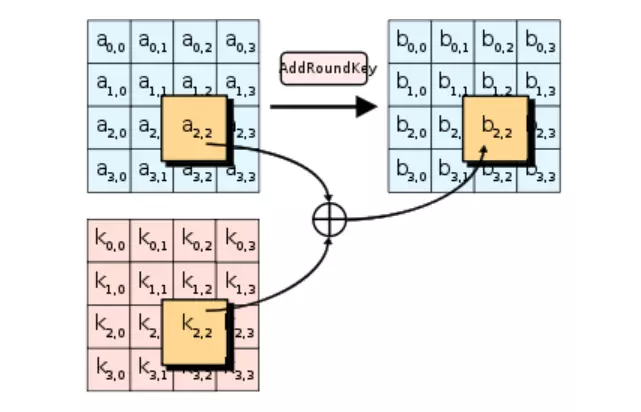
AddRoundKey sử dụng thuật toán XOR đối với state table hiện tại và nhóm secret key tương ứng với thứ tự lần thực hiện của AddRoundKey. Kết quả thu được một state table mới đưa vào sử dụng trong giai đoạn tiếp theo.

Tuy chỉ được thực hiện mã hóa đơn giản bằng cách sử dụng thuật toán XOR, nhưng AddRoundKey là công việc duy nhất trong $4$ công việc của quá trình mã hóa AES có sự tham gia của secret key. Bởi vậy, khi kẻ tấn công có được văn bản mã hóa nhưng không có thông tin về secret key sẽ vô cùng khó khăn để giải mã.

Chương trình Python minh họa thực hiện AddRoundKey (Challenge Round Keys):

state = [ [206, 243, 61, 34], [171, 11, 93, 31], [16, 200, 91, 108], [150, 3, 194, 51],
] round_key = [ [173, 129, 68, 82], [223, 100, 38, 109], [32, 189, 53, 8], [253, 48, 187, 78],
] def add_round_key(state, round_key): state_arr, round_key_arr, new_state_arr = [], [], [] for i in state: for j in i: state_arr.append(j) for i in round_key: for j in i: round_key_arr.append(j) for i in range(16): new_state_arr.append(state_arr[i] ^ round_key_arr[i]) return new_state_arr new_state_arr = add_round_key(state, round_key)
print(new_state_arr) # [99, 114, 121, 112, 116, 111, 123, 114, 48, 117, 110, 100, 107, 51, 121, 125]

Trước hết, chương trình lưu các phần tử trong hai ma trận state và round_key vào hai mảng, sau đó thực hiện XOR lần lượt từng phần tử tương ứng trong hai mảng này và lưu vào mảng new_state_arr. State table mới có thể thu được bằng cách chuyển các phần tử trong mảng new_state_arr vào ma trận $4\times 4$.

5. SubBytes

SubBytes là công việc được thực hiện ở đầu mỗi round, tổng thực hiện $10$ lần (xét AES-128). Đối với các round giải mã, chúng ta có InvSubBytes thực hiện ngược lại với SubBytes là công việc thứ hai trong mỗi round.

SubBytes sẽ thay thế mỗi phần tử trong state table hiện tại thành một phần tử tương ứng (ánh xạ 1-1) trong một mảng các phần tử cố định (Gọi là S-box). S-Box là một bảng $16\times 16$ các phần tử (thường được biểu diễn dưới dạng Hex):

hàng/cột	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0x63	0x7c	0x77	0x7b	0xf2	0x6b	0x6f	0xc5	0x30	0x01	0x67	0x2b	0xfe	0xd7	0xab	0x76
1	0xca	0x82	0xc9	0x7d	0xfa	0x59	0x47	0xf0	0xad	0xd4	0xa2	0xaf	0x9c	0xa4	0x72	0xc0
2	0xb7	0xfd	0x93	0x26	0x36	0x3f	0xf7	0xcc	0x34	0xa5	0xe5	0xf1	0x71	0xd8	0x31	0x15
3	0x04	0xc7	0x23	0xc3	0x18	0x96	0x05	0x9a	0x07	0x12	0x80	0xe2	0xeb	0x27	0xb2	0x75
4	0x09	0x83	0x2c	0x1a	0x1b	0x6e	0x5a	0xa0	0x52	0x3b	0xd6	0xb3	0x29	0xe3	0x2f	0x84
5	0x53	0xd1	0x00	0xed	0x20	0xfc	0xb1	0x5b	0x6a	0xcb	0xbe	0x39	0x4a	0x4c	0x58	0xcf
6	0xd0	0xef	0xaa	0xfb	0x43	0x4d	0x33	0x85	0x45	0xf9	0x02	0x7f	0x50	0x3c	0x9f	0xa8
7	0x51	0xa3	0x40	0x8f	0x92	0x9d	0x38	0xf5	0xbc	0xb6	0xda	0x21	0x10	0xff	0xf3	0xd2
8	0xcd	0x0c	0x13	0xec	0x5f	0x97	0x44	0x17	0xc4	0xa7	0x7e	0x3d	0x64	0x5d	0x19	0x73
9	0x60	0x81	0x4f	0xdc	0x22	0x2a	0x90	0x88	0x46	0xee	0xb8	0x14	0xde	0x5e	0x0b	0xdb
A	0xe0	0x32	0x3a	0x0a	0x49	0x06	0x24	0x5c	0xc2	0xd3	0xac	0x62	0x91	0x95	0xe4	0x79
B	0xe7	0xc8	0x37	0x6d	0x8d	0xd5	0x4e	0xa9	0x6c	0x56	0xf4	0xea	0x65	0x7a	0xae	0x08
C	0xba	0x78	0x25	0x2e	0x1c	0xa6	0xb4	0xc6	0xe8	0xdd	0x74	0x1f	0x4b	0xbd	0x8b	0x8a
D	0x70	0x3e	0xb5	0x66	0x48	0x03	0xf6	0x0e	0x61	0x35	0x57	0xb9	0x86	0xc1	0x1d	0x9e
E	0xe1	0xf8	0x98	0x11	0x69	0xd9	0x8e	0x94	0x9b	0x1e	0x87	0xe9	0xce	0x55	0x28	0xdf
F	0x8c	0xa1	0x89	0x0d	0xbf	0xe6	0x42	0x68	0x41	0x99	0x2d	0x0f	0xb0	0x54	0xbb	0x16

Quy tắc thay thế như sau: Đối với phần tử $0x\alpha\beta$ trong state table, chúng ta sẽ thay thế nó bằng phần tử hàng $\alpha$, cột $\beta$ trong bảng S-box. Ví dụ, với phần tử 0x4c, chúng ta tìm kiếm ở hàng $4$, cột $c$ trong S-box thu được 0x29 sẽ là giá trị thay thế.

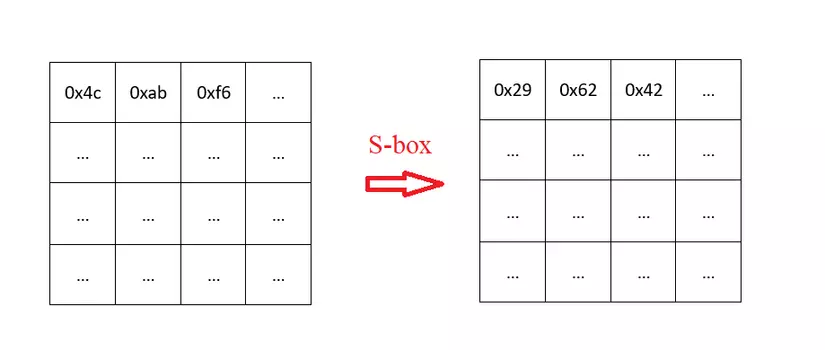
Tương tự, đối với InvSubBytes chính là tra cứu bảng Inv-S-box để thay thế ngược lại:

hàng/cột	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0x52	0x09	0x6a	0xd5	0x30	0x36	0xa5	0x38	0xbf	0x40	0xa3	0x9e	0x81	0xf3	0xd7	0xfb
1	0x7c	0xe3	0x39	0x82	0x9b	0x2f	0xff	0x87	0x34	0x8e	0x43	0x44	0xc4	0xde	0xe9	0xcb
2	0x54	0x7b	0x94	0x32	0xa6	0xc2	0x23	0x3d	0xee	0x4c	0x95	0x0b	0x42	0xfa	0xc3	0x4e
3	0x08	0x2e	0xa1	0x66	0x28	0xd9	0x24	0xb2	0x76	0x5b	0xa2	0x49	0x6d	0x8b	0xd1	0x25
4	0x72	0xf8	0xf6	0x64	0x86	0x68	0x98	0x16	0xd4	0xa4	0x5c	0xcc	0x5d	0x65	0xb6	0x92
5	0x6c	0x70	0x48	0x50	0xfd	0xed	0xb9	0xda	0x5e	0x15	0x46	0x57	0xa7	0x8d	0x9d	0x84
6	0x90	0xd8	0xab	0x00	0x8c	0xbc	0xd3	0x0a	0xf7	0xe4	0x58	0x05	0xb8	0xb3	0x45	0x06
7	0xd0	0x2c	0x1e	0x8f	0xca	0x3f	0x0f	0x02	0xc1	0xaf	0xbd	0x03	0x01	0x13	0x8a	0x6b
8	0x3a	0x91	0x11	0x41	0x4f	0x67	0xdc	0xea	0x97	0xf2	0xcf	0xce	0xf0	0xb4	0xe6	0x73
9	0x96	0xac	0x74	0x22	0xe7	0xad	0x35	0x85	0xe2	0xf9	0x37	0xe8	0x1c	0x75	0xdf	0x6e
A	0x47	0xf1	0x1a	0x71	0x1d	0x29	0xc5	0x89	0x6f	0xb7	0x62	0x0e	0xaa	0x18	0xbe	0x1b
B	0xfc	0x56	0x3e	0x4b	0xc6	0xd2	0x79	0x20	0x9a	0xdb	0xc0	0xfe	0x78	0xcd	0x5a	0xf4
C	0x1f	0xdd	0xa8	0x33	0x88	0x07	0xc7	0x31	0xb1	0x12	0x10	0x59	0x27	0x80	0xec	0x5f
D	0x60	0x51	0x7f	0xa9	0x19	0xb5	0x4a	0x0d	0x2d	0xe5	0x7a	0x9f	0x93	0xc9	0x9c	0xef
E	0xa0	0xe0	0x3b	0x4d	0xae	0x2a	0xf5	0xb0	0xc8	0xeb	0xbb	0x3c	0x83	0x53	0x99	0x61
F	0x17	0x2b	0x04	0x7e	0xba	0x77	0xd6	0x26	0xe1	0x69	0x14	0x63	0x55	0x21	0x0c	0x7d

Đối với thực hiện bước SubBytes trong lập trình, xin dành cho bạn đọc thử sức với challenge Confusion through Substitution.

6. ShiftRows

ShiftRows được thực hiện sau công việc SubBytes trong mỗi round, tổng $10$ lần (đối với AES-128). Đối với các round giải mã, chúng ta có InvShiftRows thực hiện ngược lại.

ShiftRows làm việc với mỗi hàng trong state table, trong đó thực hiện dịch chuyển vòng quanh các phần tử sang trái $i$ đơn vị đối với hàng $i$ (tính từ hàng $0$).

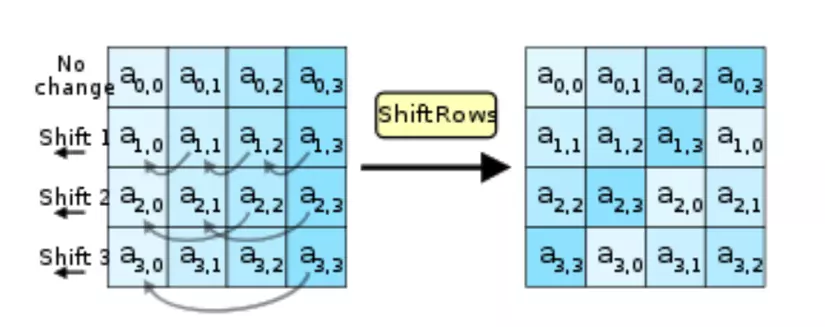
Chú ý thứ tự đã quy ước khi biểu diễn state table trong mảng hai chiều Python, chúng ta có hàm shift_rows() thực hiện như sau:

def shift_rows(s): s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1] s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2] s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]

Trong quá trình giải mã, InvShiftRows sẽ dịch chuyển vòng quanh các phần tử trong mỗi hàng của state table theo hướng ngược lại (dịch phải), số đơn vị dịch chuyển không đổi so với mã hóa. Dựa vào hàm shift_rows() trên, các bạn có thể viết lại hàm inv_shift_rows() nhé!

7. MixColumns

MixColumns có một điểm khác biệt với $3$ công việc còn lại là nó được thực hiện ít hơn một lần so với các giai đoạn khác, tổng $9$ lần (xét AES-128). Trong round cuối cùng của cả quá trình mã hóa và giải mã sẽ không thực hiện MixColumns và InvMixColumns.

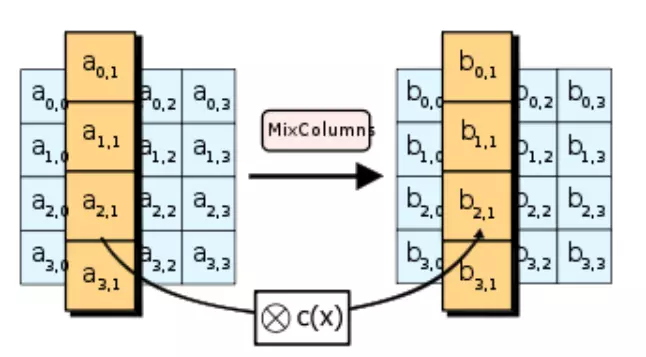
MixColumns được thực hiện thông qua một phép tính ma trận đặc biệt với ma trận:

\left[\begin{array}\\ 0x02 & 0x03 & 0x01 & 0x01\\ 0x01 & 0x02 & 0x03 & 0x01\\ 0x01 & 0x01 & 0x02 & 0x03\\ 0x03 & 0x01 & 0x01 & 0x02\\ \end{array}\right]

Tức là thu được ma trận mới thông qua phép tính:

\left[\begin{array}\\ S'_{0,0} & S'_{0,1} & S'_{0,2} & S'_{0,3}\\ S'_{1,0} & S'_{1,1} & S'_{1,2} & S'_{1,3}\\ S'_{2,0} & S'_{2,1} & S'_{2,2} & S'_{2,3}\\ S'_{3,0} & S'_{3,1} & S'_{3,2} & S'_{3,3}\\ \end{array}\right] \ =\ \left[\begin{array}\\ 0x02 & 0x03 & 0x01 & 0x01\\ 0x01 & 0x02 & 0x03 & 0x01\\ 0x01 & 0x01 & 0x02 & 0x03\\ 0x03 & 0x01 & 0x01 & 0x02\\ \end{array}\right] \left[\begin{array}\\ S_{0,0} & S_{0,1} & S_{0,2} & S_{0,3}\\ S_{1,0} & S_{1,1} & S_{1,2} & S_{1,3}\\ S_{2,0} & S_{2,1} & S_{2,2} & S_{2,3}\\ S_{3,0} & S_{3,1} & S_{3,2} & S_{3,3}\\ \end{array}\right]

Cách tính phần tử ở cột $j$ trong mỗi hàng như sau:

$$S'_{0,j}=(0x02\ *\ S_{0,j})\ +\ (0x03\ *\ S_{1,j})\ +\ (0x01\ *\ S_{2,j})\ +\ (0x01\ *\ S_{3,j})\\ S'_{1,j}=(0x01\ *\ S_{0,j})\ +\ (0x02\ *\ S_{1,j})\ +\ (0x03\ *\ S_{2,j})\ +\ (0x01\ *\ S_{3,j})\\ S'_{2,j}=(0x01\ *\ S_{0,j})\ +\ (0x01\ *\ S_{1,j})\ +\ (0x02\ *\ S_{2,j})\ +\ (0x03\ *\ S_{3,j})\\ S'_{3,j}=(0x03\ *\ S_{0,j})\ +\ (0x01\ *\ S_{1,j})\ +\ (0x01\ *\ S_{2,j})\ +\ (0x02\ *\ S_{3,j})\\$$

Như đã đề cập, phép tính ma trận trên đặc biệt bởi vì phép nhân và phép cộng ở đây là các phép toán được quy ước trong GF(2^8). Chúng ta sẽ cố gắng theo hướng tiếp cận đơn giản nhất đối với hai phép toán này.

Phép cộng ở đây chính là phép toán XOR bit, tức là $a + b = a \oplus b$.

Phép nhân sẽ mang tính phức tạp hơn, chúng ta đang xét với các số hạng có độ dài $8$ bit, chỉ cần tính được ba dạng phép tính $A\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0)$ với $A\in\{0x01;\ 0x02;\ 0x03\}$. Với $A = 0000\ 0001$, ta có:

$$(0000\ 0001)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0) = a_7a_6a_5a_4\ a_3a_2a_1a_0$$

Với $A = 0000\ 0010$, cách tính dựa trên giá trị của $a_7$:

$$(0000\ 0001)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0)= \begin{cases} a_6a_5a_4a_3\ a_2a_1a_00& \text{nếu }a_7=0\\ (a_6a_5a_4a_3\ a_2a_1a_00)\ \oplus (0001\ 1011)& \text{nếu }a_7=1 \end{cases}$$

Với $A = 0000\ 0011$, dựa trên phép toán XOR và tính chất kết hợp chúng ta có:

$\ \ \ \ (0000\ 0011)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0)$ $=[(0000\ 0010) \oplus (0000\ 0001)]\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0)$ $=[(0000\ 0010)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0) ]\oplus [(0000\ 0001)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0) ]$ $=[(0000\ 0010)\ * \ (a_7a_6a_5a_4\ a_3a_2a_1a_0) ]\oplus (a_7a_6a_5a_4\ a_3a_2a_1a_0)$

Biểu thức cuối có thể tính bình thường dựa trên các quy tắc trước.

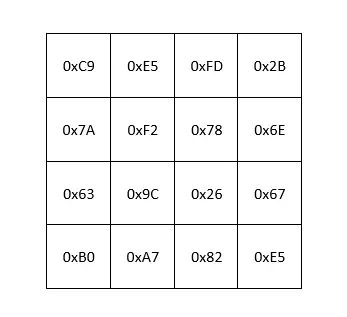
Bài tập dành cho bạn đọc, từ các công thức trên, hãy hoàn thiện quá trình MixColumns cho state table sau:

Tài liệu tham khảo

• https://en.wikipedia.org/wiki/Advanced_Encryption_Standard
• https://www.geeksforgeeks.org/advanced-encryption-standard-aes/
• https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf
• https://en.wikipedia.org/wiki/AES_key_schedule