Ở Việt Nam có một nghịch lý ai cũng biết: hầu hết sinh viên ngành CNTT đều đã học cấu trúc dữ liệu và giải thuật, thuộc các môn bắt buộc. Thế nhưng lại rất hiếm khi ứng dụng vào công việc hoặc bị loại ngay từ vòng test thuật toán, dù độ khó không cao. Đây là một thực tế buồn.
Rất nhiều công ty công nghệ yêu cầu ứng viên biết cấu trúc dữ liệu và giải thuật. Đa số sẽ dùng các bài test thuật toán để xem ứng viên có thực sự hiểu và ứng dụng được không.
Những công ty này sẽ có chuẩn mực chất lượng phần mềm rất cao, engineer của họ khi cần có thể lập trình được chứ không chỉ develop trên những cái có sẵn. Mặt khác, nó thể hiện tư duy lập trình và phát triển phần mềm của ứng viên, khả năng tiến xa và hiểu sâu các công nghệ của họ trong tương lai.
Trong bài viết này, 200Lab sẽ chia sẻ những trường hợp dễ thấy, thông dụng nhất để các bạn có thể dễ dàng sử dụng cấu trúc dữ liệu để tối ưu ứng dụng của bạn.
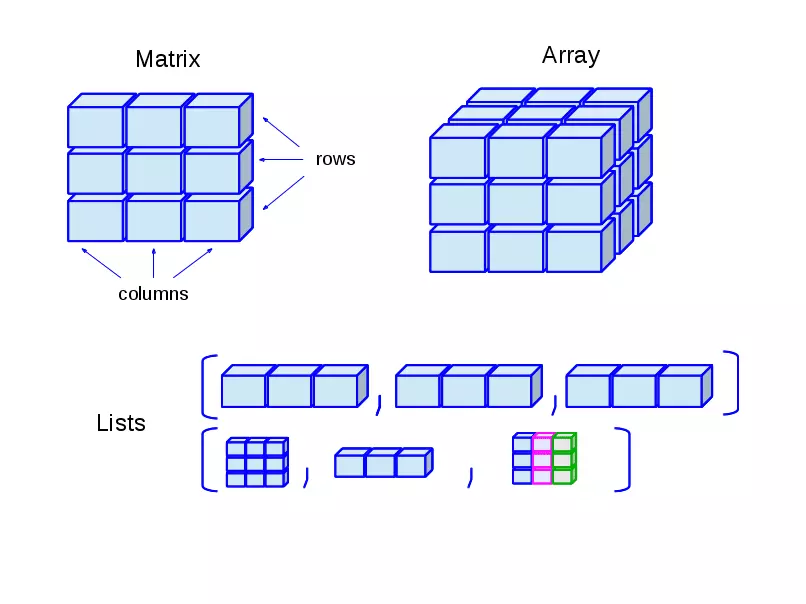
1. Tối ưu mảng 2 chiều với mảng 1 chiều
Nếu khi nào bạn có nhu cầu dùng mảng 2 chiều (hay còn được gọi là array chứa array) thì có thể nghĩ đến mảng 1 chiều là đủ.
Ví dụ: Gọi arr là mảng 2 chiều với 10 hàng 10 cột, i và j là index lần lượt ở hàng và cột (Row & Column). Từ đó truy xuất mảng sẽ có dạng arr[i][j].
Để tối ưu hơn: chúng ta chỉ cần 1 array có 10*10 = 100 phần tử là được. Khi đó vị trí ở (i,j) sẽ là 1 index duy nhất được tính như sau:
index = (i*10) + j
100 phần tử đặt liền kề nhau đương nhiên lý tưởng hơn nhiều!!
Lưu ý: một số ngôn ngữ sẽ cấp phát 10 array riêng lẻ (rời rạc, không liên tục trong dãy memory). Đây là lý do chúng ta cần vận dụng cách này.
Một ứng dụng hay thấy nhất là dữ liệu hình ảnh không bao giờ có [][]byte mà chỉ cần []byte thôi. Hoặc nếu các bạn làm game cờ caro, cờ tướng, cờ vua thì bàn cờ cũng có thể dùng mảng 1 chiều cũng được.
2. Tối ưu lưu trữ cho Color(Màu sắc) hoặc IP
Đối với database: Giả sử chúng ta có 10 triệu dòng dữ liệu, trong đó có thông tin màu sắc (red, green, blue) hoặc IPv4 (dạng a.b.c.d) thì sao nhỉ?
Có 2 cách lưu thường thấy: lưu 3 cột R,G và B hoặc 1 cột là string chứa dạng hex của màu (“ffeedd“).
Từ đó: nếu lưu 3 cột kiểu số nguyên ta mất ít nhất 4×3 =12 bytes. Còn nếu là String thì 1*6 = 6bytes (ít nhất).
Thực ra chúng ta chỉ cần 1 cột số nguyên (4 bytes) là đủ rồi. Vấn đề là làm sao để quy đổi thôi.
Nói về màu sắc. Ta có 3 channel, mỗi channel có độ lớn 8bit = 2^8 = 256 giá trị (0-255).
Mỗi màu có tổng độ lớn là 24bit. Các bạn có thể hiểu là 24 chữ số 0 và 1 liền kề nhau. Tức là 3 bytes thôi.
Cách đổi rất đơn giản là dùng các phép bitwise:
color = R << 16 | G << 8 | B
À… Mà nếu cần đổi ngược lại thì sao nhỉ:
R = color >> 16
G = color >> 8 & 0xff
B = color & 0xff
Tương tự các bạn có thể suy ra cách làm với IP4 mà đúng không?
Phương án này sẽ làm giảm rất đáng kể dung lương lưu trữ. Ngoài ra, nếu ta đánh index cho cột số nguyên thì sẽ luôn hiệu quả hơn rất nhiều so với đánh cho 3 cột hoặc cột string, tức là ta đã gián tiếp tăng tốc truy vấn. Sẽ có trường hợp các bạn truy vấn tìm màu giống nhau, nếu lưu String sẽ không thể làm được.
3. Linked List cho những thứ không cần truy xuất qua index hoặc có tần suất Remove/Add cao
200Lab có thể quả quyết hầu hết các bạn đọc luôn phân biệt được Array và Linked List khác nhau ở đâu vì đây là cấu trúc dữ liệu cơ bản được sử dụng thường xuyên.
Array: là một dãy bộ nhớ liên tục và cố định. Vì thế khi Add/Remove phần tử, các ngôn ngữ sẽ phải tạo cái mới. Ưu điểm: truy xuất với index nên sẽ rất nhanh O(1). Nhược điểm: việc chèn và xóa phần tử của mảng mất nhiều thời gian. Linked List: là một danh sách, một dãy bộ nhớ không liên tục được liên kết lại bởi con trỏ. Ưu điểm: khi add/remove thì chỉ cần thay đổi con trỏ thôi nên sẽ rất nhanh. Nhược điểm: tìm kiếm phần tử thì lại phải duyệt qua từng thành phần O(n), chậm hơn đáng kể. Okie trong trường dạy là thế nhưng có case nào đâu mà xài!! Thật ra là có, chỉ là chúng ta có muốn hay không thôi.
Hãy nghĩ về carousel component chúng ta thường dùng. Bình thường có lẽ chúng ta sẽ dùng Array cho tiện. Bây giờ các bạn có thể đổi lại với Linked-List. Khi đó nếu các bạn cần Add/Remove thì nhanh hơn nhiều. Với cả thật ra chúng ta chỉ dùng Next(), Prev() chứ rất hiếm khi đi thẳng tới một “index” nào đó.
Đặc biệt là nếu các bạn muốn danh sách dạng vòng tròn khép kín: đơn giản là nối “next” pointer đến phần tử đầu tiên của dãy.
Rất nhiều hiện thân của Linked-List: Transaction lưu các step thay đổi dữ liệu, cơ chế cấp phát bộ nhớ Linux, Blockchain (quá nổi tiếng),…
Tóm lại:
Nếu các bạn không hề dùng những thứ 200Lab kể trên, không sao hết, vì ứng dụng vẫn đang hoạt động bình thường. Còn nếu các bạn muốn tiến xa hơn, hoặc ứng tuyển và các công ty Big Tech thì có thể dành thời gian hơn cho chúng. Chúng cũng thú vị và có phần “xinh đẹp” đấy chứ.
Nguồn: https://edu.200lab.io/blog/cau-truc-du-lieu-toi-uu-ung-dung-cua-ban-nhu-the-nao