Bài viết trình bày về kiến trúc Transformer (Bộ chuyển đổi) từ những khái niệm và thành phần cơ bản nhất, với mong muốn giúp bạn đọc có thể nắm bắt được phương thức hoạt động của một mạng dựa trên Transformer và áp dụng kiến thức này vào nghiên cứu và xây dựng các mô hình tiên tiến gần đây.

Kiến trúc transformer được giới thiệu trong bài báo này vào năm 2017 như một công cụ cho quá trình tải nạp chuỗi (sequence transduction) - chuyển đổi một chuỗi ký tự thành chuỗi khác. Ví dụ phổ biến nhất của quá trình này là dịch thuật, như dịch tiếng Anh sang tiếng Đức. Transformer cũng đã được chỉnh sửa để thực hiện tác vụ hoàn thành chuỗi (sequence completion) - tức là từ 1 lệnh nhắc (có thể là một câu hoặc đoạn văn), viết tiếp đoạn văn đó theo cùng một phong cách viết. Chúng đã nhanh chóng trở thành một công cụ không thể thiếu trong nghiên cứu và phát triển sản phẩm trong xử lý ngôn ngữ tự nhiên.

Trước khi bắt đầu, tôi có một ghi chú nhỏ. Bạn sẽ thấy bài viết này nói nhiều về phép nhân ma trận và có cả phương pháp lan truyền ngược (backpropagation - giải thuật để huấn luyện mô hình), nhưng bạn không cần phải biết bất cứ thuật ngữ nào trước cả. Ta sẽ cùng thêm dần từng khái niệm mà chúng ta cần hiểu, kèm theo giải thích chi tiết.

Hiểu được transformer không phải là một hành trình ngắn, nhưng tôi hy vọng bạn sẽ học được nhiều điều khi đi trên hành trình này.

1. Mã hóa one-hot

Ngôn ngữ tự nhiên bao gồm các từ. Rất nhiều từ. Bước đầu tiên ta cần thực hiện là chuyển tất cả các từ về dạng số để có thể tính toán trên chúng.

Hãy tưởng tượng rằng mục tiêu của chúng ta là tạo ra một máy tính có thể phản hồi lại các lệnh bằng giọng nói của mình. Nhiệm vụ của chúng ta là xây dựng bộ biến đổi để chuyển đổi một chuỗi âm thanh thành một chuỗi từ.

Ta bắt đầu bằng cách chọn bộ từ vựng, là một bộ các ký tự mà tạo thành các chuỗi. Trong bài toán trên, ta sẽ có hai bộ ký tự khác nhau, một bộ đại diện cho chuỗi đầu vào biểu thị bằng âm thanh nói và một bộ đại diện cho chuỗi đầu ra biểu thị bằng các từ.

Bây giờ, hãy giả sử rằng chúng ta tương tác với chương trình máy tính này bằng tiếng Anh. Có hàng chục nghìn từ trong tiếng Anh và có thể vài nghìn thuật ngữ chuyên biệt về máy tính. Tổng hợp lại, ta có một bộ từ vựng có kích thước gần 100 nghìn từ. Một trong các cách để chuyển đổi từ thành số là bắt đầu đếm từng từ một và gán cho mỗi từ một chỉ số. Sau đó, một chuỗi từ có thể được biểu diễn dưới dạng một danh sách các số.

Ví dụ, hãy xem xét một bộ từ vựng với kích thước bằng ba: files, find, và my. Mỗi từ có thể được thay thế bằng một số, chẳng hạn files = 1, find = 2, và my = 3. Sau đó, câu "Find my files" ("Tìm tập tin của tôi"), bao gồm chuỗi các từ [ find, my, files ] có thể được biểu diễn bằng chuỗi các số [2, 3, 1].

Đây là một phương pháp hoàn toàn hợp lệ để chuyển đổi các từ thành số, nhưng trong thực tế là có một phương pháp khác dễ dàng hơn để máy tính tính toán, đó là mã hóa one-hot. Trong mã hóa one-hot, một từ được đại diện bởi một mảng gần như toàn số không, có cùng chiều dài với kích thước bộ từ vựng, và chỉ có một phần tử có giá trị là một. Mỗi phần tử trong mảng tương ứng với một ký tự riêng biệt.

Một cách khác để nghĩ về mã hóa one-hot là mỗi từ vẫn được gán một số riêng của nó, nhưng giờ đây số đó là một chỉ mục của một mảng. Hình dưới đây là ví dụ về bộ từ vựng trên được mã hoá one-hot.

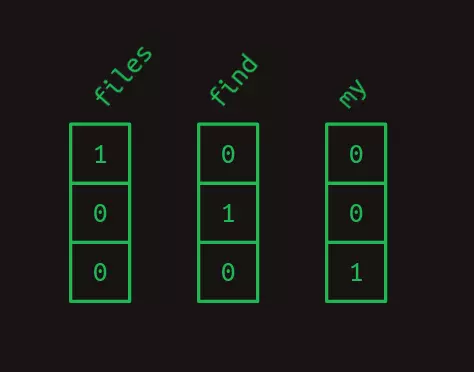
Vì vậy, câu "Find my files" trở thành một chuỗi các mảng một chiều, sau đó ta ghép chúng lại với nhau, câu trên trông giống như một mảng hai chiều.

Trong bài này, các khái niệm "mảng một chiều" và "vector" được sử dụng luân phiên nhau. Tương tự với 2 khái niệm "mảng hai chiều" và "ma trận".

Tích vô hướng

Một trong những lợi ích của biểu diễn one-hot là nó cho phép ta tính tích vô hướng. Phép này cũng được biết đến với tên gọi khác là tích nội. Để tính tích vô hướng hai vector, ta nhân từng phần tử tương ứng của chúng, sau đó cộng lại để thu được kết quả.

Các tích vô hướng đặc biệt hữu ích khi ta làm việc với các biểu diễn one-hot của các từ vựng. Tích vô hướng của bất kỳ vector one-hot nào với chính nó là bằng một.

Và tích vô hướng của 2 vector one-hot khác nhau bằng không.

Hai ví dụ trước cho thấy cách các tích vô hướng có thể được sử dụng để đo độ tương đồng giữa 2 từ. Trong một ví dụ khác, xét một vector đại diện cho sự kết hợp của nhiều từ với các trọng số khác nhau. Một từ được mã hóa one-hot có thể được so sánh với vector trọng số đó qua tích vô hướng để cho thấy từ đó được thể hiện mạnh mẽ như thế nào trong vector trọng số.

Nhân ma trận

Tích vô hướng là tiền đề của phép nhân ma trận, một phương pháp rất đặc biệt để kết hợp một cặp mảng hai chiều với nhau. Chúng ta sẽ gọi ma trận đầu tiên là A và ma trận thứ hai là B. Trong trường hợp đơn giản nhất, khi A chỉ có một hàng và B chỉ có một cột, kết quả của phép nhân ma trận là tích vô hướng của hai ma trận.

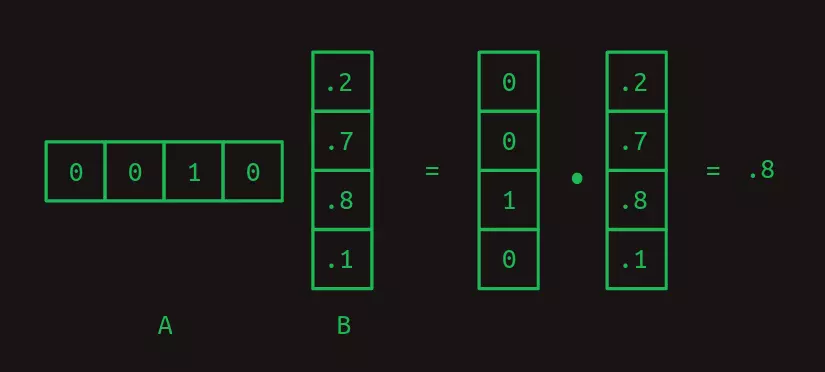
Chú ý rằng số cột của A và số hàng của B phải bằng nhau để hai mảng có số phần tử bằng nhau và nhờ đó mà phép tích vô hướng có thể được thực hiện thành công.

Khi A và B có kích thước lớn hơn, phép nhân 2 ma trận bắt đầu trở nên kỳ quặc. Để tính toán trên nhiều hàng của A hơn, ta tính tích vô hướng của B với từng hàng của A. Ma trận kết quả sẽ có số hàng bằng số hàng của A.

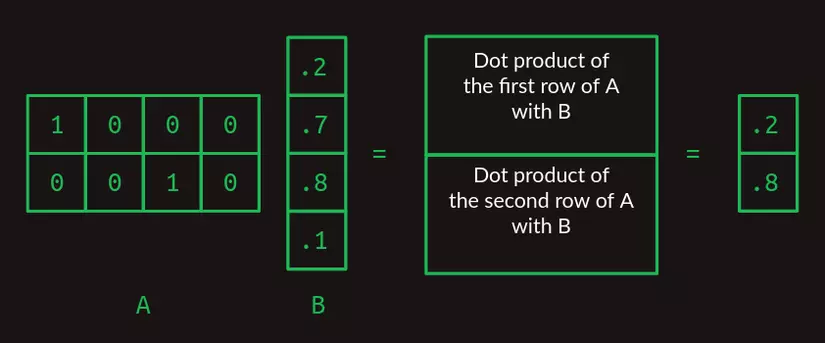
Khi B có nhiều cột hơn, ta tính tích vô hướng của từng cột với A và ghép kết quả lại theo từng cột tương ứng.

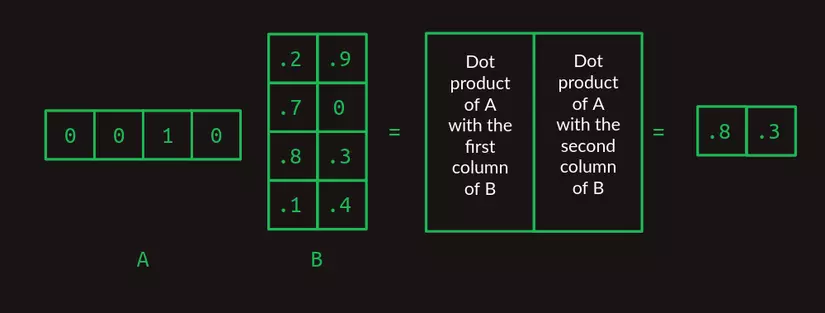
Lúc này, ta có thể mở rộng phép nhân với 2 ma trận bất kỳ, miễn là số cột của ma trận A bằng với số hàng của ma trận B. Ma trận kết quả sẽ có số hàng bằng với A, và số cột bằng với B.

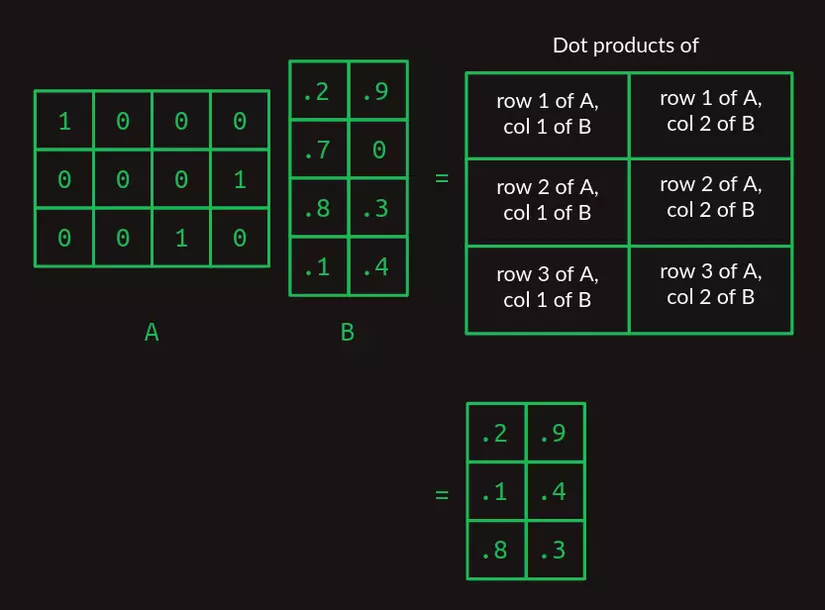
Nếu đây là lần đầu bạn nhìn thấy phép nhân ma trận, nó có thể trông hơi quá phức tạp so với cần thiết. Nhưng tôi đảm bảo rằng nó sẽ cần thiết ở các phần sau.

Nhân ma trận để tìm kiếm trong bảng

Chú ý rằng phép nhân ma trận ở ví dụ trên cũng hoạt động như một bảng tìm kiếm (lookup table). Ma trận A được tạo thành bởi một mảng các vector mã hoá one-hot, lần lượt có số 1 ở cột thứ nhất, cột thứ 4, và cột thứ 3. Kết quả của phép nhân hai ma trận lúc này sẽ gồm có lần lượt hàng đầu tiên, hàng thứ 4, và hàng thứ 3 của ma trận B.

Chính mẹo sử dụng các vector mã hoá one-hot để lấy từng hàng cụ thể của một ma trận là thành phần cốt lõi giúp transformer hoạt động.

Mô hình chuỗi bậc một

Ta có thể tạm thời gạt các ma trận sang một bên và quay lại vấn đề thực sự cần quan tâm, chuỗi các từ. Giả sử rằng ta bắt đầu xây dựng một giao diện xử lý ngôn ngữ tự nhiên, và ta muốn xử lý 3 câu lệnh khả dĩ sau:

Show me my directories please.
Show me my files please.
Show me my photos please.

Lúc này, bộ từ vựng sẽ gồm 7 từ:

{directories, files, me, my, photos, please, show}

Một cách hữu ích để biểu diễn các chuỗi này là sử dụng mô hình chuyển đổi (transition model). Đối với mỗi từ trong bộ từ vựng, đồ thị sẽ cho biết từ tiếp theo có khả năng là từ nào. Nếu người dùng hỏi về photos phân nửa các lần, 30% là hỏi về files, và còn lại là hỏi về directories, mô hình chuyển đổi sẽ trông như thế này. Tổng của các chuyển đổi từ một từ bất kỳ sẽ luôn bằng một.

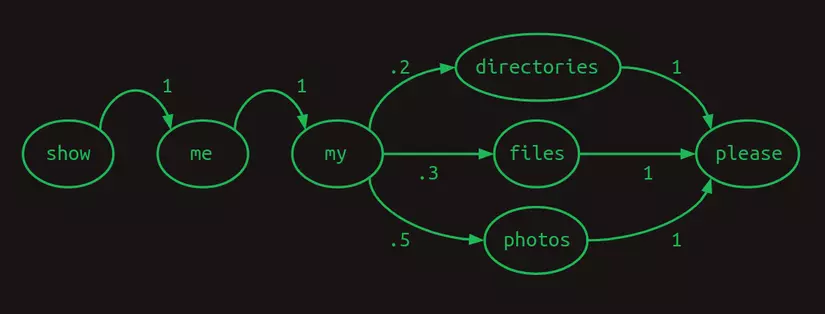
Mô hình chuyển đổi trên còn có thể được gọi là một chuỗi Markov vì nó thoả mãn tính chất Markov rằng xác suất của từ tiếp theo chỉ phụ thuộc vào các từ trước nó. Cụ thể hơn, đây là mô hình Markov bậc một vì một từ chỉ phụ thuộc vào từ ngay trước nó. Nếu nó xem xét 2 từ trước, mô hình sẽ trở thành mô hình Markov bậc 2.

Quay trở lại với ma trận. Các chuỗi Markov có thể được biểu diễn dưới dạng các ma trận để thuận tiện cho tính toán. Ta vẫn sẽ sử dụng quy tắc đánh số các từ như ở trên, với mỗi hàng thể hiện 1 từ trong bộ từ vựng. Các cột cũng tương tự như vậy. Mô hình chuyển đổi coi ma trận này là một bảng tìm kiếm để tìm hàng tương ứng với từ mà mô hình cần. Các giá trị trong từng cột là xác suất mà từ đó sẽ xuất hiện tiếp theo. Do là giá trị xác suất, các giá trị trong ma trận sẽ nằm trong khoảng từ 0 đến 1. Và do xác suất các khả năng của một sự kiện luôn có tổng bằng 1, tổng các giá trị trong cùng hàng luôn bằng 1.

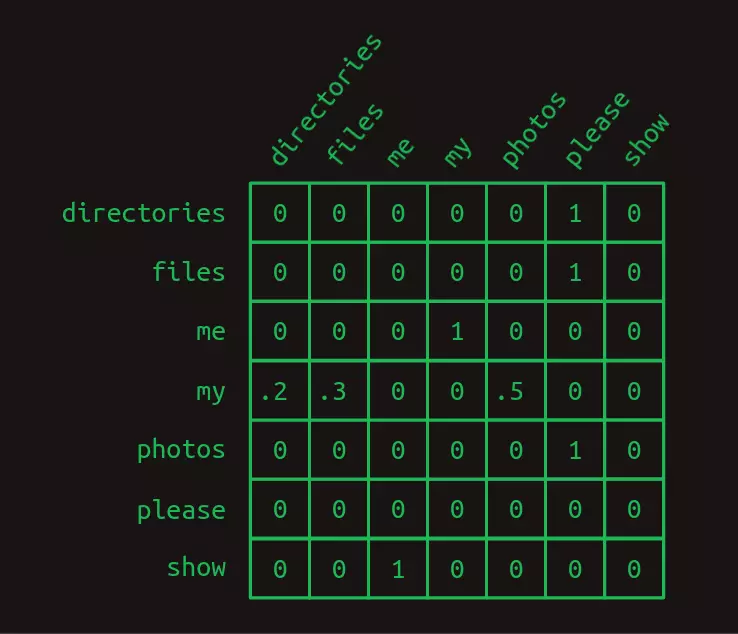
Trong ma trận chuyển đổi trên, ta có thể thấy cấu trúc của 3 câu lệnh khá rõ ràng. Hầu hết các xác suất chuyển đổi đều bằng 0 hoặc 1. Chỉ có một vị trí trong chuỗi Markov có hiện tượng rẽ nhánh. Sau từ my, các từ directories, files, hoặc photos đều có thể xuất hiện với các xác suất khác nhau. Ta không thể chắc chắn rằng từ nào sẽ xuất hiện, sự chắc chắn đó được thể hiện bởi các giá trị 0 và 1 trong ma trận.

Ta có thể sử dụng phép nhân ma trận với vector one-hot để thu được các xác suất chuyển đổi của một từ nhất định. Ví dụ, nếu ta muốn biết các xác suất của các từ sẽ xuất hiện sau my, ta có thể nhân ma trận mã hoá one-hot của từ my với ma trận chuyển đổi. Kết quả thu được sẽ là hàng thể hiện phân phối xác suất của từ nào sẽ xuất hiện tiếp theo.

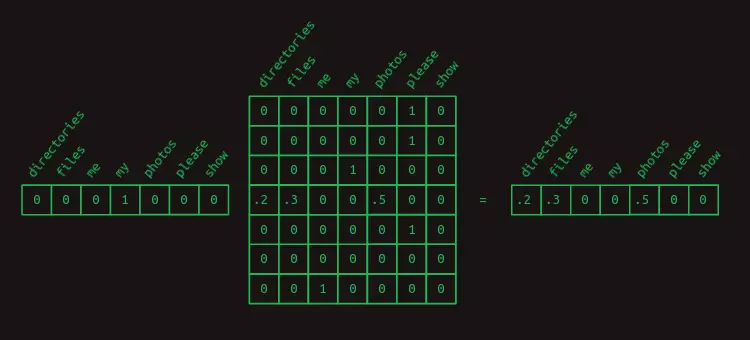
Mô hình chuỗi bậc hai

Dự đoán từ tiếp theo dựa trên từ hiện có là việc rất khó. Nó giống như dự đoán nguyên một giai điệu ngay khi nghe nốt nhạc đầu tiên. Việc này sẽ dễ dàng hơn đôi chút nếu ta có ít nhất 2 nốt nhạc để đoán.

Ta có thể mô phỏng lại trường hợp này qua một mô hình ngôn ngữ nhỏ trong chương trình máy tính. Chương trình sẽ chỉ nhận 2 câu sau làm đầu vào, với tỉ lệ 40/60.

Check whether the battery ran down please.
Check whether the program ran please.

Dạng chuỗi Markov có thể được minh hoạ theo dạng mô hình bậc một như hình sau.

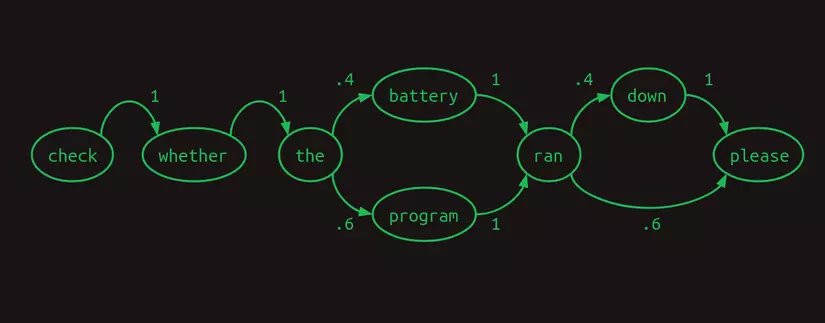
Từ hình trên ta có thể thấy rằng nếu mô hình dựa vào hai từ gần nhất để dự đoán từ tiếp theo, nó có thể hoạt động tốt hơn nhiều. Khi gặp cụm battery ran, mô hình sẽ biết chắc rằng từ tiếp theo sẽ là down, và khi gặp cụm program ran thì từ tiếp theo sẽ là please. Cách này sẽ giúp loại bỏ một nhánh của mô hình, giảm sự bất định và tăng độ tin cậy. Việc xét hai từ khiến mô hình trở thành mô hình Markov bậc hai, với nhiều thông tin ngữ cảnh hơn để dự đoán từ tiếp theo. Không dễ để vẽ mô hình Markov bậc 2, nhưng ta có thể thể hiện sự chuyển đổi như sau.

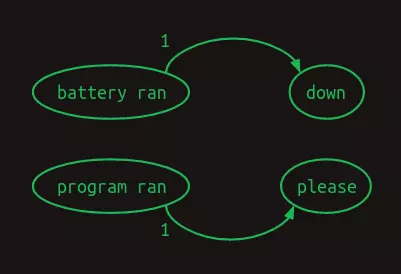
Để thể hiện sự khác biệt giữa 2 dạng mô hình, sau đây là ma trận chuyển đổi bậc một,

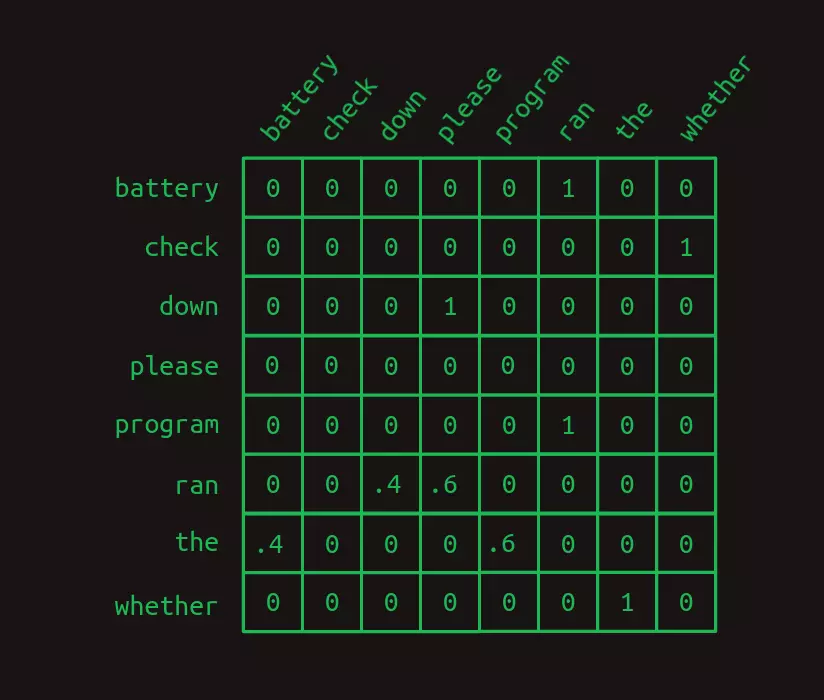
và đây là ma trận chuyển đổi bậc hai.

Chú ý rằng ma trận bậc hai có các hàng tương ứng với các cách ghép 2 từ với nhau (đa phần không được ghi rõ trong hình). Có nghĩa là nếu ta có bộ từ vựng với kích thước $N$ thì ma trận chuyển đổi sẽ có $N^2$ hàng.

Ưu điểm của việc này nằm ở độ tin cậy cao hơn. Có nhiều số 0 và 1 hơn và ít các số thập phân hơn ở mô hình bậc hai. Chỉ có duy nhất 1 hàng có chứa giá trị thập phân, tức là mô hình chỉ có 1 nhánh. Tóm lại, khi dùng hai từ thay vì 1 từ thì mô hình sẽ có nhiều ngữ cảnh, nhiều thông tin hơn để đoán từ tiếp theo.

Mô hình chuỗi bậc hai với skip

Mô hình bậc hai hoạt động tốt khi tả chỉ cần dựa vào 2 từ trước đó để quyết định từ tiếp theo sẽ là gì. Nhưng sẽ thế nào nếu ta phải dựa vào nhiều từ hơn? Giả sử rằng mô hình ngôn ngữ ta đang xây dựng có thể nhận vào 2 câu lệnh sau, với tỉ lệ là như nhau.

Check the program log and find out whether it ran please.
Check the battery log and find out whether it ran down please.

Trong ví dụ này, để quyết định từ nào sẽ xuất hiện sau từ ran, ta cần phải dựa vào 8 từ trước đó. Nếu ta muốn cải thiện mô hình bậc hai, tất nhiên ta có thể cân nhắc sử dụng mô hình bậc ba hoặc bậc cao hơn nữa. Tuy nhiên, với một bộ tự vựng lớn, mô hình bậc cao sẽ cần nhiều cách ghép từ hơn và phải brute-force để tìm kết quả. Đương nhiên ta có thể sử dụng mô hình bậc 8 với $N^8$ hàng, nhưng con số này sẽ là quá lớn với bất kỳ một bộ từ vựng thực tế nào.

Thay vào đó, ta có thể xây dựng một mô hình bậc hai, nhưng chỉ xét sự kết hợp của từ hiện tại với từng từ đã xuất hiện trước đó. Đây vẫn là mô hình bậc 2 vì ta chỉ xét hai từ một lúc, nhưng mô hình có thể nhìn xa hơn và xét tới sự phụ thuộc của từ hiện tại với các từ xuất hiện xa trước đó. Sự khác biệt giữa mô hình bậc hai có skip và một mô hình bậc cao thông thường là mô hình có skip bỏ qua phần lớn thông tin giữa từ đang xét và từ bậc cao. Tuy nhiên, chỉ cần giữ lại 2 từ thôi là ta đã có rất nhiều thông tin rồi.

Lúc này ta không thể sử dụng mô hình chuỗi Markov để minh hoạ nữa, nhưng ta vẫn có thể biểu diễn mối liên kết giữa các cặp từ ghép bởi từ đang xét và các từ trước đó như sau. Trong hình này, ta bỏ qua thể hiện trọng số bằng số, mà thay vào đó sử dụng độ đậm của mũi tên để thể hiện trọng số, với đường mũi tên càng đậm thì trọng số càng lớn.

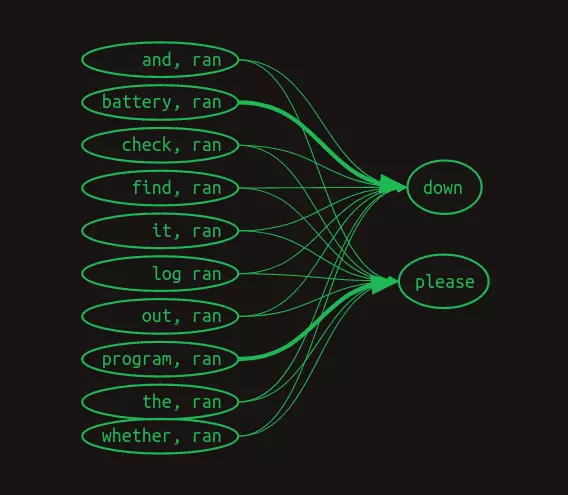
Ma trận chuyển đổi của mô hình này có dạng như sau.

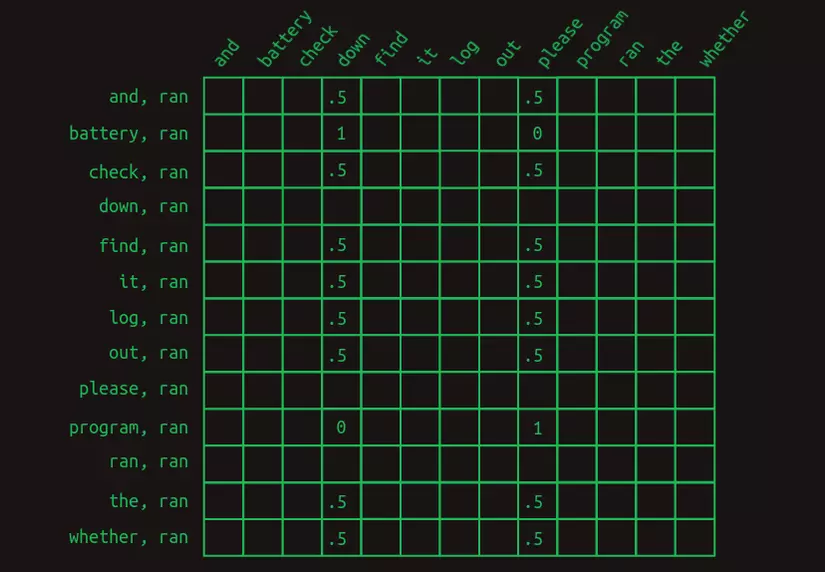
Hình trên chỉ hiển thị các hàng cần để dự đoán từ xuất hiện sau từ ran. Lần lượt các hàng xét từng trường hợp mà mỗi từ trong bộ từ vựng được đặt trước từ hiện tại (ran). Chỉ các giá trị cần để dự đoán được hiển thị. Tất cả các ô trống đều có giá trị bằng không.

Lúc này khi dự đoán từ xuất hiện sau từ ran, rõ ràng là ta không chỉ nhìn vào một hàng nữa, mà là cả một tập hợp các hàng. Bài toán lúc này đã đi xa khỏi vương quốc Markov. Mỗi hàng không còn đại diện cho trạng thái của chuỗi tại một điểm cụ thể nữa, mà thay vào đó, mỗi hàng đại diện cho một trong những đặc trưng (feature) có thể mô tả chuỗi tại một điểm cụ thể. Sự kết hợp của từ gần nhất với từng từ xuất hiện trước đó tạo thành một tập hợp các hàng khả dụng. Do sự thay đổi về ý nghĩa này, mỗi giá trị trong ma trận không còn đại diện cho một giá trị xác suất, mà thay vào đó là một lá phiếu bầu. Các phiếu bầu sẽ được tổng hợp và so sánh để xác định từ tiếp theo.

Hơn nữa, có thể thấy rằng hầu hết các đặc trưng đều không quan trọng. Đa phần các từ xuất hiện trong cả hai câu lệnh khả dĩ, và vì vậy việc chúng được xét đến không giúp ích gì cho việc dự đoán điều gì sẽ xảy ra tiếp theo. Tất cả chúng đều có giá trị là 0,5. Hai ngoại lệ duy nhất là battery và program, chúng có thể có trọng số 1 và 0. Đặc trưng (battery, ran) cho thấy ran là từ gần nhất và battery đã được sử dụng ở đâu đó trong câu. Đặc trưng này có trọng số 1 tại cột down và trọng số 0 tại cột please. Tương tự, đặc trưng (program, ran) có tập trọng số ngược lại. Cấu trúc này cho thấy rằng chính sự hiện diện của hai từ này trong câu, battery và program, có ý nghĩa quyết định trong việc dự đoán từ tiếp theo.

Để đưa từ tập các đặc trưng ghép bởi 2 từ thành ước lượng từ tiếp theo, ta cần tính tổng tất cả các hàng có liên quan. Sau khi tính tổng các, chuỗi Check the program log and find out whether it ran có tổng bằng 0 tại tất cả các cột, trừ cột down cho giá trị 4 và cột please cho giá trị 5. Chuỗi Check the battery log and find out whether it ran cũng vậy, trừ cột down cho giá trị 5 và cột please cho giá trị 4. Bằng cách chọn từ có tổng số phiếu bầu cao nhất làm dự đoán từ tiếp theo, mô hình này cho chúng ta câu trả lời đúng, mặc dù phụ thuộc vào tới tám từ.

Masking

Khi xem xét cẩn thận hơn, cách tính toán như trên có phần không thoả đáng. Sự khác biệt giữa tổng số phiếu bầu giữa 4 và 5 là tương đối nhỏ, cho thấy rằng rằng mô hình không thực sự tự tin. Và trong một mô hình ngôn ngữ lớn hơn, tự nhiên hơn, một sự khác biệt nhỏ như vậy có thể bị trung hoà bởi nhiễu thống kê.

Ta có thể làm nổi bật dự đoán bằng cách loại bỏ tất cả các phiếu bầu của các đặc trưng không có giá trị. Ngoại trừ battery, ran và program, ran. Lúc này, hãy nhớ rằng chúng ta lấy các hàng có liên quan ra khỏi ma trận chuyển đổi bằng cách nhân nó với một vector chỉ thị các đặc trưng nào là cần thiết. Đối với ví dụ này, ta đã sử dụng vector đặc trưng sau.

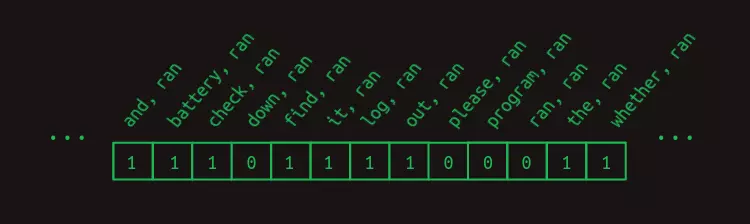
Vector đặc trưng có các phần tử c ó giá trị bằng một tại các đặc trưng là sự kết hợp của ran với mỗi từ đứng trước nó. Bất kỳ từ nào xuất hiện sau nó sẽ không được đưa vào bộ đặc trưng. (Trong bài toán dự đoán từ tiếp theo, những từ này chưa được nhìn thấy và vì vậy sẽ không công bằng nếu sử dụng chúng để dự đoán từ tiếp theo.) Hình minh hoạ không trình bày tất cả các tổ hợp từ khả dĩ khác, nhưng ta có thể bỏ qua chúng trong ví dụ này vì tất cả nhưng tổ hợp không được thể hiện đều bằng không.

Để cải thiện kết quả, ta cũng có thể buộc các tính năng không hữu ích về 0 bằng cách xây dựng một vector mặt nạ (mask). Đó là một vector mà các vị trí ta muốn ẩn hoặc che đi được đặt thành 0. Trong trường hợp trên, ta muốn bỏ qua mọi đặc trưng ngoại trừ cặp battery, run, và cặp program, run, hai đặc trưng có ích duy nhất.

Để áp dụng vector mặt nạ, ta nhân từng phần tử hai vector. Các đặc trưng tại vị trí không bị che thì sẽ được nhân với 1 và không thay đổi. Còn các đặc trưng tại vị trí không bị che thì sẽ được nhân với 0 và do đó buộc mang giá trị 0.

Vector mặt nạ có tác dụng che đi rất nhiều phần trong ma trận chuyển tiếp. Nó che giấu sự kết hợp của run với mọi từ khác ngoại trừ battery và program, chỉ để lại các đặc trưng quan trọng.

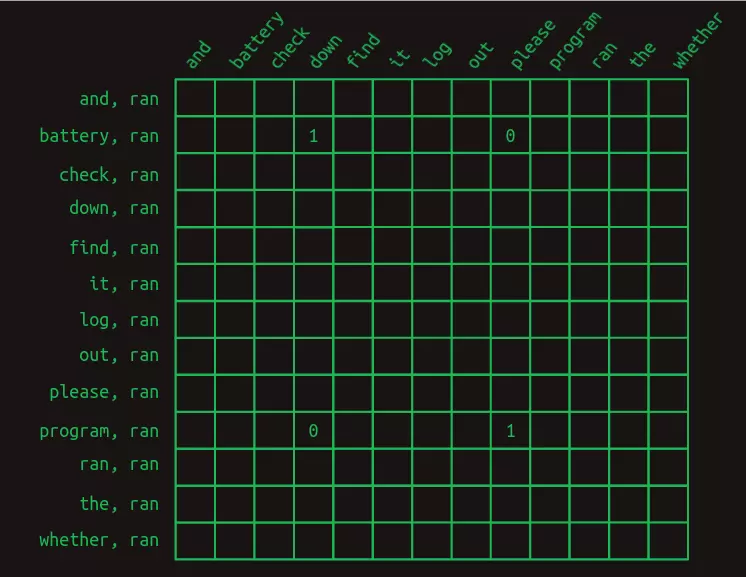
Sau khi che các đặc trưng không hữu ích, việc đưa ra dự đoán từ tiếp theo trở nên đáng tin cậy hơn nhiều. Khi từ battery xuất hiện trước đó trong câu, từ sau ran được dự đoán là down với trọng số là 1 và please với trọng số là 0. Chênh lệch trọng số 25% trước đây đã trở thành chênh lệch vô cực. Dự đoán đáng tin cậy tương tự cũng xảy ra đối với please khi program xuất hiện trước.

Quá trình che giấu có chọn lọc này được gọi là attention - tập trung trong tiêu đề của bài báo gốc về transformer. Đến lúc này, những gì ta mô tả về tầng tập trung chỉ là một dạng gần đúng. Các khái niệm quan trọng thì tương tự, nhưng các chi tiết về cách thức tầng tập trung được triển khai trong bài báo thì khác. Ta sẽ dần thu hẹp khoảng cách đó sau.

Tạm kết

Chúc mừng bạn đọc đến cuối phần 1 bài viết này. Bạn có thể dừng lại nếu bạn muốn. Mô hình chọn lọc bậc hai với skip là một phương pháp hữu ích để bắt đầu suy ngẫm về những gì transformer có thể thực hiện, ít nhất là ở phía bộ giải mã. Nó nắm bắt, một cách gần đúng, cách những mô hình ngôn ngữ tổng quát như GPT-3 của OpenAI hoạt động. Ta không kể toàn bộ câu chuyện, nhưng phần này là đủ để đại diện cho những ý trọng tâm.

Các phần tiếp theo sẽ thu hẹp khoảng cách giữa giải thích trực quan này và cách transformer được lập trình. Những điều này chủ yếu được thúc đẩy bởi ba điều kiện trong thực tế.

1. Máy tính đặc biệt giỏi trong phép nhân ma trận. Có cả một ngành công nghiệp xung quanh việc xây dựng phần cứng máy tính dành riêng cho phép nhân ma trận nhanh. Bất kỳ phép toán nào có thể được biểu diễn dưới dạng phép nhân ma trận đều có thể được thực hiện hiệu quả một cách đáng kinh ngạc. Giống như một con tàu cao tốc vậy, nếu bạn có thể chất hành lý của mình vào đó, nó sẽ đưa bạn đến nơi bạn muốn rất nhanh.
2. Mỗi bước đều cần phải khả vi. Trong bày này, ta chỉ đang làm việc với các ví dụ đơn giản và thoải mái chọn thủ công tất cả các xác suất chuyển đổi và giá trị vector mặt nạ - các tham số mô hình. Trong thực tế, những điều này phải được học thông qua lan truyền ngược (backpropagation), điều này phụ thuộc vào từng bước tính toán phải khả vi. Điều này có nghĩa là đối với bất kỳ thay đổi nhỏ nào trong một tham số, chúng ta có thể tính toán sự thay đổi tương ứng trong sai số hoặc mất mát của mô hình.
3. Gradient cần phải mịn và có điều kiện tốt. Sự kết hợp của tất cả các đạo hàm cho tất cả các tham số là gradient của hàm mất mát. Trong thực tế, gradient này cần phải mịn để lan truyền ngược hoạt động tốt, nghĩa là gradient không thay đổi quá nhanh khi ta di chuyển với các bước nhỏ theo bất kỳ hướng nào. Chúng cũng hoạt động tốt hơn nhiều khi gradient được điều chỉnh tốt, nghĩa là nó không lớn hơn về mặt cơ bản theo hướng này so với hướng khác. Nếu hình dung một hàm mất mát như một vùng địa hình, thì vườn quốc gia Grand Canyon sẽ là một nơi có điều kiện kém. Tùy thuộc vào việc bạn đang đi dọc phía dưới hay đi lên theo 1 hướng, bạn sẽ trải nghiệm những độ dốc rất khác nhau. Ngược lại, những ngọn đồi thoai thoải của hình nền Windows cổ điển sẽ có gradient trong điều kiện tốt.

Nếu khoa học về kiến trúc mạng lưới thần kinh đang tạo ra các khối xây dựng khác nhau, thì nghệ thuật sẽ là xếp chồng các khối sao cho gradient không thay đổi quá nhanh và có độ lớn gần như bằng nhau theo mọi hướng.