Bài viết này giải thích các yếu tố quyết định hiệu quả của quá trình xử lý song song, đưa chúng vào bối cảnh lịch sử và kỹ thuật. Sự hiểu biết về các yếu tố này cung cấp nền tảng để sử dụng tối ưu thư viện Streams để thực thi song song — và phần tiếp theo tập trung vào việc áp dụng trực tiếp các nguyên tắc này cho Streams.

Nhiều core hơn, không phải core nhanh hơn

Vào khoảng năm 2002, các kỹ thuật mà các nhà thiết kế chip đã sử dụng để mang lại hiệu suất tăng theo cấp số nhân đã bắt đầu cạn kiệt. Việc tăng tốc độ xung nhịp hơn nữa là không thực tế vì nhiều lý do, bao gồm tiêu thụ điện năng và tản nhiệt, đồng thời các kỹ thuật để thực hiện nhiều công việc hơn trên mỗi chu kỳ instruction-level parallelism) cũng đã bắt đầu đạt đến điểm giảm dần.

Định luật Moore dự đoán rằng số lượng bóng bán dẫn có thể được đóng gói trên một cùng một khuôn sẽ tăng gấp đôi sau mỗi hai năm. Khi các nhà thiết kế chip đạt đến frequency wall(bức tường tần số) vào năm 2002, đó không phải là vì Định luật Moore đã hết hiệu lực; chúng ta tiếp tục chứng kiến sự tăng trưởng ổn định theo cấp số nhân về số lượng bóng bán dẫn. Nhưng trong khi khả năng khai thác quỹ bóng bán dẫn ngày càng tăng này vào các lõi nhanh hơn đã hết tác dụng, các nhà thiết kế chip vẫn có thể sử dụng quỹ bóng bán dẫn ngày càng tăng này để đặt nhiều lõi hơn trên một khuôn đơn. Hình 1 minh họa xu hướng này với dữ liệu từ bộ xử lý Intel, được vẽ trên thang log. Đường trên cùng (thẳng) biểu thị sự tăng trưởng theo cấp số nhân về số lượng bóng bán dẫn, trong khi các đường biểu thị tốc độ xung nhịp, mức tiêu thụ năng lượng và instruction-level parallelism ở mức hướng dẫn đều cho thấy sự chững lại rõ ràng vào khoảng năm 2002.

Hình 1. Số lượng bóng bán dẫn và hiệu suất CPU cho CPU Intel (nguồn hình ảnh: Herb Sutter)

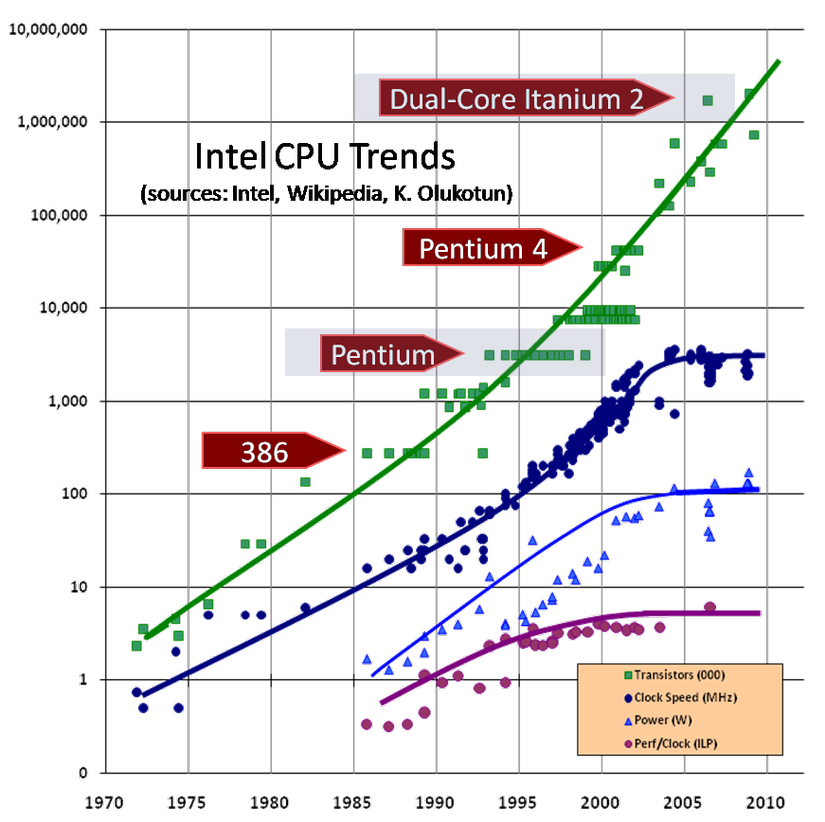
Có nhiều lõi hơn có thể mang lại hiệu quả năng lượng cao hơn (các lõi không được sử dụng tích cực có thể được tắt nguồn một cách độc lập), nhưng điều đó không nhất thiết đồng nghĩa với hiệu suất chương trình tốt hơn — trừ khi chúng ta có thể giữ cho tất cả các lõi bận rộn với công việc hữu ích. Thật vậy, các con chip ngày nay không cung cấp cho chúng ta nhiều lõi như định luật Moore cho phép — phần lớn là do phần mềm ngày nay không thể khai thác chúng một cách hiệu quả.

Từ concurrent tới parallel

Trong suốt phần lớn lịch sử điện toán, mục tiêu của concurrency(đồng thời) phần lớn không thay đổi — cải thiện hiệu suất bằng cách tăng mức sử dụng CPU — nhưng các kỹ thuật (và thước đo hiệu suất) đã thay đổi. Vào thời của các hệ thống lõi đơn, concurrency chủ yếu là về asynchrony(tính không đồng bộ)—cho phép một hoạt động không chiếm giữ CPU trong khi chờ I/O hoàn tất. Tính không đồng bộ có thể cải thiện cả responsiveness(khả năng phản hồi) (không đóng băng giao diện người dùng trong khi hoạt động nền đang diễn ra) và throughput(băng thông) (cho phép hoạt động khác sử dụng CPU trong khi chờ I/O hoàn tất). Trong một số mô hình concurrency (ví dụ: Các tác nhân và Communicating Sequential Processes - Tiến trình giao tiếp tuần tự [CSP]), mô hình đồng thời đã đóng góp vào cấu trúc của chương trình, nhưng đối với hầu hết các phần (dù tốt hơn hay xấu hơn), chúng ta chỉ sử dụng concurrency khi cần thiết cho hiệu suất.

Khi chúng ta chuyển sang kỷ nguyên đa lõi, ứng dụng chính của concurrency là phân tích khối lượng công việc thành các tác vụ chi tiết, độc lập — chẳng hạn như user requests — với mục đích băng thông bằng cách xử lý đồng thời nhiều yêu cầu. Vào khoảng thời gian này, các thư viện Java đã có các công cụ như thread pools, semaphores và futures, rất phù hợp với concurrency dựa trên tác vụ.

Tuy nhiên, khi số lượng lõi tiếp tục tăng, có thể không có đủ các tác vụ "xảy ra tự nhiên" để giữ cho tất cả các lõi bận rộn. Với nhiều lõi khả dụng hơn các tác vụ, một mục tiêu hiệu suất khác trở nên hấp dẫn: giảm latency(độ trễ) bằng cách sử dụng nhiều lõi để hoàn thành một tác vụ đơn lẻ nhanh hơn. Không phải tất cả các nhiệm vụ đều dễ dàng tuân theo kiểu phân tách này; những truy vấn hoạt động tốt nhất là các truy vấn chuyên sâu về dữ liệu trong đó các thao tác tương tự được thực hiện trên một tập dữ liệu lớn.

Đáng buồn thay, các thuật ngữ concurrency(đồng thờii) và parallelism(song song) không có định nghĩa tiêu chuẩn và chúng thường được sử dụng thay thế cho nhau (một cách nhầm lẫn). Về mặt lịch sử, tính concurrency mô tả tính chất của một program— mức độ mà chương trình được cấu trúc như là sự tương tác của các hoạt động tính toán hợp tác — trong khi tính parallelism là thuộc tính của việc program's execution(thực thi chương trình), mô tả mức độ mà mọi thứ thực sự xảy ra đồng thời. (Theo định nghĩa này, concurrency là khả năng xảy ra song song.) Sự khác biệt này rất hữu ích khi thực thi đồng thời thực sự chủ yếu là mối quan tâm về mặt lý thuyết, nhưng nó đã trở nên ít hữu ích hơn theo thời gian.

Các chương trình giảng dạy hiện đại hơn mô tả concurrency là kiểm soát quyền truy cập vào các tài nguyên được chia sẻ một cách chính xác và hiệu quả, trong khi parallelism là sử dụng nhiều tài nguyên hơn để giải quyết vấn đề nhanh hơn. Xây dựng cấu trúc dữ liệu thread-safe là domain của concurrency, được kích hoạt bởi các primitives như locks, events, semaphores, coroutines, hoặc software transactional memory(STM). Mặt khác, tính song song parallelism sử dụng các kỹ thuật như phân vùng hoặc phân đoạn để cho phép nhiều hoạt động đạt được tiến độ trong nhiệm vụ mà không cần phối hợp.

Tại sao sự khác biệt này lại quan trọng? Rốt cuộc, concurrency và parallelism có mục tiêu chung là hoàn thành nhiều việc cùng một lúc. Nhưng có một sự khác biệt lớn về mức độ dễ dàng của cả hai để đi đúng hướng. Làm cho concurrent code chính xác với các primitives phối hợp như locks là khó khăn, dễ bị lỗi và không tự nhiên. Làm cho mã song song đúng bằng cách sắp xếp rằng mỗi worker có phần vấn đề riêng để giải quyết tương đối đơn giản hơn, an toàn hơn và tự nhiên hơn.

Parallelism

Trong khi cơ chế song song thường đơn giản, phần khó là biết khi nào nên sử dụng nó. Parallelism hoàn toàn là một tối ưu hóa; đó là lựa chọn sử dụng nhiều tài nguyên hơn cho một phép tính cụ thể, với hy vọng nhận được câu trả lời nhanh hơn — nhưng chúng ta luôn có tùy chọn thực hiện phép tính tuần tự. Thật không may, việc sử dụng nhiều tài nguyên hơn không đảm bảo sẽ đưa ra câu trả lời nhanh hơn — hoặc thậm chí là chậm hơn. Và, nếu tính song song không mang lại cho chúng ta lợi nhuận (hoặc lợi nhuận âm) đối với mức tiêu thụ tài nguyên bổ sung, thì chúng ta không nên sử dụng nó. Tất nhiên, lợi nhuận ở đây phụ thuộc vào tình huống, vì vậy không có câu trả lời chung. Nhưng chúng ta có các công cụ để giúp chúng ta đánh giá xem tính song song có hiệu quả trong một tình huống nhất định hay không: phân tích, đo lường và các yêu cầu về hiệu suất.

Bài viết này chủ yếu tập trung vào phân tích — khám phá loại tính toán nào có xu hướng song song hóa tốt và loại nào không. Tuy nhiên, theo nguyên tắc thông thường, chúng ta nên sử dụng thực thi tuần tự trừ khi chúng ta có lý do để tin rằng chúng ta sẽ tăng tốc từ xử lý song song và việc tăng tốc thực sự quan trọng tùy theo yêu cầu về hiệu suất của chúng ta. (Nhiều chương trình đã đủ nhanh, vì vậy nỗ lực tối ưu hóa chúng có thể được dành cho các hoạt động tạo ra nhiều giá trị hơn, chẳng hạn như cải thiện khả năng sử dụng hoặc độ tin cậy.)

Thước đo hiệu quả song song, được gọi là speedup, chỉ đơn giản là tỷ lệ giữa thời gian chạy song song và thời gian chạy tuần tự. Chọn song song (giả sử nó mang lại khả năng tăng tốc) là một lựa chọn có chủ ý để coi trọng thời gian hơn CPU và mức sử dụng năng lượng. Quá trình thực thi song song luôn thực hiện nhiều công việc hơn so với thực thi tuần tự, vì — ngoài việc giải quyết vấn đề — nó còn phải phân tách vấn đề, tạo và quản lý các tác vụ để mô tả các bài toán con, gửi và chờ các tác vụ đó cũng như hợp nhất các kết quả của chúng.

Để sự song song trở thành sự lựa chọn tốt hơn, một số thứ phải kết hợp với nhau. Chúng ta cần một vấn đề thừa nhận một giải pháp song song ngay từ đầu - điều mà không phải vấn đề nào cũng làm được. Sau đó, chúng ta cần triển khai giải pháp khai thác tính song song vốn có. Chúng ta cần đảm bảo rằng các kỹ thuật được sử dụng để triển khai tính song song không đi kèm với quá nhiều chi phí đến mức chúng ta lãng phí các chu trình mà chúng ta dùng để xử lý vấn đề. Và chúng ta cần đủ dữ liệu để có thể đạt được quy mô kinh tế cần thiết để tăng tốc.

Khai thác Parallelism

Không phải tất cả các vấn đề đều có thể xử lý song song như nhau. Xem xét vấn đề sau: Cho một hàm f, mà chúng ta cho rằng tính toán rất tốn kém, hãy định nghĩa g như sau:

g(0) = f(0) g(n) = f( g(n‑1) ), for n > 0

chúng ta có thể thực hiện một thuật toán song song cho g và đo tốc độ của nó, nhưng chúng ta không cần phải làm vậy; chúng ta có thể nhìn vào vấn đề và thấy ngay rằng về cơ bản nó có tính tuần tự. Để thấy điều này, chúng ta có thể viết lại g(n) hơi khác một chút:

g(n) = f( f( ... n times ... f(0) ... )

Với cách viết lại này, chúng ta thấy rằng chúng ta thậm chí không thể bắt đầu tính g(n) cho đến khi chúng ta tính xong g(n-1).

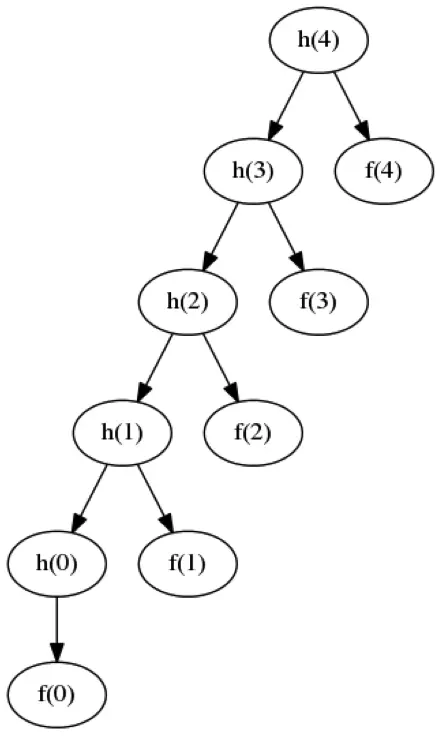
Trong sơ đồ phụ thuộc luồng dữ liệu để tính toán g(4), được hiển thị trong Hình 2, mỗi giá trị của g(n) phụ thuộc vào giá trị g(n-1) trước đó.

chúng ta có thể muốn kết luận rằng vấn đề bắt nguồn từ thực tế là g(n) được định nghĩa một cách đệ quy, nhưng thực tế không phải vậy. Xem xét bài toán tính toán hàm h(n) hơi khác một chút:

h(0) = f(0)
h(n) = f(n) + h(n‑1)

Nếu chúng ta viết triển khai rõ ràng để tính toán h(n), chúng ta sẽ có một biểu đồ phụ thuộc luồng dữ liệu giống như biểu đồ được hiển thị trong Hình 3, trong đó mỗi h(n) phụ thuộc vào h(n-1).

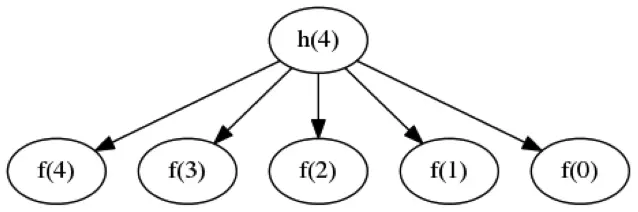
Tuy nhiên, nếu chúng ta viết lại h(n) theo một cách khác, chúng ta có thể thấy ngay vấn đề này có thể khai thác song song như thế nào. Chúng ta có thể tính toán từng điều khoản một cách độc lập và sau đó cộng chúng lại (điều này cũng thừa nhận tính song song):

h(n) = f(0) + f(1) + .. + f(n)

Kết quả là một biểu đồ phụ thuộc luồng dữ liệu giống như biểu đồ được hiển thị trong Hình 4, trong đó mỗi h(n) có thể được tính toán độc lập.

Những ví dụ này cho chúng ta thấy hai điều: thứ nhất, các vấn đề trông giống nhau có thể có mức độ song song có thể khai thác rất khác nhau; và thứ hai, việc triển khai "rõ ràng" một giải pháp cho một vấn đề với tính song song có thể khai thác có thể không nhất thiết phải khai thác tính song song đó. Để có bất kỳ cơ hội nào được tăng tốc, chúng ta cần cả hai.

Divide and conquer(Chia để trị)

Kỹ thuật tiêu chuẩn để tính song song có thể khai thác được gọi là recursive decomposition(phân rã đệ quy), hoặc divide and conquer(chia để trị). Trong cách tiếp cận này, chúng ta lặp đi lặp lại việc chia bài toán thành các bài toán con cho đến khi các bài toán con đủ nhỏ để việc giải chúng tuần tự trở nên hợp lý hơn; sau đó chúng ta giải các bài toán con song song và kết hợp các kết quả từng phần của các bài toán con để rút ra kết quả tổng.

Ví dụ 1 minh họa một giải pháp chia để trị điển hình trong pseudocode(giả mã), sử dụng CONCURRENT primitive giả định để thực thi đồng thời.

R solve(Problem<R> problem) { if (problem.isSmall()) return problem.solveSequentially(); R leftResult, rightResult; CONCURRENT { leftResult = solve(problem.leftHalf()); rightResult = solve(problem.rightHalf()); } return problem.combine(leftResult, rightResult);
}

Phân tách đệ quy hấp dẫn vì nó đơn giản (đặc biệt là khi xử lý các cấu trúc dữ liệu đã được xác định đệ quy, chẳng hạn như tree). Mã song song như trong Ví dụ 1 có thể di chuyển trên nhiều môi trường máy tính; nó hoạt động hiệu quả với một lõi hoặc nhiều lõi và nó không cần quan tâm đến sự phức tạp của việc điều phối quyền truy cập vào trạng thái có thể thay đổi được chia sẻ — bởi vì không có trạng thái có thể thay đổi được chia sẻ. Việc phân chia bài toán thành các bài toán con và sắp xếp để mỗi tác vụ chỉ truy cập dữ liệu từ một bài toán con cụ thể, thường không yêu cầu sự phối hợp giữa các luồng.

Cân nhắc về performance

Với Ví dụ 1 của chúng ta, bây giờ chúng ta có thể tiến hành phân tích các điều kiện theo đó tính song song có thể mang lại lợi thế. Hai bước thuật toán bổ sung được giới thiệu bằng phương pháp chia để trị — chia bài toán và kết hợp các kết quả từng phần — và mỗi bước trong số này có thể ít nhiều thân thiện với parallelism. Một yếu tố khác có thể ảnh hưởng đến hiệu suất song song là hiệu quả của chính các parallelism primitives — được minh họa bằng cơ chế CONCURRENT giả định trong mã giả của Ví dụ 1. Hai yếu tố bổ sung là các thuộc tính của tập dữ liệu: kích thước và vị trí bộ nhớ của nó. Chúng ta lần lượt xem xét từng điều kiện này.

Một số vấn đề, chẳng hạn như hàm g(n) trong phần " Khai thác Parallelism", hoàn toàn không có khả năng phân tách. Nhưng ngay cả khi một vấn đề có khả năng phân tách, thì việc phân tách nó có thể phải trả giá. (Ít nhất, việc phân tách một vấn đề liên quan đến việc tạo ra một mô tả về vấn đề con.) Ví dụ, bước phân tách của thuật toán Quicksort yêu cầu tìm một điểm xoay, có kích thước là O(n) của vấn đề, bởi vì nó liên quan đến kiểm tra và có thể cập nhật tất cả các dữ liệu. Yêu cầu này tốn kém hơn nhiều so với bước phân vùng của một vấn đề như "tìm tổng của một mảng các phần tử", có bước phân vùng là O(1)— "tìm giá trị trung bình của các chỉ số trên cùng và dưới cùng." Và, ngay cả khi vấn đề có thể được phân tách một cách hiệu quả, nếu hai vấn đề con có kích thước rất không bằng nhau, thì chúng ta có thể không đưa ra nhiều khả năng khai thác song song.

Tương tự, khi chúng ta giải hai bài toán con, chúng ta phải kết hợp các kết quả. Nếu vấn đề của chúng ta là "xóa các phần tử trùng lặp", thì bước kết hợp yêu cầu hợp nhất hai tập hợp; nếu chúng ta muốn biểu diễn kết quả, bước này cũng là O(n). Mặt khác, nếu vấn đề của chúng ta là "tìm tổng của một mảng", thì bước kết hợp của chúng ta lại là O(1)— "cộng hai số".

Việc quản lý các tác vụ được thực thi đồng thời có thể liên quan đến một số nguyên nhân có thể gây mất hiệu quả, chẳng hạn như độ trễ vốn có của việc chuyển giao dữ liệu từ luồng này sang luồng khác hoặc nguy cơ tranh chấp cấu trúc dữ liệu được chia sẻ.

Fork-join framework — được thêm vào trong Java SE 7 để quản lý các tác vụ chuyên sâu về tính toán, chi tiết — được thiết kế để giảm thiểu nhiều nguyên nhân phổ biến gây ra tình trạng không hiệu quả trong quá trình gửi song song. Thư viện java.util.stream sử dụng khuôn khổ fork-join để triển khai thực thi song song.

Cuối cùng, chúng ta phải xem xét dữ liệu. Nếu tập dữ liệu nhỏ, sẽ khó có thể trích xuất bất kỳ loại tăng tốc nào, do chi phí do thực thi song song gây ra. Tương tự, nếu tập dữ liệu thể hiện vị trí bộ nhớ kém (cấu trúc dữ liệu nhiều con trỏ như graphs, trái ngược với mảng), thì có khả năng là — với các hệ thống giới hạn bộ nhớ điển hình ngày nay — việc thực thi song song sẽ đơn giản dẫn đến nhiều luồng đang chờ dữ liệu từ bộ đệm, thay vì sử dụng hiệu quả các lõi để tính toán câu trả lời nhanh hơn.

Mỗi yếu tố này có thể làm giảm khả năng tăng tốc của chúng ta; trong một số trường hợp, chúng không chỉ có thể không tăng tốc độ mà thậm chí còn gây ra tình trạng chậm lại.

Định luật Amdahl

Định luật Amdahl mô tả cách phần tuần tự của phép tính giới hạn khả năng tăng tốc song song có thể xảy ra. Hầu hết các vấn đề có một số lượng công việc không thể song song; đây được gọi là serial fraction. Ví dụ: nếu chúng ta định sao chép dữ liệu từ mảng này sang mảng khác, quá trình sao chép có thể diễn ra song song, nhưng việc phân bổ mảng đích — vốn là tuần tự — phải xảy ra trước khi bất kỳ quá trình sao chép nào có thể xảy ra.

Hình 5 cho thấy tác động của luật Amdahl. Các đường cong khác nhau minh họa khả năng tăng tốc tốt nhất có thể được cho phép bởi Định luật Amdahl dưới dạng một hàm của số lượng bộ xử lý có sẵn, đối với các parallel fractions khác nhau (phần bù của serial fraction.) Ví dụ: nếu phần song song là 0.5 (một nửa bài toán phải được thực hiện tuần tự) và có vô số bộ xử lý, định luật Amdahl cho chúng ta biết rằng tốc độ tăng tốc tốt nhất mà chúng ta có thể hy vọng là gấp đôi. Điều này có thể cảm nhận được bằng trực giác; ngay cả khi chúng ta có thể giảm chi phí của phần có thể song song hóa xuống 0 thông qua song song hóa, chúng ta vẫn có một nửa vấn đề cần giải quyết tuần tự.

Hình 5. Định luật Amdahl

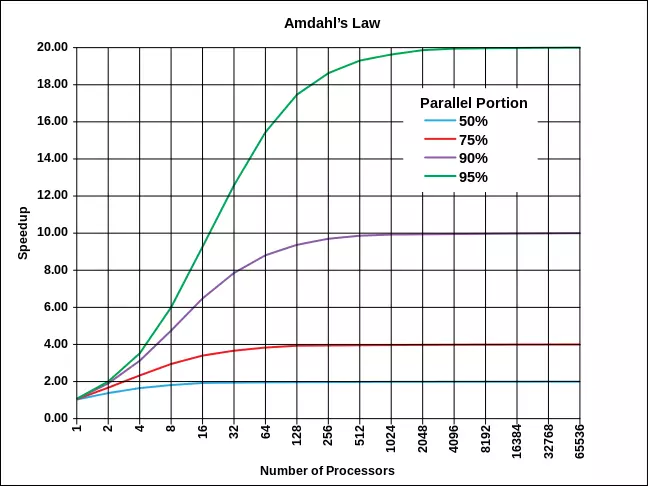
Mô hình được ngụ ý bởi Định luật Amdahl - rằng một số phần của công việc phải hoàn toàn tuần tự và phần còn lại là hoàn toàn song song. Tuy nhiên, nó vẫn hữu ích để hiểu các yếu tố ngăn cản sự song song. Khả năng phát hiện và giảm bớt serial fraction là yếu tố chính để có thể tạo ra các thuật toán song song hiệu quả hơn.

Một cách khác để diễn giải định luật Amdahl là: Nếu chúng ta có một cỗ máy 32 lõi, thì với mỗi chu trình chúng ta dành để thiết lập một phép tính song song, thì đó là 31 chu trình không thể áp dụng để giải quyết vấn đề. Và nếu chúng ta đã chia vấn đề thành hai phần, thì vẫn còn 30 chu trình sẽ bị lãng phí trên mỗi tích tắc đồng hồ. Chỉ khi chúng ta có thể phân chia đủ công việc để giữ cho tất cả các bộ xử lý bận rộn thì chúng ta mới có thể khởi động và chạy hoàn toàn — và nếu chúng ta không đến được mức đó đủ nhanh (hoặc ở đó đủ lâu), thì sẽ khó có thể tăng tốc tốt.

Kết luận cho Phần 3

Tính song song là sự đánh đổi của việc sử dụng nhiều tài nguyên điện toán hơn với hy vọng tăng tốc. Mặc dù về lý thuyết, chúng ta có thể tăng tốc một vấn đề theo hệ số N bằng cách sử dụng N lõi, nhưng thực tế thường không đạt được mục tiêu này. Các yếu tố ảnh hưởng đến hiệu quả của xử lý song song bao gồm chính vấn đề, thuật toán được sử dụng để giải quyết vấn đề, hỗ trợ thời gian chạy để phân tách và lập lịch tác vụ cũng như kích thước và vị trí bộ nhớ của tập dữ liệu.

Phần cuối của series áp dụng những cân nhắc này cho Streams library và chỉ ra cách thức (và lý do) một số stream pipelines tốt hơn những pipelines khác.