- vừa được xem lúc

[Cryptography p11] Hàm băm MD5

#Hash
#Cryptography
#Hash Functions
#MD5

0 0 3

Người đăng: Hoàng Trường Phước

Theo Viblo Asia

Bài viết được lấy từ https://truongphuoc.wordpress.com/2024/08/19/blockchain-20-4-ham-bam-md5/

Bài viết này gần 4000 chữ và gồm rất nhiều hình. Để bảo vệ đôi mắt của mình các bạn nên đọc trên máy tính nha. Vì thế nếu ai đang đọc trên điện thoại thì ghim bài này vào, sau đó đọc lại trên máy tính sau nhé.

Mở bài

Tới bài viết này chúng ta đã đi qua được hệ mật đối xứng, bất đối xứng, chữ ký điện tử và trao đổi khóa rồi, chỉ còn một mảnh ghép là hàm băm mật mã nữa là chúng ta đã hoàn thiện series rồi. Trong bài viết này chúng ta cùng đi vào chi tiết hàm băm MD5 nhé.

Ý tưởng của hàm băm trong thực tế

Trong thực tế, hàm băm giống như một máy xay sinh tố vậy, khi chúng ta cho hoa quả vào và xay, thì sẽ được sinh tố. Sinh tố là hoa quả chúng ta được băm nhỏ đến mức không thể biết hình thù quả ban đầu thế nào nữa.

Hàm băm cũng giống như một cối xay bột gạo vậy, chúng ta cho gạo vào đó, sau đó xay ra bột.

Về hàm băm cơ bản mình đã có một bài viết rồi, các bạn xem qua nhé.

Hàm băm MD5

Đơn vị tính toán trong hàm băm là bit, trong bài viết này chúng ta sẽ sử dụng cả bit dưới dạng nhị phân vào dưới dạng hex nhé.

Thông số đầu vào

MD5 nhận thông số đầu vào là bội số của 512bit, tức N*512bit (N là một số nguyên dương).

Thế dữ liệu của chúng ta không là bội số của 512bit thì sao? Ví dụ dữ liệu của chúng ta là truongphuocit với dữ liệu này thì giá trị nhị phân và hex như sau:

binary: 01110100 01110010 01110101 01101111 01101110 01100111 01110000 01101000 01110101 01101111 01100011 01101001 01110100
hex: 7472756F6E677068756F636974

Chỉ có 104bit mà thôi, không phải là bội số của 512bit, phải làm sao đây?

Đến đây chúng ta phải học kỹ thuật của những nhà làm nem chua, hoặc bánh giò, hay của các chị em gái: độn. Chúng ta sẽ độn thêm bit để được một giá trị đầu vào là bội số của 512bit. (Độn là padding trong tiếng Anh, cơ mà mình thích sử dụng tiếng Việt hơn, giàu sắc thái hơn nữa 🤣)

Kỹ thuật độn

Tất nhiên làm cái gì cũng phải có kỹ thuật mới có thể gọn mà đẹp được, việc độn cũng thế. Sau đây là kỹ thuật độn trong MD5

Kỹ thuật độn trong MD5 được gói gọn như hình trên

  • Phần đầu tiên là các bit của dữ liệu gốc
  • Phần thứ hai là một bit có giá trị là 1
  • Phần thứ ba là các bit có giá trị là 0 ở phía sau bit 1. Các bit 0 này có thể có hoặc không.
  • Phần thứ tư là 64 bit thể hiện độ dài của dữ liệu gốc. (Nếu độ dài gốc là một số lớn và 64 bit không thể hiện được thì chỉ lấy 64 bit bên phải cùng)

Chúng ta hãy cùng đi qua một số trường hợp để làm rõ vấn đề nhé, nhưng trước tiên hãy cùng nói về các con số cần chú ý:

  • 512 là số lượng bit tối đa của một khối
  • 448 = 512 - 64
  • 447 = 448 - 1

Trường hợp 1

Số bit của dữ liệu gốc nhỏ hơn 447

Lúc này chúng ta cứ theo công thức mà làm thôi, lấy ví dụ dữ liệu truongphuocit ở trên

Dữ liệu gốc:
01110100 01110010 01110101 01101111 01101110 01100111 01110000 01101000
01110101 01101111 01100011 01101001 01110100 Độ dài dữ liệu gốc là 104 bit, ta biểu diễn 104 dưới dạng số 64bit
00000000 00000000 00000000 00000000 00000000 00000000 00000000 1101000 Cuối cùng là một bit 1 đằng sau dữ liệu gốc và các bit 0 01110100 01110010 01110101 01101111 01101110 01100111 01110000 01101000
01110101 01101111 01100011 01101001 01110100 10000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 1101000

Trường hợp 2

Số bit của dữ liệu gốc bằng 447

Lúc này thì khi ta thêm 1 bit có giá trị 1 vào sau dữ liệu gốc, thì tổng số bit là 448, sau đó cộng thêm 64 thể hiện số lượng bit giá trị gốc là vừa tròn 512 bit rồi. Trong trường hợp này không có giá trị bit 0 nào được thêm vào.

Trường hợp này các bạn tự tưởng tượng làm ví dụ nha, lười viết quá mà.

Trường hợp 3

Số bit của dữ liệu gốc lớn hơn 447

Lấy một ví dụ cụ thể cho dễ hiểu: ví dụ dữ liệu của chúng ta là 448 đi, ta thêm 1 bit có giá trị 1 vào sau là 449 bit rồi, không đủ 64 bit còn lại để thể hiện giá trị độ dài dữ liệu gốc. Lúc này ta phải thêm một khối 512 bit nữa, khối này có giá trị 64 bit cuối thể hiện độ dài dữ liệu gốc, còn lại toàn 0 😆

Thông số đầu ra

Đầu ra của hàm băm md5 là một giá trị 128bit

Thuật toán

Như chúng ta đã nói ở trên, kỹ thuật băm giống như xay sinh tố hay gạo vậy, chúng ta sẽ cố gắng xáo trộn, xoay chuyển, cộng thêm... làm đủ mọi cách để dữ liệu đầu vào bị biến đổi đi. MD5 cũng thế, hãy cùng xem tổng quan về MD5 nhé.

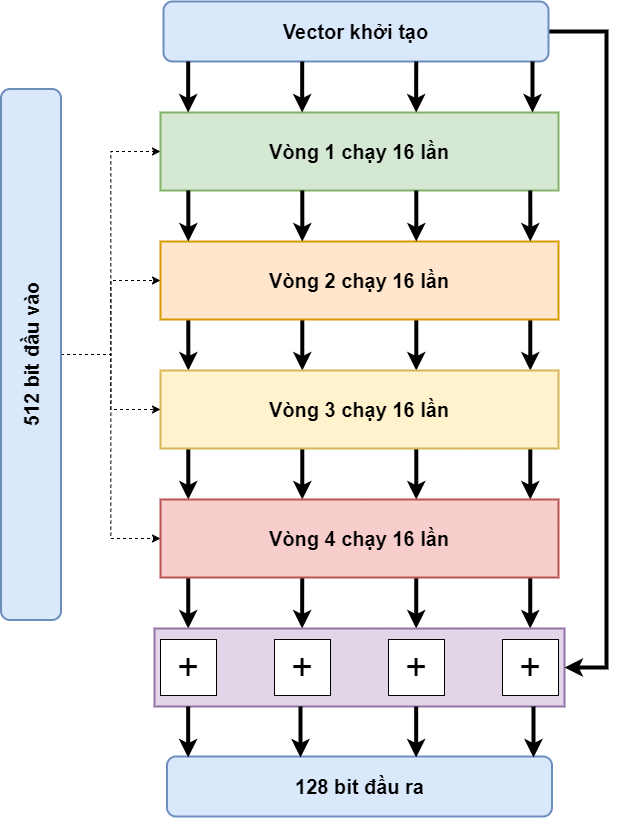
Tổng quan thuật toán như sau: Ta có một vector khởi tạo (Initialization vectors), vector này được định nghĩa trước. Từ vector này ta cho chạy qua một cái máy xay, cái máy này chạy 4 vòng (round), mỗi vòng 16 lần (operation), trong quá trình xay ta cho dữ liệu gốc vào để xay cùng. Ra được một kết quả nào đó, với kết quả này ta cộng với giá trị vector khởi tạo là ra được mã băm rồi.

Không hiểu gì phải không nào 🤣. Ta cùng đi qua từng khối một để biết chi tiết nhé.

Vector khởi tạo

Vector khởi tạo được định nghĩa sẵn gồm 4 phần, mỗi phần 32 bit được ký hiêu là A, B, C, D. Giá trị mỗi phần như sau:

A = 01234567
B = 89abcdef
C = fedcba98
D = 76543210

Xong phần vector khởi tạo.

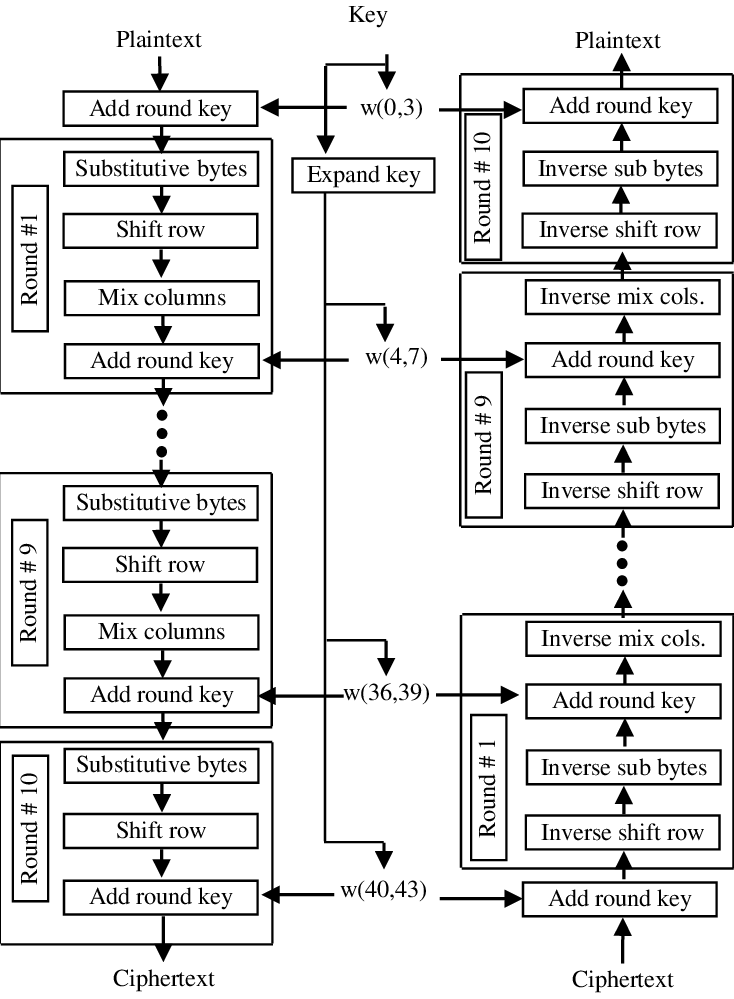
Vòng 1

Chúng ta hãy cùng soi chi tiết vòng 1 🤣 của MD5 nhé, hãy cùng xem hình dưới

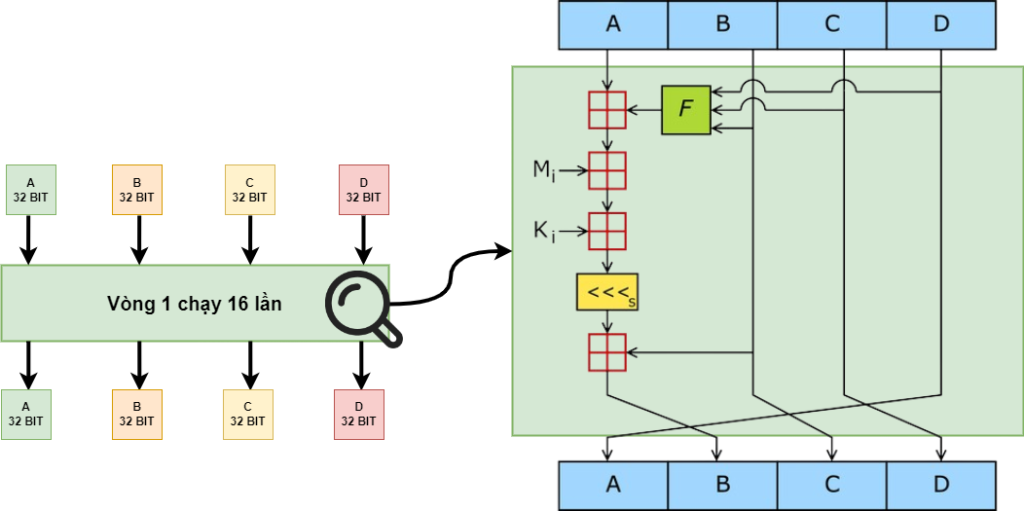
Khởi đầu với giá trị đầu vào là A, B, C và D. Đây chính là giá trị của vector khởi tạo như đã nói ở trên.

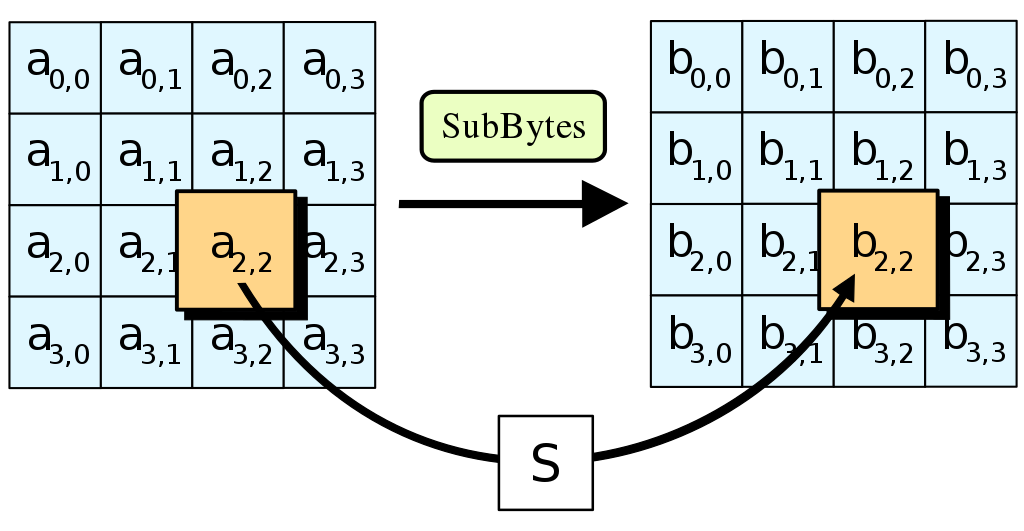
Tiếp theo là cái ô màu xanh có chữ F bên trong

Đây là đại diện cho một function F, Function này biểu diễn như sau:

F(B,C,D) = (B∧C)∨(¬B∧D)

Cái quần què gì đây😮? Xin đừng quá lo lắng sẽ có nhời giải thích sau đây

  • ∧ = AND
  • ∨ = OR
  • ¬ = NOT
  • ⊕ = XOR

Toàn những toán tử bitwise không à, nếu bạn quên đống này thì học lại nha 🤣. Với giá trị của vector khởi tạo, ta có thể tính toán như sau:

A = 01234567
B = 89abcdef
C = fedcba98
D = 76543210
F(B,C,D) = F(89abcdef,fedcba98,76543210) = (89abcdef∧fedcba98)∨(¬89abcdef∧76543210) = (89abcdef∧fedcba98)∨(¬89abcdef∧76543210) = 88888888∨(76543210∧76543210) = 88888888∨76543210 = fedcba98

Xong phần cục xanh xanh, giờ chúng ta đến với cục đo đỏ có dấu cộng cực lớn ở giữa (có 4 cục như thế trên hình)

Cục này đại diện cho phép cộng modulo 2322^{32} . Đại loại là cộng hai số với nhau, sau đó lấy tổng mod 2322^{32} đó. Tiếp tục ví dụ kết quả Function F ở phía trên và vector khởi tạo, tức cục đo đỏ đầu tiên

A = 01234567
B = 89abcdef
C = fedcba98
D = 76543210
F(B,C,D) = fedcba98
Tính:
A + F(B,C,D) mod 232
= 01234567 + fedcba98 mod 2^32
###
Tính toán theo nhị phân:
Ta chuyển hex sang dạng nhị phân
01234567 = 00000001001000110100010101100111
fedcba98 = 11111110110111001011101010011000
cộng --------------------------------
kết quả = 11111111111111111111111111111111
mod 232 = 11111111111111111111111111111111
cơ số 16 = ffffffff
###
Tính toán theo thập phân:
Trước tiên hãy tính 2^32 = 4294967296
Ta chuyển hex sang dạng thập phân
01234567 = 19088743
fedcba98 = 4275878552
cộng ----------
kết quả = 4294967295
mod 2^32 = 4294967295
cơ số 16 = ffffffff

Tại sao lại là 2322^{32} ? Ta hãy nhớ lại là trong mỗi vòng lặp các vector đầu vào A, B, C, D có 32 bit, và cũng trả về các vector đầu ra A, B, C, D có 32 bit. Sẽ như thế nào nếu phép tính cộng ra một số lớn hơn 32bit?

Ví dụ
A = ffffffff
F(B,C,D) = 00000001
Tính
A + F(B,C,D) mod 2^32
= ffffffff+ 00000001 mod 2^32
###
Tính toán theo nhị phân:
Ta chuyển hex sang dạng nhị phân
ffffffff = 11111111111111111111111111111111
00000001 = 00000000000000000000000000000001
cộng --------------------------------
kết quả= 1 00000000000000000000000000000000 (bit 1 đầu tiên là bit carry)
mod 2^32 = 00000000000000000000000000000000 (với mod 2^32 thì chỉ lấy 32 bit bên phải cùng, dẫn tới việc bỏ bit carry đi)
cơ số 16 = 00000000
###
Tính toán theo thập phân:
Trước tiên hãy tính 2^32 = 4294967296
Ta chuyển hex sang dạng thập phân
ffffffff = 4294967295
00000001 = 1
cộng ----------
kết quả = 4294967296
mod 2^32 = 0
cơ số 16 = 00000000

Bạn thấy đó, mod 2322^{32} có tác dụng chống tràn số là như vậy.

Xong cục đo đỏ đầu tiên, ta cùng đến với cục đỏ thử hai

Cục này lấy giá trị đầu vào là kết quả của cục đỏ đầu tiên và một giá trị MiM_i . Thế MiM_i là con quả nợ gì, chúng ta cùng tìm tòi tường tận nha. Chúng ta hãy quay trở lại dữ liệu gốc, nói đúng hơn là dữ liệu gốc đã được độn, có độ dài là 512bit. Chúng ta sẽ chia 512bit này thành 16 phần bằng nhau, ta ký hiện M0 -> M15, mỗi phần 32bit (12*32=512). Lấy theo ví dụ dữ liệu gốc truongphuocit ở trên ta có

Giá trị gốc đã được độn:
01110100 01110010 01110101 01101111 01101110 01100111 01110000 01101000
01110101 01101111 01100011 01101001 01110100 10000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 1101000
Chia thành 16 phần nhỏ như sau:
M0 = 01110100 01110010 01110101 01101111 = 7472756F
M1 = 01101110 01100111 01110000 01101000 = 6E677068
M2 = 01110101 01101111 01100011 01101001 = 756F6369
M3 = 01110100 10000000 00000000 00000000 = 74800000
M4 = 00000000 00000000 00000000 00000000 = 00000000
M5 = 00000000 00000000 00000000 00000000 = 00000000
M6 = 00000000 00000000 00000000 00000000 = 00000000
M7 = 00000000 00000000 00000000 00000000 = 00000000
M8 = 00000000 00000000 00000000 00000000 = 00000000
M9 = 00000000 00000000 00000000 00000000 = 00000000
M10 = 00000000 00000000 00000000 00000000 = 00000000
M11 = 00000000 00000000 00000000 00000000 = 00000000
M12 = 00000000 00000000 00000000 00000000 = 00000000
M13 = 00000000 00000000 00000000 00000000 = 00000000
M14 = 00000000 00000000 00000000 00000000 = 00000000
M15 = 00000000 00000000 00000000 1101000 = 00000068

Ở vòng thứ nhất này, với mỗi lần lặp thì MiM_i chính là M với i là số lần lặp. Ví dụ với vòng lặp đầu tiên i = 0 sử dụng M0, với vòng lặp thứ 2 thì sử dụng M1, tương tự với các vòng lặp khác. Ta có thứ tự sử dụng M như sau:

M0, M1, M2, M3, M4, M5, M6, M7, M8, M9, M10, M11, M12, M13, M14, M15

Nối tiếp ví dụ ở trên, ta có

Đặt DOT0 = A + F(B,C,D) mod 232 = 01234567 + fedcba98 mod 2^32 = ffffffff
M0 = 7472756F
DOT1 = DOT0 + M0 mod 232 = ffffffff + 7472756F mod 2^32 = 7472756E
--
Cách tính như trên, mình không viết lại nữa.

Tiếp theo tới cục đo đỏ thứ ba

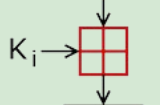
Lại một thông số KiK_i rất kỳ lạ ở đây, ta lại tiếp tục tìm để hiểu nào 😒. Giá trị của K được định nghĩa bằng công thức sau:

Ki=abs(sin(i+1))×232K_i = abs(sin(i+ 1))×2^{32}

Với i là số lần chạy từ 0->63, ta có 4 vòng mỗi vòng 16 lần chạy suy ra có 4*16 = 64 lần chạy đó. Nhìn công thức loằng ngoằng thế nên ta sẽ tính hẳn ra để làm ví dụ cho nhanh, các giá trị của K từ 0 đến 15 của vòng 1 như sau:

K0 -- D76AA478
K1 -- E8C7B756
K2 -- 242070DB
K3 -- C1BDCEEE
K4 -- F57C0FA
K5 -- 4787C62A
K6 -- A8304613
K7 -- FD469501
K8 -- 698098D8
K9 -- 8B44F7AF
K10 -- FFFF5BB1
K11 -- 895CD7BE
K12 -- 6B901122
K13 -- FD987193
K14 -- A679438E
K15 -- 49B40821

Tiếp tục với ví dụ DOT ở trên

DOT1 = 7472756E
K0 = D76AA478
DOT2 = DOT1 + K0 mod 2^32 = 7472756E + D76AA478 mod 2^32 = 4BDD19E6

Đến đây là xong cục đo đỏ thứ ba rồi, khá là mệt mỏi rồi 🫥. Cố lên chúng ta còn mấy cục nữa thôi, công thêm với 63 vòng còn lại là xong rồi 😒. Các bạn tự kéo lên xem hình tổng quan để biết đi tới đâu rồi nha, cho vào đây bài viết lại dài quá 😢

Tiếp theo đến với cục vàng vàng nào

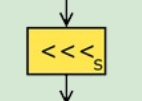
Cục này chỉ nhận một thông số đầu vào và trả ra một giá trị thôi, đây chính là phép toán xoay vòng bit sang trái nha (function ROTL), phép này xoay S bit (chữ S nho nhỏ bên dưới đó) sang trái. Lại thông số mới là S 😢. S có giá trị như sau

Với vòng 1
S0, S4, S8, S12 -- 7
S1, S5, S9, S13 -- 12
S2, S6, S10, S14 -- 17
S3, S7, S11, S15 -- 22

Tiếp nối ví dụ trước nào

DOT2 = 4BDD19E6 = 000001001011110111010001100111100110
S0 = 7 do đó dịch chuyển sang trái 7 bit
0000010 01011110111010001100111100110
<<<7
01011110111010001100111100110 0000010
ROTL = 010111101110100011001111001100000010 = 5EE8CF302

Xong cục vàng, tiếp theo tới cục đỏ cuối cùng là hết rồi, yeah. Cục này cộng ROTL với B như sau

ROTL = 5EE8CF302
B = 89abcdef
DOT3 = ROTL + B mod 2^32 = 5EE8CF302 + 89abcdef mod 2^32 = 7838C0F1

Oh yeah, xong rồi, cuối cùng sắp xếp lại để có A, B, C, D mới thôi

Giá trị ban đầu
A = 01234567
B = 89abcdef
C = fedcba98
D = 76543210
Giá trị sau
A = 76543210
B = 7838C0F1
C = 89abcdef
D = fedcba98

Giá trị A, B, C và D mới này sẽ trở thành các giá trị đầu vào cho lần chạy thứ 2, cứ như thế vòng thứ nhất chạy 16 lần.

Vòng 2

Tiếp theo cùng soi vòng 2 của MD5 xem thế nào nào 🤣

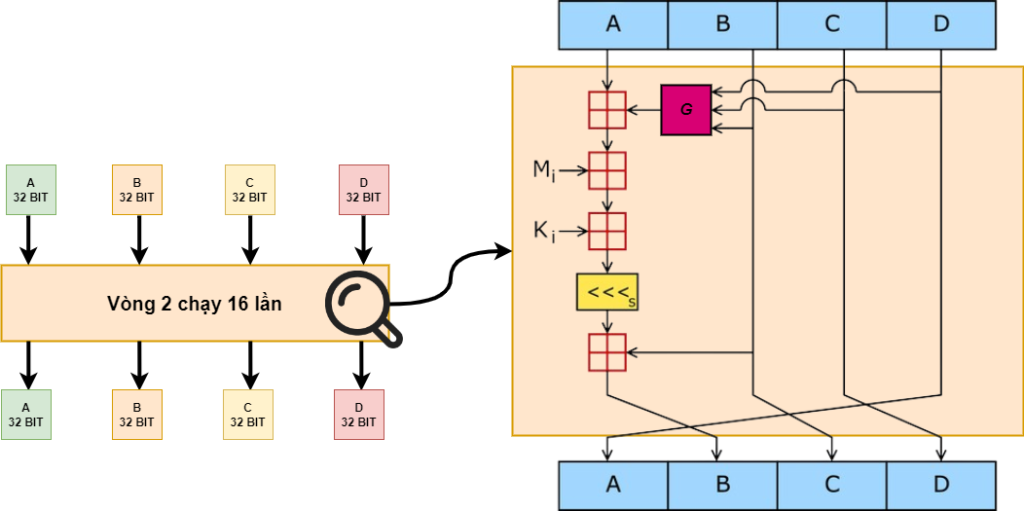
Thoạt trông vòng 2 giống hệt vòng 1. Đúng vậy, nó giống nhau lắm, chỉ khác ở một số điểm sau thôi

Đầu vào A, B, C và D của vòng 2 là kết quả A, B, C, D của vòng 1.

Hàm F được thay thế bởi hàm G, hàm G được định nghĩa như sau:

G(B, C, D) = (B∧D)∨(C∧¬D)

Nó tương tự như hàm F nhưng đổi công thức thôi nha.

Tiếp theo là MiM_i nó cũng chính là các phần của dữ liệu gốc được chia nhỏ ra như trong vòng 1, nhưng thứ tự sẽ khác đi như sau

M1, M6, M11, M0, M5, M10, M15, M4, M9, M14, M3, M8, M13, M2, M7, M12

Tiếp theo tới KiK_i, K16K_{16} đến K31K_{31} như sau

K16 -- F61E2562
K17 -- C040B340
K18 -- 265E5A51
K19 -- E9B6C7AA
K20 -- D62F105D
K21 -- 02441453
K22 -- D8A1E681
K23 -- E7D3FBC8
K24 -- 21E1CDE6
K25 -- C33707D6
K26 -- F4D50D87
K27 -- 455A14ED
K28 -- A9E3E905
K29 -- FCEFA3F8
K30 -- 676F02D9
K31 -- 8D2A4C8A

Cuối cùng là S

Với vòng 2
S16, S20, S24, S28 -- 5
S17, S21, S25, S29 -- 9
S18, S22, S26, S30 -- 14
S19, S23, S27, S31 -- 20

Vòng 2 lặp lại 16 lần với các giá trị như trên. Kết quả được các giá trị A, B, C và D. Các giá trị này lại là đầu vào của vòng 3

Vòng 3

Vòng 3 vòng 3 nào 😍

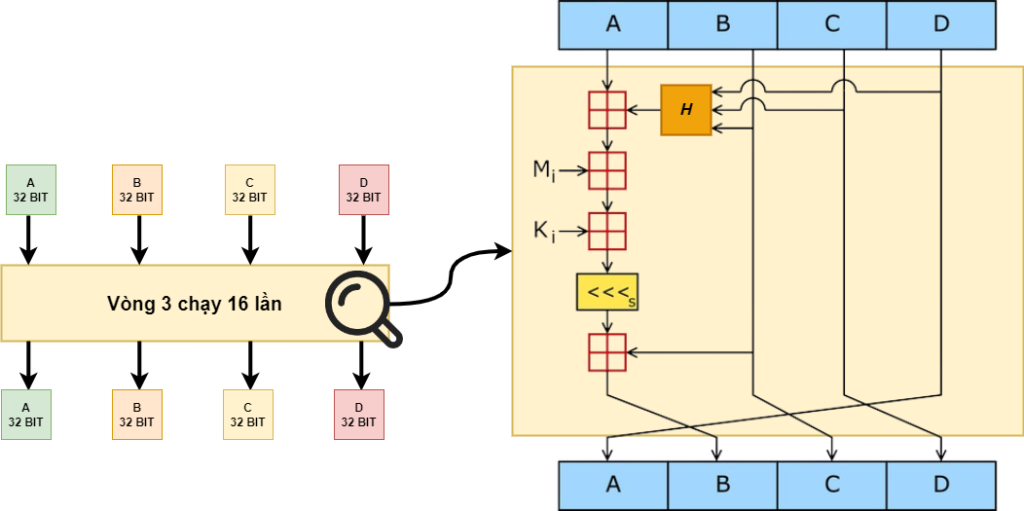
Đầu vào A, B, C và D của vòng 3 là kết quả A, B, C, D của vòng 2.

Hàm G được thay thế bởi hàm H, hàm H được định nghĩa như sau:

H(B, C, D) =B⊕C⊕D

Nó tương tự như hàm G nhưng đổi công thức thôi nha.

Tiếp theo là MiM_i nó cũng chính là các phần của dữ liệu gốc được chia nhỏ ra như trong vòng 2, nhưng thứ tự sẽ khác đi như sau

M5, M8, M11, M14, M1, M4, M7, M10, M13, M0, M3, M6, M9, M12, M15, M2

Tiếp theo tới KiK_i, K32K_{32} đến K47K_{47} như sau

K32 -- FFFA3942
K33 -- 8771F681
K34 -- 699D6122
K35 -- FDE5380C
K36 -- A4BEEA44
K37 -- 4BDECFA9
K38 -- F6BB4B60
K39 -- BEBFBC70
K40 -- 289B7EC6
K41 -- EAA127FA
K42 -- D4EF3085
K43 -- 04881D05
K44 -- D9D4D039
K45 -- E6DB99E5
K46 -- 1FA27CF8
K47 -- C4AC5665

Cuối cùng là S

Với vòng 3
S32, S36, S40, S44 -- 4
S33, S37, S41, S45 -- 11
S34, S38, S42, S46 -- 16
S35, S39, S43, S47 -- 13

Vòng 3 lặp lại 16 lần với các giá trị như trên. Kết quả được các giá trị A, B, C và D. Các giá trị này lại là đầu vào của vòng 4

Vòng 4

Cuối cùng cũng đã tới vòng 4

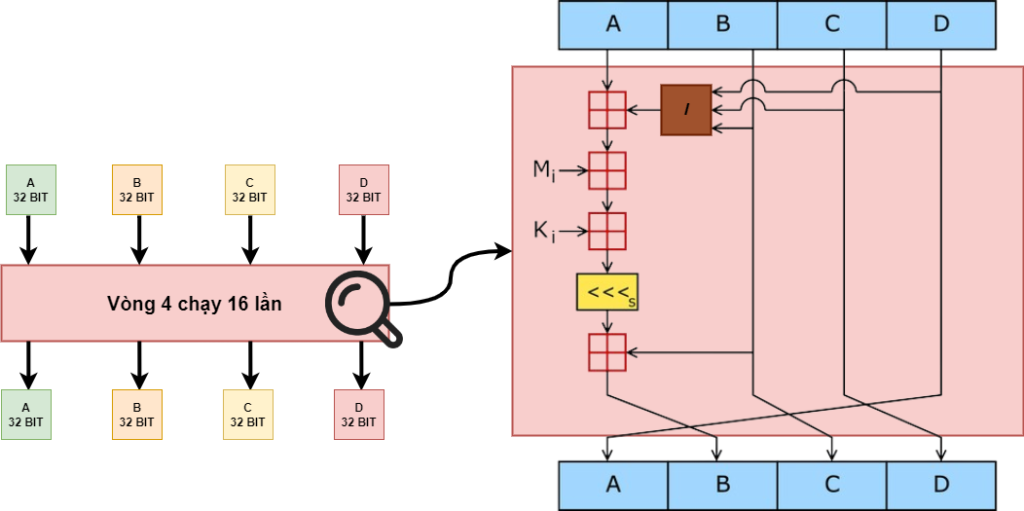
Đầu vào A, B, C và D của vòng 4 là kết quả A, B, C, D của vòng 3.

Hàm H được thay thế bởi hàm I, hàm I được định nghĩa như sau:

I(B, C, D) = C⊕(B∨¬D)

Nó tương tự như hàm H nhưng đổi công thức thôi nha.

Tiếp theo là MiM_i nó cũng chính là các phần của dữ liệu gốc được chia nhỏ ra như trong vòng 3, nhưng thứ tự sẽ khác đi như sau

M0, M7, M14, M5, M12, M3, M10, M1, M8, M15, M6, M13, M4, M11, M2, M9

Tiếp theo tới KiK_i, K48K_{48} đến K63K_{63} như sau

K48 -- F4292244
K49 -- 432AFF97
K50 -- AB9423A7
K51 -- FC93A039
K52 -- 655B59C3
K53 -- 8F0CCC92
K54 -- FFEFF47D
K55 -- 85845DD1
K56 -- 6FA87E4F
K57 -- FE2CE6E0
K58 -- A3014314
K59 -- 4E0811A1
K60 -- F7537E82
K61 -- BD3AF235
K62 -- 2AD7D2BB
K63 -- EB86D391

Cuối cùng là S

Với vòng 4
S48, S52, S56, S60 -- 6
S49, S53, S57, S61 -- 10
S50, S54, S58, S62 -- 15
S51, S55, S59, S63 -- 21

Vòng 4 lặp lại 16 lần với các giá trị như trên. Kết quả được các giá trị A, B, C và D. Các giá trị này lại là đầu vào của phép tính cộng tiếp theo.

Cộng với vector khởi tạo

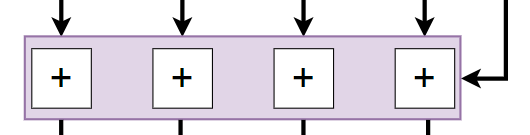
Sau khi chạy xong cả 4 vòng ta được kết quả là các giá trị A, B, C và D. Bước tiếp theo ta sẽ cộng modulo 2322^{32} các giá trị trên với vector khởi tạo.

Phép cộng modulo 2322^{32} đã biểu diễn ở trên rồi, chỉ cần cộng giá trị đầu ra với hàm khởi tạo là xong

A mới = (A kết quả của vòng 4 + vector A khởi tạo) mod 232
B mới = (B kết quả của vòng 4 + vector B khởi tạo) mod 232
C mới = (C kết quả của vòng 4 + vector C khởi tạo) mod 232
D mới = (D kết quả của vòng 4 + vector D khởi tạo) mod 232

Phần này các bạn tự tưởng tượng làm ví dụ nha, mình đuối quá rồi 👌

"Nối vòng tay lớn"

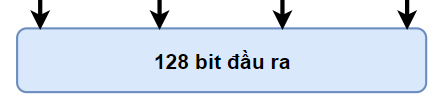
Cuối cùng nối A, B, C, D vào với nhau để ra mã băm nào

Hash = ABCD
Ví dụ
A = a9cbc8ef
B = 12cb3fe9
C = 73c5cee3
D = e1ccb4ea
Hash = ABCD = a9cbc8ef12cb3fe973c5cee3e1ccb4ea

Ta thấy rằng mỗi giá trị A, B, C, D có độ dài là 32 bit, do đó Hash có độ dài 32*4=128 bit

Nếu đầu vào có giá trị lớn hơn 512bit

Nếu thế thì ta sẽ chạy thêm thôi, xem hình dưới là hiểu ngay

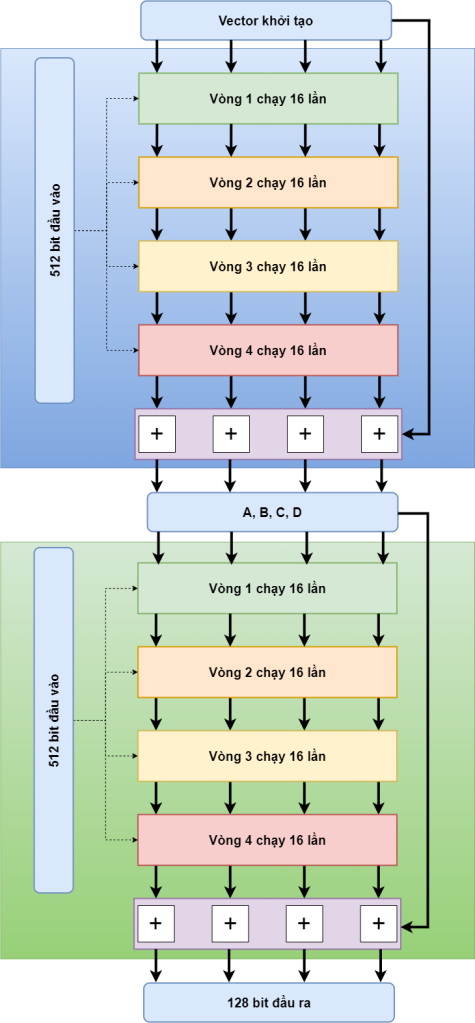
Có bao nhiêu thì ta chạy bấy nhiêu thôi, sợ gì nào 😊

Các lỗ hổng bảo mật của MD5

Collision vulnerabilities

Collision vulnerabilities hay gọi là lỗ hổng va chạm, đây là trường hợp khi hai giá trị đầu vào khác nhau trả về cùng một giá trị băm. Ví dụ

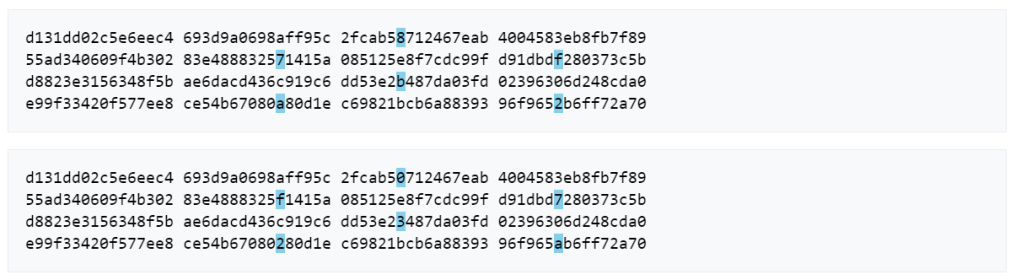
Đều trả về giá trị băm là 79054025255fb1a26e4bc422aef54eb4 . Tham khảo thêm tại wikipedia

Preimage Attack

Preimage Attack hay tấn công tiền ảnh là nhằm tìm một thông điệp mà khi băm, sẽ tạo ra giá trị băm đã cho trước.

Giả sử ta có một giá trị băm MD5 là d41d8cd98f00b204e9800998ecf8427e, đây là giá trị băm của chuỗi rỗng (""). Một cuộc tấn công tiền ảnh sẽ cố gắng tìm một chuỗi dữ liệu khác với chuỗi rỗng nhưng vẫn tạo ra cùng một giá trị băm này. Tham khỏa thêm tại đây và đây

Kết luận

Đến đây chúng ta đã tìm hiểu xong về hàm băm MD5, quả là dài phải không nào. Các bạn thấy đó, MD5 cộng, dịch chuyển bit, rồi đi qua function các kiểu, phải chạy tới tám tám sáu tư lần mà vẫn có những lỗ hổng bảo mật 🤣. Hiện nay người ta khuyến nghị không nên sử dụng MD5 nữa rồi. Tiếp theo chúng ta sẽ đi tới một họ thuật toán băm cao cấp hơn họ MD, là họ SHA nha.

Tài liệu tham khảo và công cụ

  1. https://en.wikipedia.org/wiki/MD5
  2. https://www.comparitech.com/blog/information-security/md5-algorithm-with-examples/
  3. https://www.binaryhexconverter.com/binary-to-hex-converter
  4. https://en.wikipedia.org/wiki/Preimage_attack
  5. https://www.rapidtables.com/convert/number/hex-to-binary.html?x=4BDD19E6

Link bài viết gốc https://truongphuoc.wordpress.com/2024/08/19/blockchain-20-4-ham-bam-md5/

Bình luận

Bài viết tương tự

- vừa được xem lúc

Giới thiệu về Hash trong Ruby và Rails

. Hash là một cấu trúc dữ liệu lưu trữ bằng các khóa liên quan. Điều này trái ngược với array lưu trữ các mục theo một chỉ mục có thứ tự.

0 0 36

- vừa được xem lúc

Phần 3: Tự tạo ra một đồng tiền ảo Bitcoin của mình

Trending

Tiền ảo là gì. Lúc này thì khái niệm TIỀN ẢO mới ra đời.

0 0 53

- vừa được xem lúc

Data structures: Hash table

Giới thiệu. Hash Table là một cấu trúc dữ liệu vô cùng quan trọng có ở hầu hết các ngôn ngữ, là một tronng nhữg nền tảng của Cấu trúc dữ liệu và thuật toán.

0 0 32

- vừa được xem lúc

[Cryptography p12] Hàm băm SHA256

Bài viết được lấy từ https://truongphuoc.wordpress.com/2024/08/22/blockchain-20-5-ham-bam-sha256/. Bài này này gồm gần 3000 chữ và rất nhiều hình ảnh, công thức.

0 0 4

- vừa được xem lúc

Mật mã học: Phần 1 - Mã hóa Caesar

Trending

Khái niệm mã hóa dữ liệu và giải mã. Mã hóa dữ liệu là tiến trình che dấu dữ liệu thật (plaintext), nghĩa là chuyển dữ liệu thật thành dữ liệu không có ý nghĩa hoặc có ý nghĩa khác xa với dữ liệu thật

0 0 50

- vừa được xem lúc

Thực hành mã hóa và giải mã thuật toán Simplified AES

Tương tự bài viết trước về thuật toán Simplified DES, mình sẽ không thảo luận về lý thuyết của tiêu chuẩn mã hóa dữ liệu Advanced Encryption Standard - AES, hay cụ thể là Simplified AES. Thay vào đó,

0 0 168