Bài viết được lấy từ https://truongphuoc.wordpress.com/2024/08/22/blockchain-20-5-ham-bam-sha256/

Bài này này gồm gần 3000 chữ và rất nhiều hình ảnh, công thức. Các bạn nên đọc trên máy tính để bảo vệ đôi mắt và bộ não của mình nha 🤣

Lời dẫn

Họ hàm băm SHA, đặc biệt SHA2 ngày nay được sử dụng rộng rãi trong cuộc sống. Hôm nay chúng ta sẽ tìm hiểu một hàm băm trong họ SHA2 là SHA256 nhé.

Bài viết này không phải độc lập, mình sử dụng những kiến thức của bài trước MD5. Nếu ai chưa đọc bài đó thì có thể tham khảo, để có thể đọc bài viết này dễ dàng hơn nhé 👌

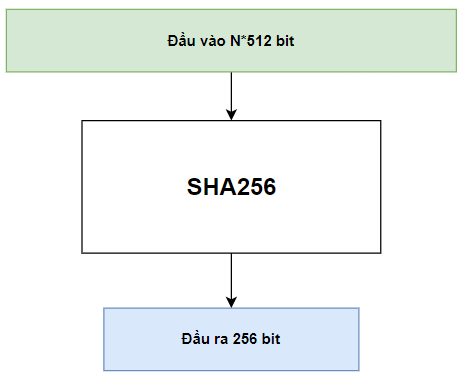
Đầu vào

SHA256 có đầu vào là 512bit, và cách padding giống như của MD5, trong bài trước mình có viết rồi nên bài này mình không viết lại nha, lười lắm.

Đọc thêm hàm băm MD5

Đầu ra

SHA256 giống như tên gọi của nó, đầu ra là 256 bit

Thuật toán băm

Hàm băm giống như một cái máy xay vậy, nó xoay liên tục, rồi thêm, rồi đảo, rồi cắt bớt,... Làm đủ mọi cách để dữ liệu biến đổi, mất đi định dạng ban đầu. Cùng xem "chiếc máy xay" SHA256 hoạt động thế nào nhé

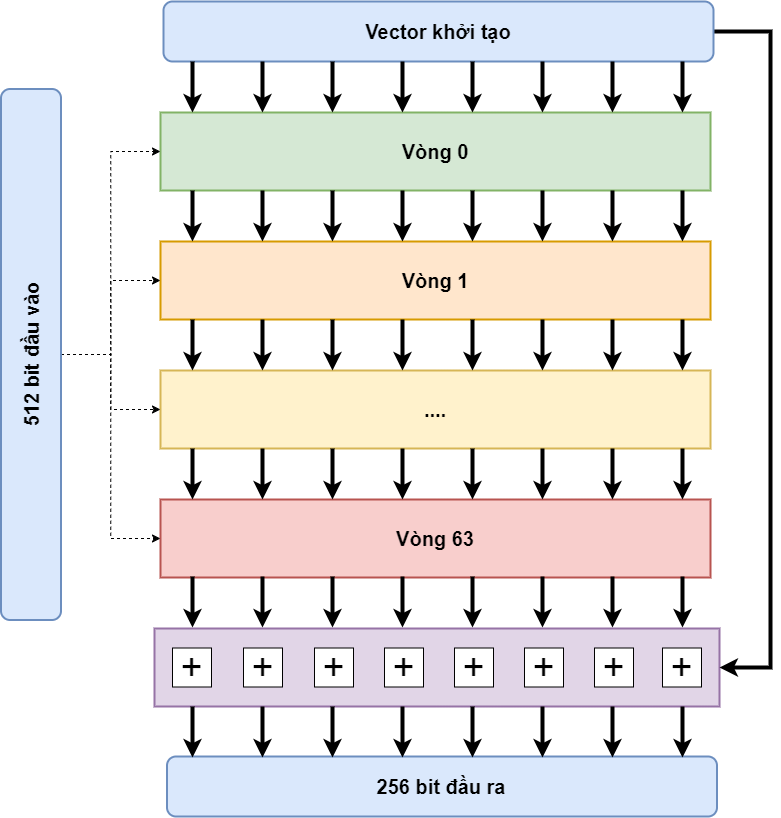
Thoạt trông SHA256 cũng na ná giống với MD5 phải không nào, chỉ khác là giờ không chia thành 4 vòng, mỗi vòng chạy 16 lần nữa là chia hẳn thành 64 vòng luôn rồi.

Hãy tìm hiểu từng cục một trong hình trên nhé.

Vector khởi tạo

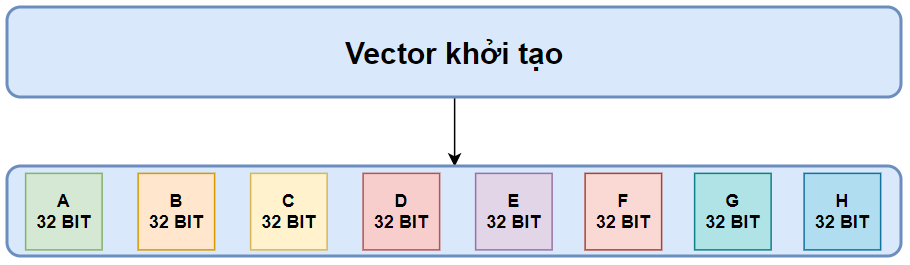
Vector khởi tạo của SHA256 được định nghĩa là có 8 phần, gọi là A, B, C, D, E, F, G, H. Giá trị của các phần như sau

A = 01101010000010011110011001100111 = 6a09e667
B = 10111011011001111010111010000101 = bb67ae85
C = 00111100011011101111001101110010 = 3c6ef372
D = 10100101010011111111010100111010 = a54ff53a
E = 01010001000011100101001001111111 = 510e527f
F = 10011011000001010110100010001100 = 9b05688c
G = 00011111100000111101100110101011 = 1f83d9ab
H = 01011011111000001100110100011001 = 5be0cd19

Xong phần vector khởi tạo

Chi tiết một vòng

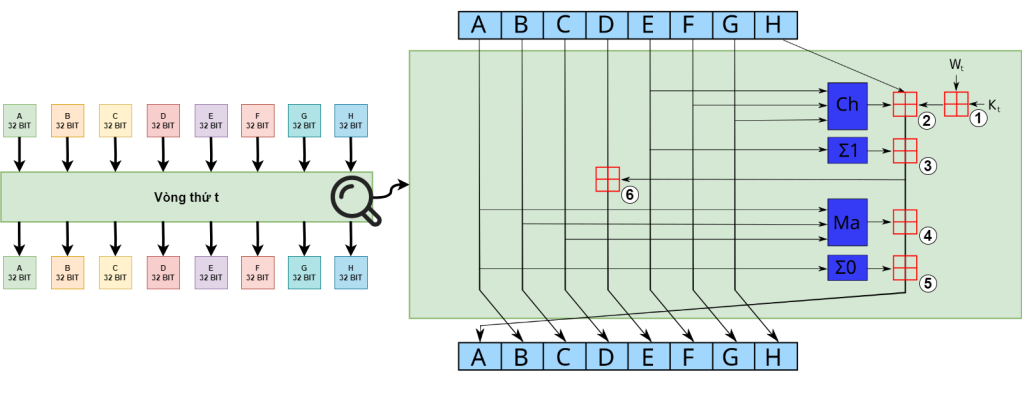
Cùng điểm qua các ký hiệu, các cục trên hình một chút nha.

Hình trên đại diện cho một vòng t, có các phép toán cộng modulo 2^32 giống như ở MD5 là cục vuông có dấu cộng màu đỏ to đùng ở giữa á, mình có đánh số từ 1 đến 6 để mọi người tiện theo dõi.

Có các function là Ch, Σ1, Ma, Σ0 màu xanh nước biển như hình. Còn có $W_t$ và $K_t$ ở bên phải trên cùng các bạn có thể nhìn thấy.

Chúng ta cùng tìm hiểu $W_t$ và $K_t$ trước nha.

$W_t$

Để tính toán được $W_t$ ta phải quay lại với dữ liệu gốc, ý mình muốn nói là dữ liệu gốc đã được độn để có độ dài 512bit bit nha. Ta chia dữ liệu gốc này thì 16 phần bằng nhau, mỗi phần 32 bit (12*32 = 512). Cách chia giống với MD5, cùng lấy lại ví dụ với dữ liệu gốc là truongphuocit trong bài MD5 nha

Giá trị gốc đã được độn:
01110100 01110010 01110101 01101111 01101110 01100111 01110000 01101000
01110101 01101111 01100011 01101001 01110100 10000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 1101000
Chia thành 16 phần nhỏ như sau:
M0 = 01110100 01110010 01110101 01101111 = 7472756F
M1 = 01101110 01100111 01110000 01101000 = 6E677068
M2 = 01110101 01101111 01100011 01101001 = 756F6369
M3 = 01110100 10000000 00000000 00000000 = 74800000
M4 = 00000000 00000000 00000000 00000000 = 00000000
M5 = 00000000 00000000 00000000 00000000 = 00000000
M6 = 00000000 00000000 00000000 00000000 = 00000000
M7 = 00000000 00000000 00000000 00000000 = 00000000
M8 = 00000000 00000000 00000000 00000000 = 00000000
M9 = 00000000 00000000 00000000 00000000 = 00000000
M10 = 00000000 00000000 00000000 00000000 = 00000000
M11 = 00000000 00000000 00000000 00000000 = 00000000
M12 = 00000000 00000000 00000000 00000000 = 00000000
M13 = 00000000 00000000 00000000 00000000 = 00000000
M14 = 00000000 00000000 00000000 00000000 = 00000000
M15 = 00000000 00000000 00000000 1101000 = 00000068

Công thức tính $W_t$

Với $W_0$ tới $W_{15}$ , ta lấy theo đúng M0 tới M15. Tức $W_0$ = M0, $W_1$ = M1 tương tự như thế

Với $W_{16}$ trở đi, ta tính theo công thức sau:

$W_t = σ_1 (W_{t-2}) + W_{t-7} + σ_1 (W_{t-15}) + W_{t-16}$

Cái quần què gì ở trên thế 😮??? Các bạn hãy bình tĩnh, giữ một đôi chân nóng và một cái đầu lạnh nha. Chúng ta cùng đi vào từng thành phần một

Đầu tiên là con của nợ σ này, nó là ký hiệu của sigma nha. Công thức của nó như sau:

$σ_1(x) = ROTR^{17}(x)⊕ROTR^{19}(x)⊕SHR^{10}(x)$

$σ_0(x) = ROTR^7(x)⊕ROTR^{18}(x)⊕SHR^3(x)$

Với hai công thức trên ta có thấy có các function là ROTR và SHR , đồng thời có toán tử ⊕ (toán tử XOR). Để tính được $σ_1$ và $σ_0$ ta phải tìm hiểu hai function ROTR và SHR

ROTR

Đây là function viết tắt của Rotate Right, có nghĩa là xoay sang phải, với số lần xoay được đánh dấu ở phía trên. Lấy một ví dụ cho các bạn dễ hiểu nha

M0 = 01110100 01110010 01110101 01101111 = 7472756F
ROTR17 (W0) = ROTR17 (7472756F) = ROTR17 (01110100 01110010 01110101 01101111) = 00111010 10110111 10111010 00111001 = 3AB7BA39

Trên là ví dụ xoay 17 bit sang phải.

SHR

Đây là function viết tắt của Shift Right tức là phép dịch phải, với phép dịch này thì dữ liệu sẽ không xoay về bên trái mà sẽ mất đi. Số lần dịch được đánh đấu ở phía trên. Bao nhiêu lời nói không bằng một ví dụ, cùng lấy ví dụ nào

M0 = 01110100 01110010 01110101 01101111 = 7472756F
SHR10 (W0) = SHR10 (7472756F) = SHR10 (01110100 01110010 01110101 01101111) = 00000000 00011101 00011100 10011101 = 001D1C9D
// Đã dịch chuyển 10bit sang bên phải
// Các bit thiếu bên trái được thay thế bằng bit 0

Ở trên là ví dụ dịch chuyển 10bit sang phải.

Sự khác biệt giữa ROTR và SHR:

ROTR không làm mất mát dữ liệu, dữ liệu chỉ bị xáo trộn mà thôi
SHR làm mất mát dữ liệu.

XOR (⊕ )

Phép XOR này mình không viết lại đâu, chỉ liệt kê ra cho đẹp thôi. Hì hì 🤣

Phép cộng modulo (+)

Cuối cùng là phép cộng. Đây là phép công modulo $2^{32}$ . Mình đã giải thích ở bài Hàm băm MD rồi, cũng không viết lại đâu, lười lắm rồi.

Ví dụ

Cuối cùng, ráp lại với nhau, là ra được kết quả rồi. Hãy cùng đến với ví dụ về $W_{16}$ nhé. Tool đây

$W16 = σ_1 (W_{16-2}) + W_{16-7} + σ_0 (W_{16-15}) + W_{16-16} = σ_1 (W_{14}) + W_9 + σ_0 (W_1) + W_0$

Tất cả các giá trị bên dưới đều viết dưới cơ số 16 (hex)
---------
Viết lại công thức
σ1(x) = ROTR17(x)⊕ROTR19(x)⊕SHR10(x)
σ0(x) = ROTR7(x)⊕ROTR18(x)⊕SHR3(x)
W16 = σ1 (W14) + W9 + σ0 (W1) + W0
Tính toán
σ1(W14) = σ1(00000000) = ROTR17(00000000)⊕ROTR19(00000000)⊕SHR10(00000000) = 00000000
σ0(W1) = σ0(6E677068) = ROTR7(6E677068)⊕ROTR18(6E677068)⊕SHR3(6E677068) = D0DCCEE0⊕DC1A1B99⊕DCCEE0D = 010A3B74
W16 = σ1 (W14) + W9 + σ0 (W1) + W0 = 00000000 + 00000000 + 010A3B74+ 7472756F = 757CB0E3

Các giá trị khác từ $W_{17}$ tới $W_{63}$ tính tương tự nha.

Quay lại tiếp nào, đến đây quên luôn ban đầu làm gì rồi. À đang tìm hiểu các thông số $W_t$ và $K_t$ không nhớ thì chịu khó cuộn lên xem lại nha. Ta đã tính được $W_t$ rồi, tiếp theo là $K_t$ nào

$K_t$

Thật may mắn cho chúng ta là $K_t$ được định nghĩa sẵn như sau

K0 = 428A2F98 K16 = E49B69C1 K32 = 27B70A85 K48 = 19A4C116
K1 = 71374491 K17 = EFBE4786 K33 = 2E1B2138 K49 = 1E376C08
K2 = B5C0FBCF K18 = 0FC19DC6 K34 = 4D2C6DFC K50 = 2748774C
K3 = E9B5DBA5 K19 = 240CA1CC K35 = 53380D13 K51 = 34B0BCB5
K4 = 3956C25B K20 = 2DE92C6F K36 = 650A7354 K52 = 391C0CB3
K5 = 59F111F1 K21 = 4A7484AA K37 = 766A0ABB K53 = 4ED8AA4A
K6 = 923F82A4 K22 = 5CB0A9DC K38 = 81C2C92E K54 = 5B9CCA4F
K7 = AB1C5ED5 K23 = 76F988DA K39 = 92722C85 K55 = 682E6FF3
K8 = D807AA98 K24 = 983E5152 K40 = A2BFE8A1 K56 = 748F82EE
K9 = 12835B01 K25 = A831C66D K41 = A81A664B K57 = 78A5636F
K10 = 243185BE K26 = B00327C8 K42 = C24B8B70 K58 = 84C87814
K11 = 550C7DC3 K27 = BF597FC7 K43 = C76C51A3 K59 = 8CC70208
K12 = 72BE5D74 K28 = C6E00BF3 K44 = D192E819 K60 = 90BEFFFA
K13 = 80DEB1FE K29 = D5A79147 K45 = D6990624 K61 = A4506CEB
K14 = 9BDC06A7 K30 = 06CA6351 K46 = F40E3585 K62 = BEF9A3F7
K15 = C19BF174 K31 = 14292967 K47 = 106AA070 K63 = C67178F2

Thế là đã xong phần các thông số, ta cùng làm ví dụ vòng thứ 0 để vừa đi qua từng function một vừa có ví dụ luôn nha.

Vòng 0

Ta sẽ đi qua từng phép cộng được đánh số

Phép cộng thứ nhất

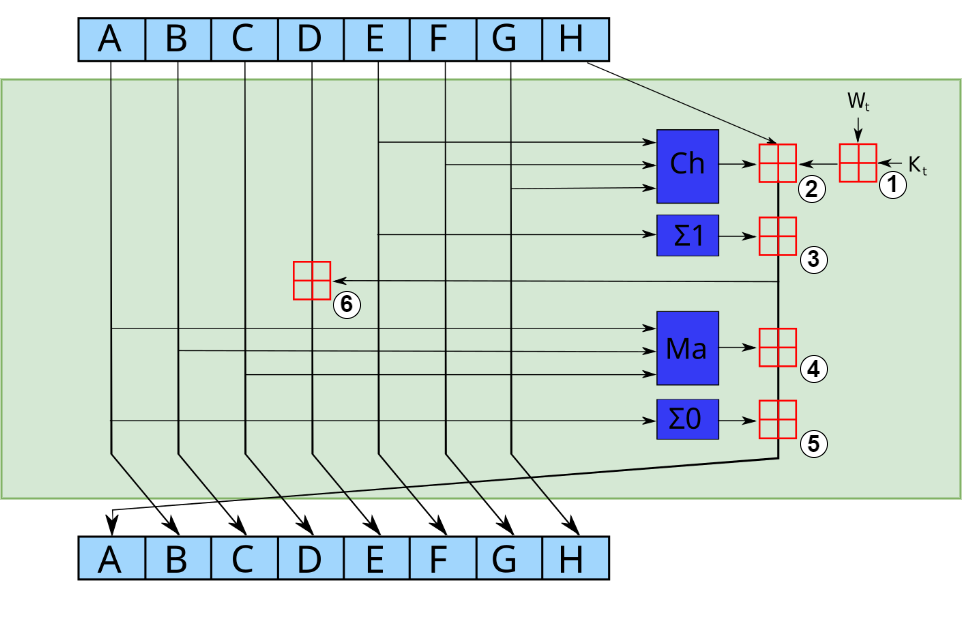
Phép cộng của $W_t$ và $K_t$ với t = 0

W0 = 7472756F
K0 = 428A2F98
DOT1 = W0 + K0 mod 2^32 = 7472756F + 428A2F98 mod 2^32 = B6FCA507
// Cách tính đã nói rõ ràng trong bài MD5 nên không viết lại nha

Phép cộng thứ hai

Phép cộng thứ hai là tổng của ba tham số

Kết quả phép cộng thứ nhất: DOT1
Giá trị của H
Kết quả của function Ch

Tới đây ta đã có DOT1 và H rồi, giờ còn tính Ch nữa thôi.

function CH

Function Ch được định nghĩa như sau:

Ch(E,F,G)=(E∧F)⊕(¬E∧G)

Các toán tử trên là toán tử bitwise, mình đã nói ở bài MD5 rồi, giờ xin viết lại ở đây để dễ nhớ nha

∧ = AND
∨ = OR
¬ = NOT
⊕ = XOR

Đấy, ai mà không biết tính thế nào thì lên ông Google hỏi nha 🤣👌. Cùng làm tiếp nào

E = 510e527f
F = 9b05688c
G = 1f83d9ab
Ch(E,F,G) = (E∧F)⊕(¬E∧G) = (510e527f∧9b05688c)⊕(¬510e527f∧1f83d9ab) = 1104400c⊕(AEF1AD80∧1f83d9ab) = 1104400c⊕0e818980 = 1f85c98c

Thế là có giá trị của Ch rồi, giờ tính tiếp DOT2 nào

DOT2 = DOT1 + H + Ch(E,F,G) mod 2^32 = B6FCA507 + 5be0cd19 + 1f85c98c mod 2^32 = 32633BAC

Phép cộng thứ ba

Phép cộng thứ ba là tổng của DOT2 và function Σ1 với Σ1 được định nghĩa như sau

FUNCTION Σ1

$Σ1(E) = ROTR^6(E)⊕ROTR^{11}(E)⊕ROTR^{25}(E)$

Ta cùng đến với ví dụ, các bạn có thể sử dụng tool này để tính nhé

Σ1(E) = ROTR6(E)⊕ROTR11(E)⊕ROTR25(E)
Σ1(510e527f) = ROTR6(510e527f)⊕ROTR11(510e527f)⊕ROTR25(510e527f) = FD443949⊕4FEA21CA⊕87293FA8 = b2ae1883⊕87293FA8 = 3587272B

Đã có kết quả Σ1 ta cộng với DOT2 như sau

DOT3 = DOT2 + Σ1 mod 2^32 = 32633BAC + 3587272b mod 2^32 = 67EA62D7

Phép cộng thứ tư

Đây là phép cộng của DOT3 với kết quả của một function Ma (quá mệt mỏi, quá nhiều phép cộng, quá nhiều function 😢) function Ma được định nghĩa như sau

FUNCTION MA

$Ma(A,B,C) = (A∧B)⊕(A∧C)⊕(B∧C)$

Toàn các phép toán đơn giản ha, hãy tiếp tục ví dụ nào

A = 6a09e667
B = bb67ae85
C = 3c6ef372
Ma(A,B,C) = (A∧B)⊕(A∧C)⊕(B∧C) = (6a09e667∧bb67ae85)⊕(6a09e667∧3c6ef372)⊕(bb67ae85∧3c6ef372) = 2A01A605⊕2808E262⊕3866A200 = 02094467⊕3866A200 = 3A6FE667

Tính tiếp DOT4

DOT4 = DOT3 + Ma(A,B,C) mod 2^32 = 67EA62D7 + 3A6FE667 mod 2^32 = A25A493E

Phép cộng thứ năm

Phép cộng thứ năm là phép cộng DOT4 với kết quả của funcion Σ0 (tiếp function tiếp 😒).

FUCTION Σ0

Σ0 như sau

$Σ0(A) = ROTR^2(A)⊕ROTR^{13}(A)⊕ROTR^{22}(A)$

Giống Σ1 phải không nào, khác mỗi thông số thôi, cùng tính toán nhé

A = 6a09e667
Σ0(A) = ROTR2(A)⊕ROTR13(A)⊕ROTR22(A) = ROTR2(6a09e667)⊕ROTR13(6a09e667)⊕ROTR22(6a09e667) = DA827999⊕333B504F⊕27999DA8 = e9b929d6⊕27999DA8 = CE20B47E

Đã có Σ0 rồi thì tiếp tới DOT5 nào

DOT5 = DOT4 + Σ0 = A25A493E + CE20B47E mod 2^32 = 707AFDBC

Phép cộng thứ sáu

Con này là cộng giữa DOT3 và D, cùng tính thôi

DOT6 = DOT3 + D mod 2^32 = 67EA62D7 + a54ff53a mod 2^32 = 0D3A5811

Tổng hợp kết quả

Cuối cùng ta tổng hợp lại để ra được vector đã biến đổi nhé

A0 = DOT5 = 707AFDBC
B0 = A = 6a09e667
C0 = B = bb67ae85
D0 = C = 3c6ef372
E0 = DOT6 = 0D3A5811
F0 = E = 510e527f
G0 = F = 9b05688c
H0 = G = 5be0cd19

Các vòng còn lại

Vòng tiếp theo là vòng 1 sẽ nhận kết quả đầu ra của vòng 0 (là các số A0, B0,... ở trên đó) làm đầu vào.

Vòng 2 sẽ nhận kết quả đầu ra của vòng 1 làm đầu vào, cứ tiếp diễn như thế đến vòng 63.

Cách tính toán mỗi vòng giống nhau, chỉ khác thông số đã nói ở trên rồi nha.

Đến đây là hết các vòng rồi, chuyển qua hình tổng quan ở trên cùng nha.

Cộng cuối

Tiếp theo là phần cộng này, giống như trong MD5 thôi, ta cộng kết quả đầu ra của vòng 63 với vector khởi tạo.

Ví dụ kết quả đầu ra của vòng 63 là

A63 = 05F5E100
B63 = 07270E00
C63 = 0754D4C0
D63 = 0D50D040
E63 = 1A7DAF1C
F63 = 0E91ED1C
G63 = 13447061
H63 = 1399BFD7

Bạn nhớ vector khởi tạo chứ, không nhớ thì roll lên đọc lại nha 🤣

Cộng nào

Tất cả phép cộng dưới đây là phép cộng modulo 2^32
A' = A + A63 = 6a09e667 + 05F5E100 = 6FFFC767
B' = B + B63 = bb67ae85 + 07270E00 = C28EBC85
C' = C + C63 = 3c6ef372 + 0754D4C0 = 43C3C832
D' = D + D63 = a54ff53a + 0D50D040 = B2A0C57A
E' = E + E63 = 510e527f + 1A7DAF1C = 6B8C019B
F' = F + F63 = 9b05688c + 0E91ED1C = A99755A8
G' = G + G63 = 1f83d9ab + 13447061 = 32C84A0C
H' = H + H63 = 5be0cd19 + 1399BFD7 = 6F7A8CF0

'Nối vòng tay lớn'

Cuối cùng nối kết quả vào với nhau để ra mã hash nào

Hash = A'B'C'D'E'F'G'H' = 6FFFC767C28EBC8543C3C832B2A0C57A6B8C019BA99755A832C84A0C6F7A8CF0

Ta có 8 phần, mỗi phần 32 bit, nên tổng là 32*8=256 bit đầu ra, vừa đẹp.

Đầu vào là N*512 với N>1

Nếu đầu vào có nhiều hơn một khối 512bit thì sao? Ví dụ có 2, 3 khối, ta phải làm thế nào? Lúc này ta tính tiếp thôi, xem hình bên dưới là hiểu ngay

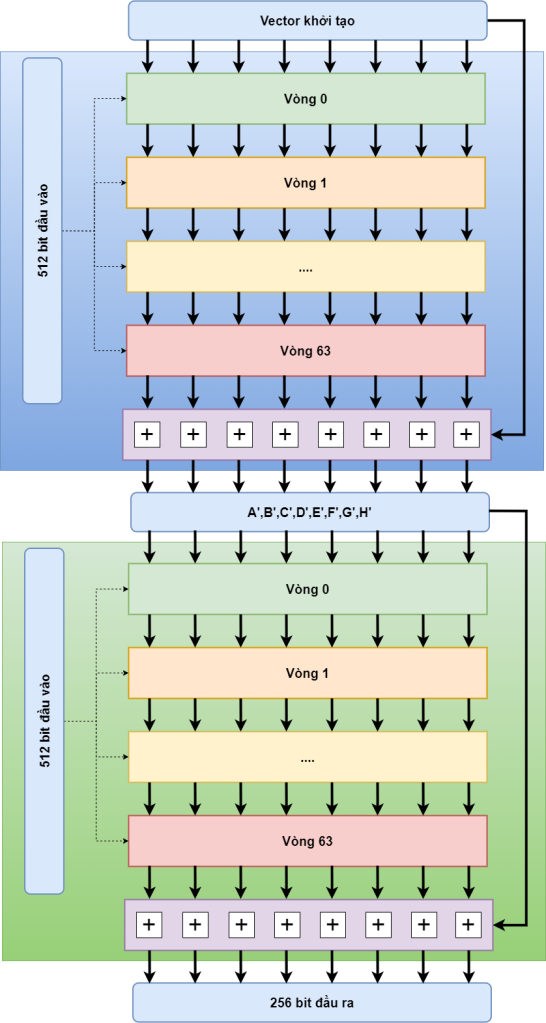
SHA2 và MD5

Độ dài hash

SHA2 có độ dài hash khác nhau. Với SHA256 thì độ dài là 256bit còn SHA512 thì là 512bit.

MD5 có độ dài hash là 128bit.

Tốc độ

Ta có thể thấy rõ rằng SHA2 phức tạp hơn MD5 rất nhiều, cùng chạy 64 vòng tất cả nhưng trong một vòng thì SHA2 có nhiều phép tính và phức tạp hơn. Do đó MD5 sẽ nhanh hơn SHA2.

Bảo mật

Như đã nói ở bài trước MD5 có thể bị tấn công va chạm, là khi đầu vào khác nhau nhưng ra mã hash lại giống nhau. Còn đối với SHA2 hiện tại không có biện pháp tấn công va chạm khả thi.

Sử dụng

MD5 thường được sử dụng cho kiểm tra toàn vẹn dữ liệu cơ bản (như kiểm tra lỗi trong truyền tải dữ liệu) nhưng không nên sử dụng cho các mục đích bảo mật nghiêm ngặt.

SHA2 thường được sử dụng trong các ứng dụng bảo mật, chứng thực, và trong các hệ thống yêu cầu độ bảo mật cao.

Kết bài

Tới đây là kết bài rồi, trong bài này mình đã điểm qua về hàm băm SHA256, đại diện cho họ băm SHA2. Hi vọng với bài này mình và mọi người sẽ cùng hiểu thêm một chút về cơ sở toán học, cách thức hoạt động của các thuật toán chúng ta vẫn thường sử dụng hằng ngày nha.

Cuối cùng là quà cho những bạn đã kiên trì mà đọc tới đây, mình tìm thấy một trang web demo rất hay về SHA256, mời các bạn cùng vọc nha: https://sha256algorithm.com/

Tài liệu tham khảo & công cụ

Link bài viết gốc https://truongphuoc.wordpress.com/2024/08/22/blockchain-20-5-ham-bam-sha256/

[Cryptography p12] Hàm băm SHA256