I. Giới thiệu chung

Trong các chuyên đề trước, tôi đã giới thiệu tới các bạn về hai cấu trúc dữ liệu ngăn xếp và hàng đợi, cùng với đó là kĩ thuật stack đơn điệu - một kĩ thuật ứng dụng của ngăn xếp. Cũng tương tự, hàng đợi sẽ có những ứng dụng riêng của nó. Trong chuyên đề này, tôi sẽ giới thiệu một bài toán ứng dụng cực kỳ quen thuộc và thường xuyên xuất hiện trong các kì thi lập trình ở cấp THCS - THPT của hàng đợi, đó là bài toán Loang trên ma trận. Về bản chất, phương pháp giải của bài toán này chính là giải thuật Tìm kiếm theo chiều sâu (BFS) trên đồ thị, tuy nhiên khi áp dụng trên ma trận thì lại khá dễ hiểu, nên các bạn chưa học về đồ thị vẫn có thể hiểu và làm được bài toán này.

Phát biểu bài toán

Cho một ma trận gồm $m$ hàng, $n$ cột, các hàng được đánh số từ $1$ tới $m$ từ trên xuống dưới, các cột được đánh số từ $1$ tới $n$ từ trái qua phải. Ô nằm trên giao của hàng $i,$ cột $j$ được gọi là ô $(i, j),$ trên ô đó có ghi số $0$ hoặc $1$ thể hiện có thể đi vào hoặc không thể đi vào nó. Bạn xuất phát từ ô $(x, y)$ và mỗi bước di chuyển có thể đi sang một trong bốn ô trên, dưới, trái, phải.

Hãy tìm đường đi ngắn nhất từ ô $(x_1, y_1)$ tới ô $(x_2, y_2)$ trên ma trận? Biết rằng, độ dài đường đi giữa hai ô được tính bằng tổng số lượng ô trên đường đi, tính cả hai ô xuất phát và kết thúc.

Input:

• Dòng đầu tiên chứa hai số nguyên dương $m, n$.
• $m$ dòng tiếp theo, mỗi dòng chứa một dãy gồm $n$ số thuộc hai giá trị $0 - 1$ thể hiện ma trận.
• Dòng cuối cùng chứa bốn số nguyên dương $x_1, y_1, x_2, y_2$.

Output:

• Dòng đầu tiên in ra số nguyên duy nhất là độ dài đường đi ngắn nhất giữa hai ô $(x_1, y_1)$ và $(x_2, y_2)$. Nếu không thể di chuyển được thì in ra $-1$.
• Nếu tồn tại đường đi ngắn nhất, thì các dòng tiếp theo in ra tọa độ các ô trên đường đi, bắt đầu là ô $(x_1, y_1)$ và kết thúc là ô $(x_2, y_2)$.

Sample Input:

5 5 0 1 0 0 0
0 0 1 0 1
0 0 0 1 0
0 1 0 0 0
0 1 0 0 1
1 1 5 3

Sample Output:

7
1 1
2 1
3 1
3 2
3 3
4 3
5 3

Phương pháp giải

Giả sử bạn đang đứng ở ô có tọa độ $(x, y),$ thì các tọa độ mà bạn có thể đến được theo đề bài là:

$$(x - 1, y); (x, y - 1); (x + 1, y); (x, y + 1)$$

Ý tưởng tiếp theo là sử dụng một hàng đợi để lưu danh sách các ô trên mọi đường đi có thể xuất hiện trên bảng, và đường đi nào tới được ô đích trước tiên thì đường đi đó sẽ là đường đi ngắn nhất. Để kiểm soát độ dài đường đi ngắn nhất tới một ô, ta sử dụng mảng $dp[x][y]$ nghĩa là độ dài đường đi ngắn nhất tính từ ô xuất phát $(x_1, y_1)$ tới ô $(x, y)$. Ban đầu chỉ có $dp[x_1][y_1] = 1$.

Ban đầu trong hàng đợi sẽ chỉ có duy nhất ô xuất phát $(x_1, y_1)$. Sau đó, quy trình thuật toán như sau:

• Lấy ra một ô $(x_0, y_0)$ ở đầu hàng đợi, coi như đang đứng ở ô đó. Việc đứng ở ô này sẽ phát sinh ra việc thăm $4$ ô gần nó nhất mà di chuyển tới được: $(x_0 - 1, y_0); (x_0 + 1, y_0); (x_0, y_0 - 1); (x_0, y_0 + 1);$ ta đưa tất cả các ô này vào cuối hàng đợi (nếu các ô đó hợp lệ), và cập nhật độ dài đường đi ngắn nhất tới các ô đó bằng $dp[x_0][y_0] + 1$.

• Loại bỏ ô ở đầu hàng đợi, tiếp tục lặp lại bước bên trên với ô mới ở đầu hàng đợi, giả sử là ô $(x_0', y_0')$. Việc thăm ô này sẽ phát sinh thăm các ô $(x_0' - 1, y_0'); (x_0' + 1, y_0'); (x_0', y_0' - 1); (x_0', y_0' + 1);$ nhưng rõ ràng chúng nằm ở "xa" ô xuất phát hơn so với các ô $(x_0 - 1, y_0); (x_0 + 1, y_0); (x_0, y_0 - 1); (x_0, y_0 + 1);$ nên chúng chỉ được xét đến sau khi các ô $(x_0 - 1, y_0); (x_0 + 1, y_0); (x_0, y_0 - 1); (x_0, y_0 + 1)$ đã bị loại hết khỏi hàng đợi. Vì vậy, thứ tự duyệt các ô sẽ là: $(x_0, y_0); (x_0 - 1, y_0); (x_0 + 1, y_0); (x_0, y_0 - 1); (x_0, y_0 + 1);(x_0' - 1, y_0'); (x_0' + 1, y_0'); (x_0', y_0' - 1); (x_0', y_0' + 1);\dots$

  <center>

  

  </center>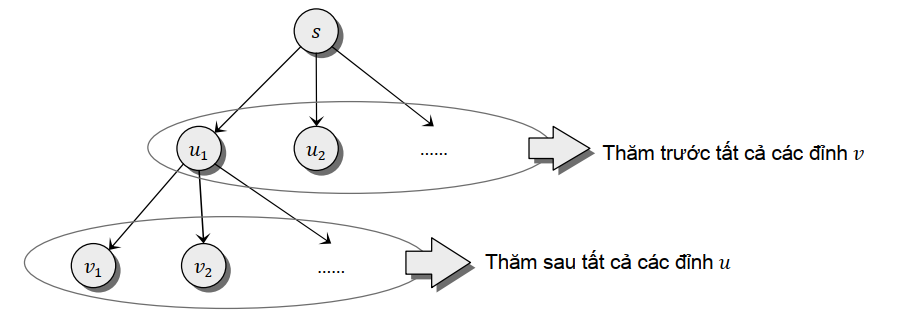

Do thứ tự duyệt các ô từ gần tới xa như vậy, nên ta có thể khẳng định, nếu như ô ở đầu hàng đợi là ô đích $(x_2, y_2)$, thì chắc chắn ô này đang nằm trên đường đi ngắn nhất từ $(x_1, y_1)$ tới đích. Cũng chính vì cách duyệt "tỏa" ra xung quanh như vậy, giống như vết dầu loang trên biển mà bài toán này được gọi là bài toán loang trên ma trận. Nói chính xác, nó là giải thuật Tìm kiếm theo chiều sâu trên đồ thị nhưng áp dụng với ma trận hai chiều.

Ngoài ra, một ô $(x, y)$ muốn được đưa vào hàng đợi, thì ô đó phải thỏa mãn các điều kiện sau:

• Chưa được thăm trong đường đi nào trước đó, tức là $dp[x][y] = 0$.
• Ô đó nằm trong bảng.
• Ô đó không mang số $1$.

Vậy ta thiết kế một hàm để kiểm tra một ô có hợp lệ hay không như sau:

is_valid(int x, int y): return x >= 1 and x <= m and y >= 1 and y <= m and dp[x][y] == 0 and a[x][y] == 0

Để thuận tiện hơn trong việc duyệt các ô kề với một ô, ta sẽ sử dụng một ma trận $\text{step}$ để lưu các bước đi có thể từ một ô. Trong bài toán này, do ta có bốn cách di chuyển với hệ số lần lượt là $(-1, 0); (1, 0); (0, -1); (0, 1)$ nên ma trận sẽ có kích thước $4 \times 2$: $\big\{\{1, 0\}; \{-1, 0\}; \{0, 1\}; \{0, -1\}\big\}$. Các bước đi từ một ô $(x, y)$ sẽ là $\big(x + step[i][0], y + step[i][1]\big); 0 \le i \le 3$.

Còn để truy vết, ta sử dụng một mảng hai chiều kiểu pair (tuple trong Python) $trace[x][y]$ để lưu tọa độ của ô liền trước ô $(x, y)$ trên đường đi ngắn nhất tới nó. Giá trị này được gán luôn khi đi từ một ô tới các ô xung quanh.

Đánh giá độ phức tạp

Do mỗi ô sẽ chỉ đi vào hoặc đi ra khỏi hàng đợi không quá một lần, nên độ phức tạp của giải thuật sẽ là $O(m \times n)$.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h> using namespace std; const int step[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}}; void enter(int &m, int &n, vector < vector < int > > &a, int &x1, int &y1, int &x2, int &y2)
{ cin >> m >> n; a = vector < vector < int > >(m + 1, vector < int >(n + 1)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) cin >> a[i][j]; cin >> x1 >> y1 >> x2 >> y2;
} // Kiểm tra một ô có phải hợp lệ hay không.
bool is_valid(int x, int y, int m, int n, vector < vector < int > > &dp, vector < vector < int > > &a)
{ return (1 <= x && x <= m && 1 <= y && y <= n && (!dp[x][[y]) && (!a[x][y]));
} void solution(int m, int n, vector < vector < int > > &a, int x1, int y1, int x2, int y2)
{ // Khai báo hàng đợi và các mảng lưu trữ. queue < pair < int, int > > qu; vector < vector < int > > dp(m + 1, vector < int >(n + 1, 0)); vector < vector < pair < int, int > > > trace(m + 1, vector < pair < int, int > >(n + 1)); dp[x1][y1] = 1; qu.push({x1, y1}); while (!qu.empty()) { pair < int, int > cur = qu.front(); qu.pop(); // Đã tìm ra kết quả, tới được ô đích thì dừng duyệt. if (cur.first == x2 && cur.second == y2) break; // Duyệt các ô có thể đến được từ ô hiện tại đang đứng. for (int i = 0; i <= 3; ++i) { int next_x = cur.first + step[i][0], next_y = cur.second + step[i][1]; // Nếu ô kế tiếp hợp lệ thì đưa nó vào hàng đợi. if (is_valid(next_x, next_y, m, n, dp, a)) { dp[next_x][next_y] = dp[cur.first][cur.second] + 1; trace[next_x][next_y] = cur; qu.push({next_x, next_y}); } } } // In kết quả. if (!dp[x2][y2]) cout << -1; else { cout << dp[x2][y2] << endl; vector < pair < int, int > > path; pair < int, int > cell = {x2, y2}; while (trace[cell.first][cell.second] != 0) { path.push_back(cell); cell = trace[cell.first][cell.second]; } cell.push_back({x1, y1}); for (int i = path.size() - 1; i >= 0; --i) cout << path[i].first << ' ' << path[i].second << endl; }
} main()
{ int m, n, x1, y1, x2, y2; vector < vector < int > > a; enter(m, n, a, x1, y1, x2, y2); solution(m, n, a, x1, y1, x2, y2);
}

Ngôn ngữ Python:

from collections import deque step = [[-1, 0], [1, 0], [0, -1], [0, 1]] # Nhập dữ liệu.
def enter(): m, n = map(int, input().split()) a = [[] for _ in range(m + 1)] for i in range(1, m + 1): a[i] = [0] + [int(j) for j in input().split()] x1, y1, x2, y2 = map(int, input().split()) return m, n, a, x1, y1, x2, y2 # Kiểm tra một ô có hợp lệ để đi vào không.
def is_valid(x, y, m, n, dp, a): return 1 <= x <= m and 1 <= y <= n and dp[x][y] == 0 and a[x][y] == 0 # Loang trên ma trận.
def solution(m, n, a, x1, y1, x2, y2): qu = deque(()) dp = [[0] * (n + 1) for _ in range(m + 1)] trace = [[(0, 0)] * (n + 1) for _ in range(m + 1)] dp[x1][y1] = 1 qu.append((x1, y1)) while len(qu) > 0: cur = qu[0] qu.popleft() if cur[0] == x2 and cur[1] == y2: break for i in range(4): next_x, next_y = cur[0] + step[i][0], cur[1] + step[i][1] if is_valid(next_x, next_y, m, n, dp, a): dp[next_x][next_y] = dp[cur[0]][cur[1]] + 1 trace[next_x][next_y] = cur qu.append((next_x, next_y)) if not dp[x2][y2]: return -1, 0, 0 else: path = [] cell = (x2, y2) while cell[0] != 0 and cell[1] != 0: path.append(cell) cell = trace[cell[0]][cell[1]] return 1, dp[x2][y2], path # Xử lý các trường hợp bài toán.
def main(): m, n, a, x1, y1, x2, y2 = enter() res, minimum_distance, path = solution(m, n, a, x1, y1, x2, y2) if res == -1: print(-1) else: print(minimum_distance) for i in range(len(path) - 1, -1, -1): print(path[i][0], path[i][1]) if __name__ == '__main__': main()

II. Một số bài toán áp dụng

1. Bồn hoa

Đề bài

Có một mảnh đất hình chữ nhật được chia thành các ô vuông, trên mỗi dòng có $n$ ô và trên mỗi cột có $m$ ô. Trên đó người ta xây dựng các bồn hoa, mỗi bồn hoa bao gồm các ô liên kết với nhau. Hai ô cùng nằm trên một bồn hoa nếu chúng có cùng chung cạnh.

Hãy xác định diện tích và chu vi của bồn hoa lớn nhất (mỗi ô vuông là một đơn vị đo diện tích, mỗi cạnh của ô vuông là một đơn vị đo chiều dài)?

Input:

• Dòng đầu tiên chứa hai số nguyên dương $m, n$ – kích thước mảnh đất.
• $m$ dòng tiếp theo, mỗi dòng ghi $n$ số nguyên dương $0$ hoặc $1,$ giữa hai số cách nhau một khoảng trống. Tại dòng $i,$ số thứ $j$ được ghi:
  • Số $0$ nếu ô ở dòng $i,$ cột $j$ không nằm trong bồn hoa nào.
  • Số $1$ nếu ô ở dòng $i,$ cột $j$ nằm trong bồn hoa nào đó.

Ràng buộc:

• $1 \le m, n \le 100$.

Output:

• Gồm hai số nguyên trên hai dòng lần lượt là diện tích của bồn hoa có diện tích lớn nhất và chu vi của bồn hoa có chu vi lớn nhất.

Sample Input:

7 10
0 1 1 1 0 0 0 0 1 1
1 1 1 0 0 0 0 0 0 1
0 1 1 1 1 0 1 1 1 0
0 0 0 0 0 0 0 1 0 0
0 0 1 1 0 0 0 0 0 0
0 1 1 1 0 1 1 1 0 0
0 0 1 0 0 1 0 0 0 1

Sample Output:

10
18

Ý tưởng

Mỗi ô $(i, j)$ mang số $1$ sẽ thuộc vào một bồn hoa. Xét mọi ô $(i, j)$ mang số $1,$ nếu ô đó chưa thăm thì sử dụng giải thuật loang để tìm kiếm từ ô đó tỏa ra tất cả các ô thuộc cùng bồn hoa với nó, đồng thời tính chu vi và diện tích của bồn hoa này và đánh dấu toàn bộ các ô trong bồn hoa đó đã thăm.

Mỗi lần thực hiện loang xong, lấy giá trị chu vi và diện tích lớn nhất.

Độ phức tạp: $O(m \times n)$.

Cài đặt

Ngôn ngữ C++: Ở code này sẽ định danh từ khóa first là x, second là y và pair < int, int > là II để viết code đỡ dài dòng.

#include <bits/stdc++.h>
#define task "Bonhoa."
#define x first
#define y second using namespace std; typedef pair < int, int > II;
const int step[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}}; void enter(int &m, int &n, vector < vector < int > > &a)
{ cin >> m >> n; // Khởi tạo trước ma trận gồm m + 2 hàng và n + 2 cột, để bảng có các đường // viền bên ngoài đều bằng 0, phục vụ cho việc tính chu vi. a = vector < vector < int > >(m + 2, vector < int >(n + 2)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) cin >> a[i][j];
} // Kiểm tra một ô next_pos có hợp lệ hay không.
bool is_valid(II next_pos, int m, int n, vector < vector < int > > &mark, vector < vector < int > > &a)
{ return (next_pos.x > 0 && next_pos.x <= m && next_pos.y > 0 && next_pos.y <= n && a[next_pos.x][next_pos.y] == 1 && mark[next_pos.x][next_pos.y] == 0);
} // Tính chu vi và diện tích của một bồn hoa.
void spread(II start, int m, int n, vector < vector < int > > &mark, vector < vector < int > > &a, int &area, int &perimeter)
{ queue < II > qu; mark[start.x][start.y] = 1; qu.push(start); while (!qu.empty()) { II cur_pos = qu.front(); ++area; qu.pop(); for (int i = 0; i <= 3; ++i) { II next_pos = {cur_pos.x + step[i][0], cur_pos.y + step[i][1]}; // Nếu ô bên cạnh ô hiện tại là một ô trống thì chu vi của bồn hoa sẽ tăng thêm 1 đơn vị. // Lưu ý nếu như ô hiện tại là một ô nằm trên đường viền của bảng, thì ô kề cạnh nó sẽ bị // nằm ngoài bảng. Ta khai báo trước mảng có thêm một hàng bên dưới và một cột bên trên // gồm toàn số 0 để tránh bị truy cập vào vị trí không tồn tại trên ma trận. if (a[next_pos.x][next_pos.y] == 0) ++perimeter; if (is_valid(next_pos, m, n, mark1, a)) { mark1[next_pos.x][next_pos.y] = 1; qu.push(next_pos); } } }
} // Xử lý các trường hợp bài toán.
void solution(int m, int n, vector < vector < int > > &a)
{ int max_area = 0, max_perimeter = 0; vector < vector < int > > mark(m + 1, vector < int >(n + 1)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) if (a[i][j] && !mark[i][j]) { int area = 0, perimeter = 0; spread({i, j}, m, n, mark, a, area, perimeter); max_area = max(max_area, area); max_perimeter = max(max_perimeter, perimeter); } cout << max_area << endl << max_perimeter;
} int main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int m, n; vector < vector < int > > a; enter(m, n, a); solution(m, n, a); return 0;
}

Ngôn ngữ Python:

from collections import deque step = [[-1, 0], [1, 0], [0, -1], [0, 1]] # Nhập dữ liệu.
def enter(): m, n = map(int, input().split()) # Khởi tạo trước ma trận gồm m + 2 hàng và n + 2 cột, để bảng có các đường viền ngoài cùng # đều bằng 0, phục vụ cho việc tính chu vi các bồn hoa. a = [[] for _ in range(m + 2)] a[0] = a[m + 1] = [0] * (n + 2) for i in range(1, m + 1): a[i] = [0] + [int(j) for j in input().split()] a[i] = a[i] + [0] return m, n, a # Kiểm tra một ô có hợp lệ hay không.
def is_valid(next_pos, m, n, mark, a): return 1 <= next_pos[0] <= m and 1 <= next_pos[1] <= n and a[next_pos[0]][next_pos[1]] and \ not mark[next_pos[0]][next_pos[1]] # Tính chu vi và diện tích của một bồn hoa.
def solution(start, m, n, mark, a): qu = deque() mark[start[0]][start[1]] = 1 qu.append(start) area, perimeter = 0, 0 while len(qu) > 0: cur = qu[0] qu.popleft() area += 1 for i in range(4): next_pos = (cur[0] + step[i][0], cur[1] + step[i][1]) # Nếu ô bên cạnh ô hiện tại là một ô trống thì chu vi của bồn hoa sẽ tăng thêm 1 đơn vị. # Lưu ý nếu như ô hiện tại là một ô nằm trên đường viền của bảng, thì ô kề cạnh nó sẽ bị # nằm ngoài bảng. Ta khai báo trước mảng có thêm một hàng bên dưới và một cột bên trên # gồm toàn số 0 để tránh bị truy cập vào vị trí không tồn tại trên ma trận. if not a[next_pos[0]][next_pos[1]]: perimeter += 1 if is_valid(next_pos, m, n, mark, a): mark[next_pos[0]][next_pos[1]] = 1 qu.append(next_pos) return area, perimeter # Xử lý các trường hợp bài toán.
def main(): m, n, a = enter() mark = [[0] * (n + 1) for _ in range(m + 1)] max_area, max_perimeter = 0, 0 for i in range(1, m + 1): for j in range(1, n + 1): if a[i][j] and not mark[i][j]: area, perimeter = solution((i, j), m, n, mark, a) max_area = max(max_area, area) max_perimeter = max(max_perimeter, perimeter) print(max_area) print(max_perimeter) if __name__ == '__main__': main()

2. Di chuyển trên sao hỏa

Đề bài

Một nhà du hành vũ trụ đang thám hiểm một vùng đất lạ trên sao Hỏa. Thông qua máy quét radar, bản đồ của vùng đất được mô tả như một bảng gồm $m$ dòng (đánh số từ $1$ tới $m,$ từ trên xuống dưới) và $n$ cột (đánh số từ $1$ tới $n,$ từ trái sang phải), mỗi ô $(i,j)$ của bảng thể hiện một khu vực của vùng đất và chứa một số nguyên $h_{i,j}$ là chiều cao của khu vực đó (do thiết kế đặc biệt của máy dò nên chiều cao của khu đất có thể hiển thị là một số nguyên âm). Nhà du hành muốn di chuyển từ khu vực $(x_1,y_1)$ tới khu vực $(x_2,y_2)$ của vùng đất. Để đảm bảo tính an toàn, nhà du hành chỉ di chuyển từ một khu vực tới bốn khu vực chung cạnh xung quanh nó, và ông ta sẽ di chuyển sao cho chênh lệch độ cao lớn nhất giữa hai khu vực liên tiếp trên đường đi là nhỏ nhất có thể.

Biết rằng, chênh lệch độ cao giữa hai khu vực được tính bằng giá trị tuyệt đối của hiệu chiều cao giữa hai nơi. Hãy xác định hành trình của nhà du hành?

Input:

• Dòng đầu tiên chứa hai số nguyên $m$ và $n$.
• Dòng thứ hai chứa bốn số nguyên dương $x_1,y_1,x_2,y_2$.
• $m$ dòng cuối cùng, dòng thứ $i$ chứa $n$ số nguyên $h_{i,j}$, mỗi số cách nhau một dấu cách.

Ràng buộc:

• $1≤m,n≤100$.
• $|h_{i,j}|≤10^9; \forall i, j: 1≤i≤m,1≤j≤n$.

Output:

• Một số nguyên duy nhất là độ chênh lệch lớn nhất giữa hai khu vực liên tiếp trên hành trình của nhà du hành.

Sample Input:

3 4
1 1 3 3
-2 9 3 4
0 3 7 -4
8 -9 9 10

Sample Output:

4

Giải thích:

Hành trình của nhà du hành như sau: $(1,1)→(2,1)→(2,2)→(2,3)→(3,3)$.

Ý tưởng

Nhận xét: Giả sử chênh lệch lớn nhất giữa hai ô liên tiếp trên $1$ đường đi từ $(x_1, y_1)$ tới $(x_2, y_2)$ là $X$. Nếu như tồn tại đường đi khiến cho $X \le K$ nào đó, thì cũng sẽ tồn tại đường đi khiến cho $X \le (K + 1)$. Do đó, bài toán này là một bài toán thỏa mãn định lý chính của Tìm kiếm nhị phân. Vậy ta sẽ tìm kiếm nhị phân giá trị $K$ nhỏ nhất.

Với mỗi giá trị $K$ trong quá trình tìm kiếm nhị phân, thực hiện loang tìm đường đi từ $(x_1, y_1)$ tới $(x_2, y_2)$ sao cho chênh lệch độ cao giữa hai ô liên tiếp luôn nhỏ hơn hoặc bằng $K$. Nếu tìm được đường đi như vậy thì giảm $K$ đi, ngược lại tăng $K$ lên cho tới khi tìm được $K$ nhỏ nhất.

Độ phức tạp: $O\big(\log(2 \times 10^9) \times (n + m)\big).$

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define task "MarMoving."
#define x first
#define y second using namespace std; typedef pair < int, int > II;
const int step[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; // Nhập dữ liệu.
void enter(int &m, int &n, int &x1, int &y1, int &x2, int &y2, vector < vector < int > > &h)
{ cin >> m >> n; cin >> x1 >> y1 >> x2 >> y2; h = vector < vector < int > >(m + 1, vector < int >(n + 1)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) cin >> h[i][j];
} // Kiểm tra một ô có hợp lệ hay không: Nằm trong bảng và chưa được thăm.
bool is_valid(int x, int y, int m, int n, vector < vector < bool > > &visited)
{ return (x > 0 && x <= m && y > 0 && y <= n && visited[x][y] == false);
} // Sử dụng loang để tìm đường đi ngắn nhất từ (x1, y1) tới (x2, y2) sao cho chênh lệch // độ cao giữa hai ô trên đường đi không vượt quá K (h_diff).
bool bfs_find_path(int m, int n, int x1, int y1, int x2, int y2, int h_diff, vector < vector < int > > &h)
{ queue < II > qu; vector < vector < bool > > visited(m + 1, vector < bool >(n + 1, false)); qu.push({x1, y1}); visited[x1][y1] = true; while (!qu.empty()) { II cur = qu.front(); qu.pop(); if (cur.x == x2 && cur.y == y2) return true; for (int i = 0; i <= 3; ++i) { int next_x = cur.x + step[i][0], next_y = cur.y + step[i][1]; if (!is_valid(next_x, next_y, m, n, visited)) continue; int next_diff = abs(h[cur.x][cur.y] - h[next_x][next_y]); if (next_diff <= h_diff) { visited[next_x][next_y] = true; qu.push({next_x, next_y}); } } } return false;
} // Xử lý bài toán.
void solution(int m, int n, int x1, int y1, int x2, int y2, vector < vector < int > > &h)
{ int minimum_diff = 0, l = 0, r = 2e9; // Tìm kiếm nhị phân giá trị K nhỏ nhất có thể. while (l <= r) { int mid = (l + r) >> 1; if (bfs_find_path(m, n, x1, y1, x2, y2, mid, h)) { minimum_diff = mid; r = mid - 1; } else l = mid + 1; } cout << minimum_diff;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int m, n, x1, y1, x2, y2; vector < vector < int > > h; enter(m, n, x1, y1, x2, y2, h); solution(m, n, x1, y1, x2, y2, h); return 0;
}

Ngôn ngữ Python:

from collections import deque step = [[-1, 0], [1, 0], [0, -1], [0, 1]] # Nhập dữ liệu.
def enter(): m, n = map(int, input().split()) x1, y1, x2, y2 = map(int, input().split()) h = [[] for _ in range(m + 2)] for i in range(1, m + 1): h[i] = [0] + [int(j) for j in input().split()] return m, n, (x1, y1), (x2, y2), h # Kiểm tra một ô có hợp lệ hay không: Nằm trong bảng và chưa được thăm.
def is_valid(next_pos, m, n, visited): return 1 <= next_pos[0] <= m and 1 <= next_pos[1] <= n and not visited[next_pos[0]][next_pos[1]] # Sử dụng loang để tìm đường đi ngắn nhất từ (x1, y1) tới (x2, y2) sao cho chênh lệch độ cao giữa
# hai ô liên tiếp trên đường đi không vượt quá K (chính là giá trị h_diff).
def find_path(start, destination, m, n, h_diff, h): qu = deque() visited = [[0] * (n + 1) for _ in range(m + 1)] visited[start[0]][start[1]] = 1 qu.append(start) while len(qu) > 0: cur = qu[0] qu.popleft() if cur == destination: return True for i in range(4): next_pos = (cur[0] + step[i][0], cur[1] + step[i][1]) if not is_valid(next_pos, m, n, visited): continue next_diff = abs(h[cur[0]][cur[1]] - h[next_pos[0]][next_pos[1]]) if next_diff <= h_diff: visited[next_pos[0]][next_pos[1]] = 1 qu.append(next_pos) return False # Xử lý bài toán.
def main(): m, n, start, destination, h = enter() minimum_diff = 0 # Tìm kiếm nhị phân giá trị K nhỏ nhất có thể. l, r = 0, 2e9 while l <= r: mid = int((l + r) // 2) if find_path(start, destination, m, n, mid, h): minimum_diff = mid r = mid - 1 else: l = mid + 1 print(int(minimum_diff)) if __name__ == '__main__': main()

III. Tài liệu tham khảo

• https://phattrienphanmem123az.com/lap-trinh-cpp-stl/cpp-stl-tim-hieu-va-su-dung-queue.html
• https://www.geeksforgeeks.org/breadth-first-search-or-bfs-for-a-graph/