I. Giới thiệu chung

Những bài toán trên mảng là chủ đề rất quen thuộc ở các kì thi lập trình. Mảng tổng tiền tố và Mảng hiệu là hai kĩ thuật bổ trợ, giúp đẩy nhanh tốc độ tính toán của một số thao tác trên mảng. Trong chuyên đề này, chúng ta sẽ cùng tìm hiểu về cách xây dựng và những ứng dụng của hai kĩ thuật nói trên.

1. Khái niệm

Mảng tổng tiền tố

Với mảng $A$ gồm $n$ phần tử $a_1, a_2, \dots, a_n;$ ta xây dựng một mảng $sum(A)$ theo quy tắc sau:

$sum[0] = c;$ với $c$ là một hằng số thực.
$sum[i] = sum[i - 1] + a_i; \forall i: 1 \le i \le n$ .

Khi đó, mảng $sum(A)$ được gọi là mảng tổng tiền tố (prefix sum array) của $A$ . Từ một mảng $A,$ ta có thể sinh ra vô số mảng $S(A)$ bằng cách chọn một hằng số $c$ tùy ý. Nhưng trên thực tế, ta thường chọn $c = 0$ để thuận tiện hơn khi tính toán.

</center>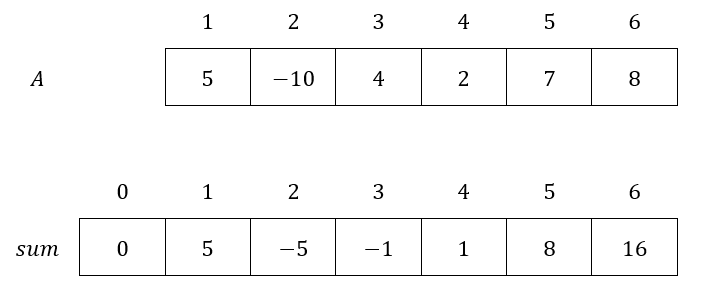

Mảng hiệu

Cũng với mảng $A,$ ta có thể xây dựng thêm một mảng $diff(A)$ theo quy tắc như sau:

$\begin{cases}diff[1] = a_1 \\ diff[i] = a_i - a_{i - 1}; \forall i: 2 \le i < n \end{cases}$

Mảng $diff(A)$ được gọi là mảng hiệu (difference array) của $A$ .

</center>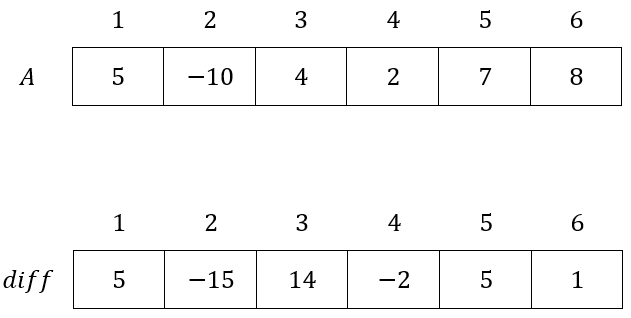

2. Phương pháp cài đặt

Mảng tổng tiền tố

Để xây dựng mảng tổng tiền tố, ta có thể áp dụng đúng định nghĩa để cài đặt trên mảng:

vector < int > build_prefix_sum(int n, int c, vector < int >& a)
{ vector < int > sum(n + 1); sum[0] = c; // Thường thì c = 0. for (int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + a[i]; return sum;
}

Hoặc ta có thể áp dụng hàm partial_sum() trong STL C++, cú pháp hàm này như sau:

partial_sum(first, last, result, binary_op);

Hàm này có ý nghĩa xây dựng tổng tiền tố cho các phần tử nằm trong phạm vi hai iterator [first, last) của một container, và trả mảng tổng tiền tố sang mảng kết quả, bắt đầu từ vị trí có iterator là result. Quá trình tính toán sẽ được thực hiện bằng toán tử binary_op (xem thêm minh họa về hàm này tại đây), nếu để trống thì mặc định là toán tử +:

vector < int > build_prefix_sum(int n, int c, vector < int >& a)
{ vector < int > sum(n + 1); sum[0] = c; // Thường thì c = 0. partial_sum(a.begin() + 1, a.end(), sum.begin() + 1); return sum;
}

Độ phức tạp của quá trình dựng mảng tổng tiền tố theo cả hai cách là $O(n)$ .

Mảng hiệu

Tương tự như mảng tổng tiền tố, ta cũng có thể xây dựng Mảng hiệu theo định nghĩa:

vector < int > build_diff_array(int n, vector < int >& a)
{ vector < int > diff(n + 1); diff[1] = a[1]; for (int i = 2; i <= n; ++i) diff[i] = a[i] - a[i - 1]; return diff;
}

Ngoài ra ta có thể sử dụng hàm adjacent_difference() được cung cấp bởi thư viện STL C++, với cú pháp như sau:

adjacent_difference(first, last, result, binary_op);

Hàm này sẽ thực hiện tính mảng hiệu cho các phần tử có iterator trong đoạn [first, last) của một container, và trả về mảng hiệu sang container từ vị trí có iterator là result. Tuy nhiên toán tử mặc định sử dụng trong hàm sẽ là toán tử - (xem thêm về hàm này tại đây):

vector < int > build_diff_array(int n, vector < int >& a)
{ vector < int > diff(n); adjacent_difference(a.begin() + 1, a.end(), diff.begin() + 1); return diff;
}

Độ phức tạp của quá trình xây dựng mảng hiệu theo hai cách trên đều là $O(n)$ .

3. Tính chất

Độ dài mảng

Mảng tổng tiền tố $sum(c, A)$ có thêm một phần tử phụ $sum[0] = c$ nên độ dài của nó sẽ nhiều hơn độ dài mảng gốc $1$ phần tử - tức là $n + 1$ .
Mảng hiệu lại được dựng bằng hiệu giữa hai phần tử kề nhau, mà chỉ có $n - 1$ cặp như vậy, nên độ dài của $diff(A)$ là $n$ (tính cả phần tử $diff[1] = a_1$ ).

Tính riêng biệt

Từ một mảng $A,$ với mỗi hằng số $c$ khác nhau ta lại tạo ra được một mảng tổng tiền tố khác nhau. Tuy nhiên, các mảng tổng tiền tố này chỉ khác nhau duy nhất ở giá trị $c$ .
Trái lại, cũng từ mảng $A$ đó, ta xây dựng được một và chỉ một mảng hiệu.

Liên hệ giữa Mảng tổng tiền tố và Mảng hiệu

Với mảng cộng dồn $sum(c, A)$ và mảng hiệu $diff(A),$ ta có thể khôi phục được mảng $A$ ban đầu thông qua hai cách:

$A = sum\big(0, diff(A)\big)$ .
$A = diff\big(sum(c, A)\big)$ với mọi giá trị $c \in \mathbb{R}$ .

Xem hình minh họa dưới đây để hiểu rõ mối liên kết nói trên:

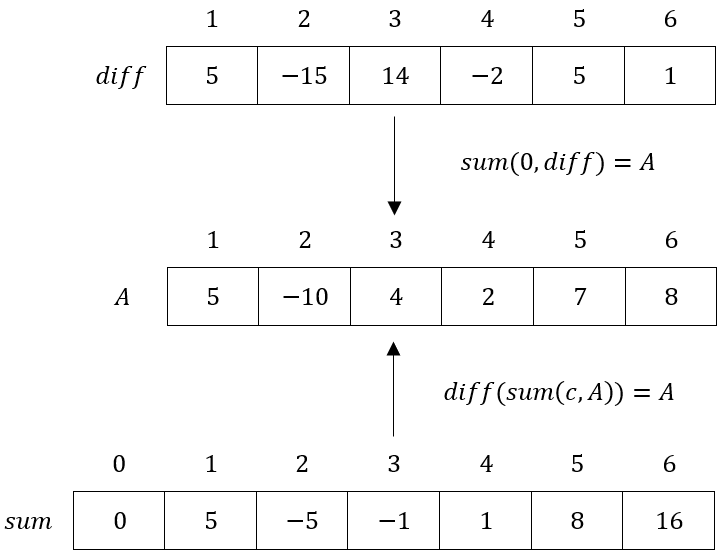
Hàm partial_sum() và adjacent_difference() trong C++ STL cũng tuân theo quy tắc nêu trên. Tuy nhiên, các thao tác trên hai hàm này có phần phức tạp hơn so với thao tác trên mảng mà ta cài đặt thủ công.

II. Ứng dụng của mảng tổng tiền tố

1. Ứng dụng cơ bản

Mảng tổng tiền tố có một ứng dụng quan trọng trong các bài toán trên dãy số. Kĩ thuật này giúp chúng ta tính nhanh ra tổng các số trên một đoạn trong thời gian chỉ $O(1),$ ứng dụng rất nhiều trong các bài toán lập trình thi đấu.

Nội dung bài toán cơ bản có thể phát biểu như sau:

Cho một dãy số $A$ gồm $n$ phần tử $a_1, a_2, \dots, a_n$ . Cần trả lời $Q$ truy vấn, mỗi truy vấn có dạng $(l, r)$ yêu cầu đưa ra tổng của các số có vị trí thuộc đoạn $[l, r]$ của dãy số.

Input:

Dòng đầu tiên chứa hai số nguyên dương $n$ và $Q$ - độ dài dãy số và số truy vấn.
Dòng thứ hai chứa $n$ số nguyên $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách.
Trên $Q$ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương $l$ và $r$ thể hiện một truy vấn.

Ràng buộc:

$1 \le n \le 10^6$ .
$1 \le Q \le 10^6$ .
$|a_i| \le 10^9; \forall i: 1 \le i \le n$ .

Output:

Ứng với mỗi truy vấn, in ra một số nguyên là tổng các số trong đoạn $[l, r]$ tương ứng. Kết quả mỗi truy vấn in ra trên một dòng.

Sample Input:

Sample Output:

15
9
3

Ý tưởng

Cách làm mà ai cũng có thể nhận ra là ứng với mỗi truy vấn, ta duyệt lại trên mảng từ vị trí $l$ tới vị trí $r$ và tính tổng:

$\sum_{i = l}^r a_i$

Cách làm này có độ phức tạp tổng quát là $O(n \times Q)$ . Do số truy vấn có thể lên tới $10^6,$ nên chắc chắn cách này bị chạy quá thời gian.

Ta sẽ xây dựng một mảng $sum[i]$ là tổng tiền tố của mảng $A$ .

Khi đó, tổng của các số thuộc đoạn $[l, r]$ trên mảng $A$ sẽ được tính theo công thức:

$sum[r] - sum[l - 1]$

Việc trừ này cũng sẽ khử đi hằng số $c,$ nên ta có thể áp dụng bất kì mảng tổng tiền tố nào được sinh ra từ $A$ để tính tổng đoạn con. Và nhờ vào công thức này, mỗi truy vấn có thể được trả lời chỉ trong $O(1)$ . Các bạn chỉ cần khởi tạo trước mảng tổng tiền tố trong $O(n)$ mà thôi. Do tính chất cộng từ trước ra sau, nên kĩ thuật này còn được gọi là mảng cộng dồn.

Cài đặt

#include <bits/stdc++.h> using namespace std; long long query(int l, int r, vector < long long >& sum)
{ return sum[r] - sum[l - 1];
} main()
{ int n, q; cin >> n; vector < long long > sum(n + 1, 0); for (int i = 1; i <= n; ++i) { long long x; cin >> x; sum[i] = sum[i - 1] + x; } while (q--) { int l, r; cin >> l >> r; cout << query(l, r, sum) << endl; } return 0;
}

2. Mảng tổng tiền tố hai chiều

Mảng tổng tiền tố có thể được phát triển lên để sử dụng trên các ma trận hai chiều kích thước $m \times n,$ dùng để tính tổng một hình chữ nhật con có kích thước bất kì trong ma trận đó, thông qua kĩ thuật Bao hàm - Loại trừ.

Bài toán được phát biểu khá tương tự:

Cho một ma trận $A$ kích thước $m \times n,$ các hàng được đánh số từ $1$ tới $m$ từ trên xuống, các cột được đánh số từ $1$ tới $n$ từ trái qua phải. Ô nằm trên giao của hàng $i,$ cột $j,$ gọi là ô $(i, j),$ trên đó có điền số nguyên $a_{i, j}$ .

Cần trả lời $Q$ truy vấn, mỗi truy vấn có dạng $(x_1, y_1, x_2, y_2)$ yêu cầu đưa ra tổng của các số thuộc hình chữ nhật có góc trái trên ở tọa độ $(x_1, y_1)$ và góc phải dưới ở tọa độ $(x_2, y_2)?$

Input:

Dòng đầu tiên chứa ba số nguyên dương $m, n$ và $Q$ - kích thước ma trận và số truy vấn.
Trên $m$ dòng tiếp theo, dòng thứ $i$ chứa $n$ số nguyên $a_{i, 1}, a_{i, 2}, \dots, a_{i, n}$ phân tách nhau bởi dấu cách - thể hiện hàng $i$ của ma trận.
Trên $Q$ dòng tiếp theo, mỗi dòng chứa bốn số nguyên dương $x_1, y_1, x_2, y_2$ thể hiện một truy vấn.

Ràng buộc:

$1 \le m, n \le 1000$ .
$1 \le Q \le 10^6$ .
$|a_{i, j}| \le 10^9; \forall i, j: 1 \le i \le m, 1 \le j \le n$ .

Output:

Ứng với mỗi truy vấn, in ra một số nguyên là tổng các số trong hình chữ nhật con tương ứng. Kết quả mỗi truy vấn in ra trên một dòng.

Sample Input:

5 4 3
1 3 2 4
5 7 8 9
1 4 2 5
2 4 -8 9
-5 -1 -2 -3
1 1 3 3
2 3 5 4
1 1 5 4

Sample Output:

33
20
47

Ý tưởng

Ta sử dụng một mảng $sum$ hai chiều để lưu tổng tiền tố của ma trận $A$ . Gọi $sum[i][j]$ là tổng các số thuộc hình chữ nhật có góc trái trên là $(1, 1),$ góc phải dưới là $(i, j)$ .

Giả sử ta cần tính tổng hình chữ nhật $(1, 1, i, j)$ như hình $1$ bên dưới:

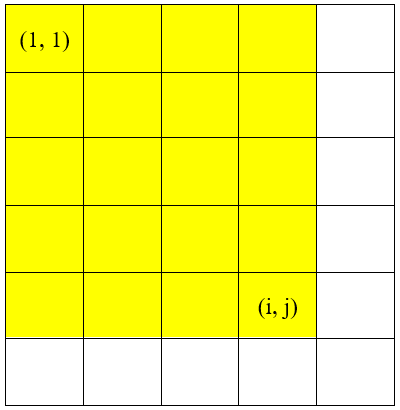
Hình 1

Nhận thấy, tổng hình chữ nhật $(1, 1, i, j)$ có thể được tạo thành bằng cách gộp tổng hai hình chữ nhật $(1, 1, i - 1, j)$ và $(1, 1, i, j - 1)$ lại, rồi cộng thêm giá trị $a_{i, j}$ :

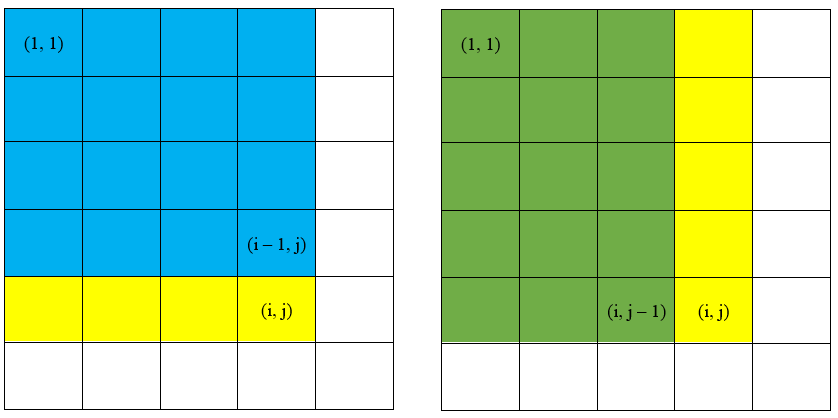
Hình 2

Tuy nhiên, như vậy thì tổng các số trong hình chữ nhật $(1, 1, i - 1, j - 1)$ sẽ bị tính thừa một lần, vì thế ta trừ bớt nó đi:

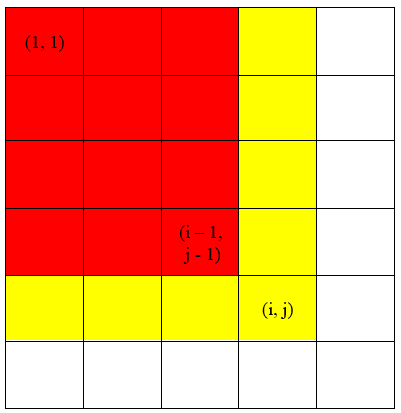
Hình 3

Tổng hợp lại công thức ở cả ba hình $1, 2, 3;$ ta rút ra công thức xây dựng $sum[i][j]$ :

$sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a_{i, j}; \forall i, j: 1 \le i \le m, 1 \le j \le n \ (1)$

Tiếp theo ta xây dựng công thức để tìm ra tổng của một hình chữ nhật con $(x_1, y_1, x_2, y_2)$ .

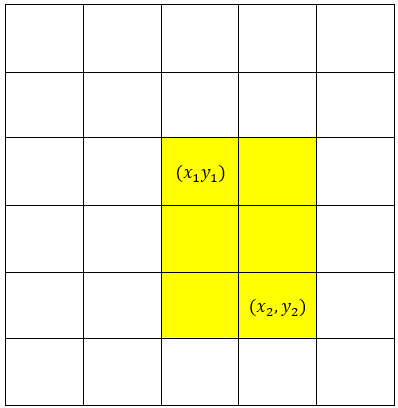
Hình 4

Nhận thấy, $sum[x_2][y_2]$ đã là tổng hình chữ nhật con $(1, 1, x_2, y_2)$ nên ta chỉ cần thêm bớt sao cho đạt được hình chữ nhật mong muốn. Ta sẽ trừ bớt đi tổng của hai hình chữ nhật con $(1, 1, x_1 - 1, y_2)$ và $(1, 1, x_2, y_1 - 1)$ :

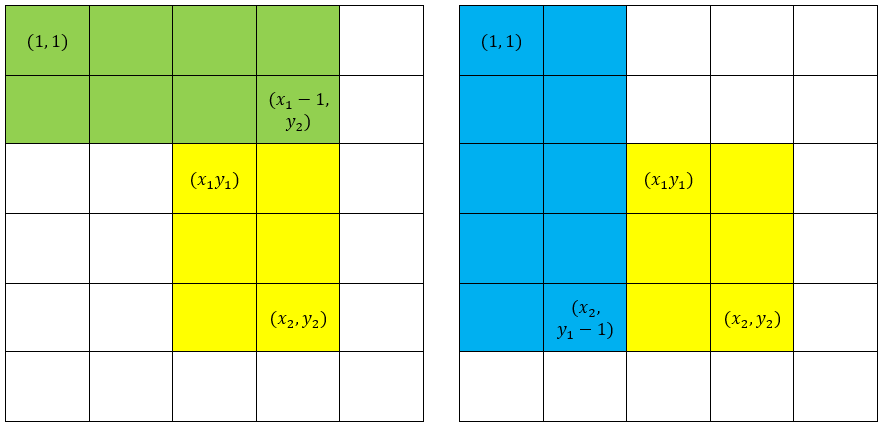
Hình 5

Tuy nhiên, phần hình chữ nhật $(1, 1, x_1 - 1, y_1 - 1)$ lại bị trừ thừa thêm $1$ lần. Do đó ta phải cộng lại một lần phần này vào kết quả.

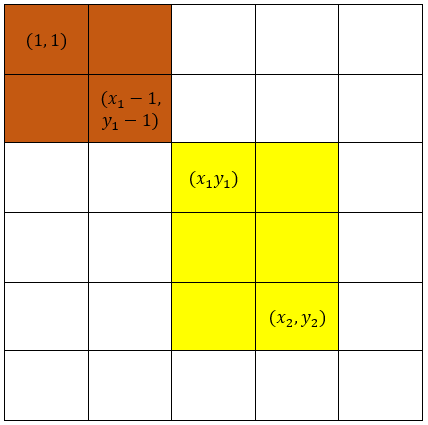
Hình 6

Tổng hợp lại công thức, ta có cách lấy tổng của một hình chữ nhật con $(x_1, y_1, x_2, y_2)$ như sau:

$sum[x_2][y_2] - sum[x_1 - 1][y_2] - sum[x_2][y_1 - 1] + sum[x_1 - 1][y_1 - 1] \ (2)$

Việc chuẩn bị trước mảng tổng tiền tố sẽ mất $O(m \times n),$ nhưng trả lời truy vấn thì chỉ còn $O(1)!$

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h> using namespace std; long long query(int x1, int y1, int x2, int y2, vector < vector < long long > >& sum)
{ return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
} main()
{ int m, n, q; cin >> m >> n >> q; vector < vector < long long > > sum(m + 1, vector < long long >(n + 1, 0)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) { int x; cin >> x; sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + x; } while (q--) { int x1, y1, x2, y2; cin >> x1 >> y1 >> x2 >> y2; cout << query(x1, y1, x2, y2, sum) << endl; }
}

3. Mảng tổng tiền tố 3 chiều (đọc thêm)

Giả sử ta có mảng trong không gian ba chiều $A$ với kích thước $m \times n \times p,$ thì mảng tổng tiền tố của nó được xây dựng theo quy tắc:

$sum_{i, j, k}(A)=\displaystyle \sum_{t_i\,=\,1}^{i} \sum_{t_j\,=\,1}^{j} \sum_{t_k\,=\,1}^{k} a_{t_i,t_j,t_k}$

Công thức sau được sử dụng để dựng mảng cộng dồn 3 chiều:

Tương tự, ta tính tổng các phần tử trong không gian $[x_1, x_2] \times [y_1, y_2] \times [z_1, z_2]$ thông qua Bao hàm - Loại trừ:

Ta cũng có thể áp dụng phương pháp này để mở rộng cho các mảng $n$ chiều. Tuy nhiên, do số lượng bài toán liên quan đến mảng trong không gian từ 4 chiều trở lên là cực hiếm, mảng cộng dồn trong không gian này gần như không có ứng dụng thực tiễn.

4. Một số bài tập minh họa

Bài toán 1: Phần thưởng

Đề bài

Bạn Hoa tham gia một trò chơi trên mạng và may mắn trở thành người chiến thắng. Tuy nhiên, luật trao thưởng của trò chơi này lại khá kì quặc. Các phần thưởng được xếp trên một bảng ô vuông đơn vị có kích thước $2 \times n,$ ô vuông nằm ở giao của hàng $i,$ cột $j$ chứa phần thưởng có giá trị là $a_{i, j}$ .

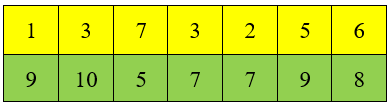
Minh họa bảng phần thưởng kích thước $2 \times 7$

Để nhận thưởng, Hoa sẽ phải điều khiển một nhân vật xuất phát từ vị trí $(1, 1)$ trên bảng ô vuông, đi tới ô $(2, n),$ và chỉ được sử dụng các bước đi xuống dưới hoặc sang phải. Tổng giá trị phần thưởng của các ô mà nhân vật đi qua sẽ là phần thưởng mà Hoa nhận được.

Yêu cầu: Hãy tính tổng giá trị phần thưởng lớn nhất mà Hoa có thể nhận được?

Input:

Dòng đầu tiên chứa số nguyên dương $n$ .
Hai dòng tiếp theo, mỗi dòng chứa $n$ số nguyên dương $a_{i, j}$ thể hiện một hàng của bảng phần thưởng.

Ràng buộc:

$1 \le n \le 10^5$ .
$1 \le a_{i, j} \le 10^9; \forall i, j: 1 \le i \le 2, 1 \le j \le n$ .

Output:

Số nguyên duy nhất là tổng giá trị phần thưởng lớn nhất mà Hoa nhận được.

Sample Input:

7
1 3 7 3 2 5 6
9 10 5 7 7 9 8

Sample Output:

Giải thích:

Các ô màu đỏ chính là đường đi mà Hoa sẽ chọn:

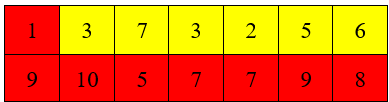
Ý tưởng

Nhận xét thấy, một khi Hoa đã di chuyển từ hàng thứ nhất xuống hàng thứ hai thì sẽ phải đi tiếp tới cuối hàng thứ hai, do chỉ được phép đi sang phải hoặc xuống dưới. Vì thế, kết quả bài toán sẽ là:

$\text{max}\left(\sum_{j = 1}^k a_{1, j} + \sum_{j = k}^n a_{2, j}\right); \forall k: 1 \le k \le n$

Với các bộ dữ liệu nhỏ, ta chỉ cần duyệt mọi vị trí $k,$ ứng với mỗi $k$ dùng thêm hai vòng lặp để tính tổng đoạn $a_{1,1 \dots k}$ và $a_{2, k \dots n}$ rồi lấy tổng lớn nhất làm kết quả. Độ phức tạp giải thuật là $O(n^2)$ .

Nhưng để làm được tối đa điểm của bài toán, cần xây dựng trước mảng tổng tiền tố $\text{prefix\_sum}[i][j]$ là tổng các số trên hàng $i$ từ cột $1$ tới cột $j$ . Sau đó, việc lấy tổng của đoạn $[1, k]$ trên hàng $1$ và đoạn $[k, n]$ trên hàng $2$ có thể thực hiện trong $O(1)$ với mỗi giá trị $k$ từ $1$ tới $n$ . Tới đây thu được giải thuật $O(n)$ .

Cài đặt

#include <bits/stdc++.h>
#define int long long using namespace std; const int maxn = 1e6 + 10;
typedef int matrix[3][maxn];
int n;
matrix prefix_sum; void enter()
{ cin >> n; for (int i = 1; i <= 2; ++i) for (int j = 1; j <= n; ++j) { int a; cin >> a; prefix_sum[i][j] = prefix_sum[i][j - 1] + a; }
} void solution()
{ int res = 0; for (int j = 1; j <= n; ++j) { int first_row_sum = prefix_sum[1][j]; int second_row_sum = prefix_sum[2][n] - prefix_sum[2][j - 1]; res = max(res, first_row_sum + second_row_sum); } cout << res;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(nullptr); enter(); solution(); return 0;
}

Bài toán 2: Hình vuông con

Đề bài

Một bảng hình chữ nhật được chia thành lưới ô vuông đơn vị kích thước $m \times n$ . Các hàng của bảng được đánh số từ $1$ tới $m,$ từ trên xuống dưới; các cột của bảng được đánh số từ $1$ tới $n,$ từ trái qua phải. Ô nằm trên hàng $i,$ cột $j$ của bảng được gọi là ô $(i,j)$ và có ghi giá trị $a_{i,j} \ (1≤i≤m,1≤j≤n)$ . Một hình vuông con của bảng là hình vuông chiếm chọn một số ô của bảng.

Yêu cầu: Với số nguyên dương $k$ cho trước, hãy chọn ra một hình vuông con kích thước $k \times k,$ sao cho giá trị của số nhỏ nhất trong hình vuông con là lớn nhất?

Input:

Dòng đầu tiên chứa ba số nguyên dương $m,n,k$ .
Trên $m$ dòng tiếp theo, dòng thứ $i$ chứa $n$ số nguyên dương $a_{i,1}, a_{i, 2}, \dots, a_{i, n}$ thể hiện hàng thứ $i$ của bảng số.

Ràng buộc:

$1 \le m, n \le 1000$ .
$1 \le k \le \text{min}(m, n)$ .
$1 \le a_{i, j} \le 10^6; \forall i: 1 \le i \le m$ .

Output:

Chứa một số nguyên duy nhất là giá trị của số nhỏ nhất trong hình vuông thỏa mãn yêu cầu của đề bài.

Sample Input:

Sample Output:

Giải thích:

Hình vuông con với tọa độ góc trái trên $(4, 4)$ và góc phải dưới $(5, 5)$ là hình vuông thỏa mãn đề bài.

Ý tưởng

Gọi giá trị của số nhỏ nhất trong hình vuông $k \times k$ tìm được là $minv$ .

Nếu gọi $check(minv)$ là một hàm kiểm tra có tồn tại hình vuông $k \times k$ nào mà giá trị nhỏ nhất là $minv$ hay không, thì ta thấy khi càng tăng $minv$ lên, khả năng hàm $check(minv) = \text{TRUE}$ càng giảm đi (vì $minv$ càng to thì càng khó tồn tại hình vuông $k \times k$ nhận nó làm giá trị nhỏ nhất). Từ đây, ta thấy $check(minv)$ là một hàm thỏa mãn Định lý chính của Tìm kiếm nhị phân, giá trị $minv$ lớn nhất thỏa mãn $check(minv) = \text{TRUE}$ có thể tìm được thông qua Tìm kiếm nhị phân trên tập kết quả.

Xét các giá trị $minv \in [1, 10^6],$ ta xây dựng hàm $check(minv)$ như sau:

Xây dựng một bảng hai chiều $B$ với ý nghĩa: Nếu $a_{i, j} \ge minv$ thì $b_{i, j} = 1,$ ngược lại $b_{i, j} = 0$ . Lúc này, nếu một ma trận con $k \times k$ trên bảng $A$ có giá trị nhỏ nhất là $minv$ thì tổng của ma trận con tương ứng trên bảng $B$ sẽ đúng bằng $k \times k$ (nghĩa là tất cả các số trong ma trận con đó đều $\ge minv$ ).
Xác định xem có tồn tại ma trận con $k \times k$ nào thỏa mãn tổng của ma trận con tương ứng trên bảng $B \ge k \times k$ hay không? Bước này ta có thể áp dụng quy hoạch động mảng tổng tiền tố hai chiều trên bảng $B$ .

Độ phức tạp: $O(m \times n \times \log)$ .

Cài đặt

#include <bits/stdc++.h> using namespace std; void enter(int &m, int &n, int &k, vector < vector < int > >& a)
{ cin >> m >> n >> k; a = vector < vector < int > >(m + 1, vector < int >(n + 1)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) cin >> a[i][j];
} int get_sum(int x1, int y1, int x2, int y2, vector < vector < int > >& sum)
{ return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
} // Tạo mảng s[i][j] là số lượng giá trị a[i][j] >= min_value
// trong hình chữ nhật (1, 1, i, j).
vector < vector < int > > create_table(int m, int n, vector < vector < int > >& a, int min_value)
{ // Tạo mảng tổng tiền tố s[i][j]. vector < vector < int > > s(m + 1, vector < int >(n + 1, 0)); for (int i = 1; i <= m; ++i) for (int j = 1; j <= n; ++j) s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + (a[i][j] >= min_value); return s;
} // Kiểm tra xem có tồn tại hình vuông k * k nào mà các số trong đó đều
// lớn hơn hoặc bằng min_value hay không.
bool check(int m, int n, int k, vector < vector < int > >& a, int min_value)
{ vector < vector < int > > sum = create_table(m, n, a, min_value); for (int i = 1; i <= m - k + 1; ++i) for (int j = 1; j <= n - k + 1; ++j) { int ii = i + k - 1, jj = j + k - 1; if (get_sum(i, j, ii, jj, sum) == k * k) return true; } return false;
} // Chặt nhị phân tìm giá trị nhỏ nhất tối đa trong các hình vuông kích thước k * k.
void solution(int m, int n, int k, vector < vector < int > >& a)
{ int l = 1, r = 1000000, res = 0; while (l <= r) { int mid = (l + r) / 2; if (check(m, n, k, a, mid)) res = mid, l = mid + 1; else r = mid - 1; } cout << res;
} int main()
{ ios_base::sync_with_stdio(false); cin.tie(nullptr); int m, n, k; vector < vector < int > > a; enter(m, n, k, a); solution(m, n, k, a); return 0;
}

Để tiếp tục theo dõi phần $2$ của series bài viết về Mảng tổng tiền tố và Mảng hiệu, mời các bạn nhấn vào đây.

Quy hoạch động 5.5: Mảng tổng tiền tố và Mảng hiệu (phần 1)

I. Giới thiệu chung

1. Khái niệm

Mảng tổng tiền tố

Mảng hiệu

2. Phương pháp cài đặt

Mảng tổng tiền tố

Mảng hiệu

3. Tính chất

Độ dài mảng

Tính riêng biệt

Liên hệ giữa Mảng tổng tiền tố và Mảng hiệu

II. Ứng dụng của mảng tổng tiền tố

1. Ứng dụng cơ bản

Ý tưởng

Cài đặt

2. Mảng tổng tiền tố hai chiều

Ý tưởng

Cài đặt

3. Mảng tổng tiền tố 3 chiều (đọc thêm)

4. Một số bài tập minh họa

Bài toán 1: Phần thưởng

Đề bài

Ý tưởng

Cài đặt

Bài toán 2: Hình vuông con

Đề bài

Ý tưởng

Cài đặt

Bình luận

Bài viết tương tự

Quy hoạch động - một thuật toán thần thánh

Series Data structures and algorithms

Phần 2.Thuật toán QUY HOẠCH ĐỘNG

Phần 1.Thuật toán QUY HOẠCH ĐỘNG

Quy hoạch động Bitmask

Quy hoạch động 5.5: Mảng tổng tiền tố và Mảng hiệu (phần 2)