Cấp số nhân hiểu ngay không cần nhớ công thức

Mở đầu

• Công thức tính tổng cấp số nhân là một trong những công thức mà nhiều bạn kêu là khó nhớ. Than trời trách đất, thậm chí là trách chính bản thân mình sao mà đầu óc kém thế 🤯

• Nhưng thực ra có cần phải nhớ làm gì đâu 🤷‍♂️ Chỉ cần suy luận logic là hiểu ra vì sao ta lại có công thức đó mà 🤏

• Đó cũng là con đường mà mình đang theo đuổi, cố gắng tìm hiểu rõ bản chất của vấn đề, chứ không thể tin vào trí nhớ ngày càng mai một theo tuổi tác của mình được 🕵️‍♂️

• Ngoài ra ở cuối bài viết này, mình cũng kể với các bạn một câu chuyện mầm non giải trí liên quan đến cấp số nhân, mong là các bạn sẽ thích 🫶

• Nếu thấy hay thì ủng hộ mình 1 like, 1 share, 1 follow để cho mình nhìn thấy động lực phía trước nhé 🛤

• Các bạn có thể xem phiên bản video của bài viết này tại đây:

Định nghĩa Cấp số nhân (tiếng Anh là Geometric Progression)

• Cấp số nhân là dãy số thỏa mãn điều kiện: kể từ số thứ 2, mỗi số sẽ đều là tích của số đứng ngay trước nó với một số không đổi.

• Trong Toán học, hằng số này thường được viết tắt là r (viết tắt của từ common ratio - tức là 1 tỉ số chung), hay tiếng Việt còn gọi là công bội của cấp số nhân.

  

• Ví dụ ta có dãy số:

  1, 3, 9, 27, 81
  

  là một cấp số nhân với hằng số ratio r = 3, bởi vì các phần tử trong dãy lần lượt là:

  1 x 3 = 3
  

  3 x 3 = 9
  

  9 x 3 = 27
  

  27 x 3 = 81
  

• Để tính tổng tất cả các phần tử của một cấp số nhân, chúng ta có thể sử dụng công thức:

  

  r phải khác 1 bởi vì: nếu r = 1 thì mẫu số của công thức này sẽ là:

  1 - 1 = 0, như vậy thì phép chia sẽ bị sai.

• Thực ra, đối với trường hợp r = 1, thì dãy số sẽ là các số a liên tiếp nhau, vì a nhân với 1 thì luôn bằng a, nên tổng của dãy số sẽ là n số a cộng với nhau, và bằng n x a.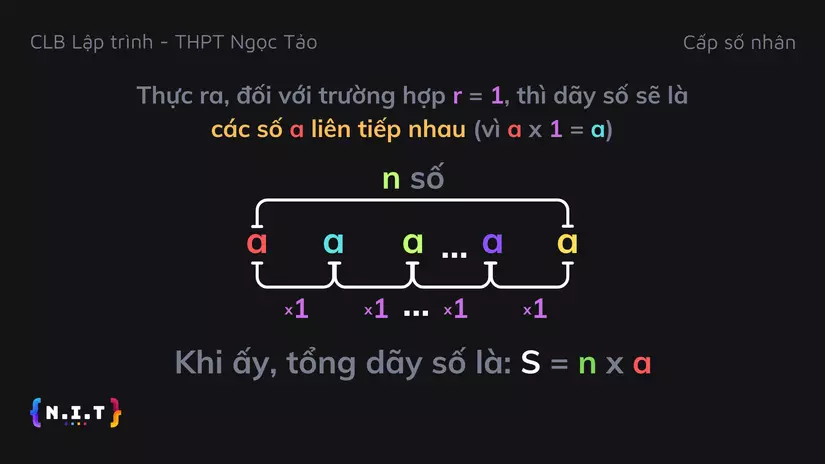

  

• Rồi bây giờ mình quay lại ví dụ lúc nãy: Dãy số 1, 3, 9, 27, 81 với hằng số ratio r = 3. Ta sẽ tính được tổng của dãy số này theo công thức là: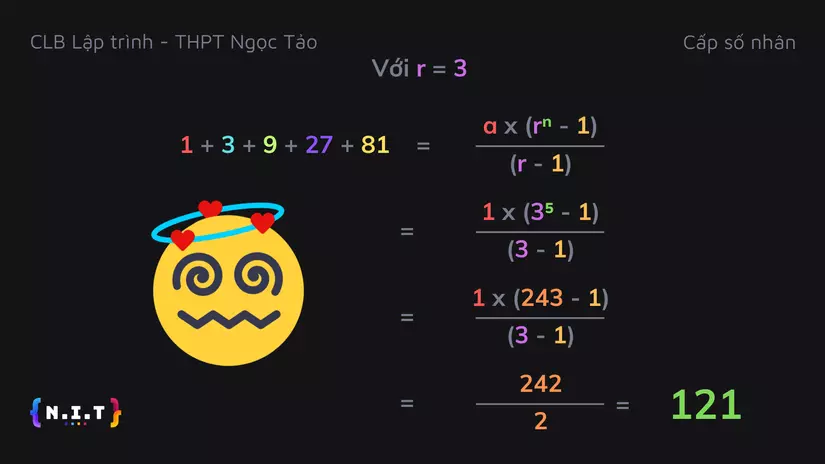

  

• Nếu thấy công thức này khó nhớ, thì mình sẽ chỉ cho các bạn cách làm như sau để suy ra được công thức, mà không cần học gạo, học vẹt nữa.

Suy luận logic để suy ra công thức

• Theo định nghĩa về cấp số nhân, kể từ số thứ 2 trong dãy số, mỗi số sẽ đều là tích của số đứng ngay trước nó, với một số hằng số ratio (viết tắt là r). Tức là:

  • Số đầu tiên là a, hằng số ratio là r

  • Số thứ hai là: a x r

  • Số thứ ba là: (a x r) x r (tức là lấy số thứ hai ở trên (a x r) nhân tiếp với hằng số r). Nếu phá ngoặc ra ta có thể viết thành: a x r²

  • Số thứ tư là: (a x r²) x r (tức là lấy số thứ ba ở trên (a x r²) nhân tiếp với hằng số r). Nếu phá ngoặc ra ta có thể viết thành: a x r³

  • ...

  • Số thứ n - 1 là: (a x rⁿ⁻³) x r = a x rⁿ⁻²

  • Số cuối cùng (số thứ n) là: (a x rⁿ⁻²) x r = a x rⁿ⁻¹

• Lý do mình biết được những số cuối cùng của dãy số như trên là vì:

  • Dãy này gồm n số, trong đó số đầu tiên là a, hoặc các bạn có thể hiểu là a x r⁰, vì r⁰ = 1, nên ta viết gọn lại thành a

  • Tương tự như vậy số tiếp theo là a x r¹, vì r¹ = r, nên ta viết gọn lại thành a x r

  • Tức là số mũ của r sẽ tăng dần từ 0, 1, 2, ..., cho đến n-1, thì sẽ đủ n số trong dãy.

• Khi ấy, tổng của dãy số này là: S (viết tắt của Sum)

  S = a + (a x r) + (a x r²) + (a x r³) + ... + (a x rⁿ⁻³) + (a x rⁿ⁻²) + (a x rⁿ⁻¹)
  

  Mình gọi đây là phương trình 1️⃣

• Bây giờ mình sẽ lấy cả 2 vế của phương trình 1️⃣ nhân với r, khi đó:

  S x r = r x [a + (a x r) + (a x r²) + (a x r³) + ... + (a x rⁿ⁻³) + (a x rⁿ⁻²) + (a x rⁿ⁻¹)]
  

• Nhân phá ngoặc ra chúng ta sẽ được:

  S x r = (a x r) + (a x r²) + (a x r³) + ... + (a x rⁿ⁻²) + (a x rⁿ⁻¹) + (a x rⁿ)
  

  Mình gọi đây là phương trình 2️⃣

• Lấy phương trình 2️⃣ trừ phương trình 1️⃣ ta được:

  (S x r) - S = (a x rⁿ) - a
  

  Vì nếu để ý các bạn sẽ thấy: Khi trừ vế bên phải của phương trình 2️⃣ cho phương trình 1️⃣, có các phần tử được triệt tiêu nhau như (a x r), (a x r²), ..., cho đến (a x rⁿ⁻¹)

  Vậy là vế phải sẽ chỉ còn lại là: (a x rⁿ) - a

• Rút gọn 2 vế ta sẽ được là:

  S x (r - 1) = a x (rⁿ - 1)
  

• Chuyển vế (r - 1) sang bên phải, ta sẽ suy ra được công thức tính tổng của cấp số nhân là:

  

  Trong đó:

  • a là số đầu tiên trong dãy,

  • r là hằng số ratio

  • n là số phần tử trong dãy

• Và đây chính là cách suy luận logic, giúp các bạn không còn phải học gạo, học vẹt cách tính tổng của cấp số nhân nữa.

• Nếu các bạn cũng là một người hay quên giống mình, thì đây chắc chắn là một cách rất hay để khắc phục việc đó.

Câu chuyện bàn cờ vua và những hạt thóc

• Có một câu chuyện rất nổi tiếng về việc áp dụng cấp số nhân, đó là câu chuyện về bàn cờ vua và những hạt thóc

  

• Sau khi nhà thông thái sáng tạo ra bàn cờ vua 8x8 tức là tổng cộng 64 ô, ông đã được nhà vua gọi vào triều để ban thưởng. Nhà thông thái đã trả lời nhà vua rằng: "Thần không cần gì nhiều, thần chỉ muốn xin thóc"

  

• Nhà vua còn tưởng mình đang nghe nhầm, cứ nghĩ nhà thông thái thông minh lắm, thế mà lại chỉ xin được thưởng thóc, thứ mà vừa rẻ, vừa nhiều ở vương quốc của ông.

  

• Nhà vua gật đầu đồng ý và hỏi nhà thông thái muốn được thưởng bao nhiêu thóc.

• Nhà thông thái nhẹ nhàng nói: "Dạ, thần chỉ muốn xin số thóc xếp đủ vào tất cả các ô trong bàn cờ vua theo quy luật: ô liền sau, sẽ có số hạt thóc gấp đôi ô liền trước. Và ô đầu tiên sẽ chỉ cần 1 hạt thóc."

  

• Nhà vua nghe xong thì càng tức giận hơn, nghĩ mình đã nhìn nhầm người tài, hay tên này đang muốn giễu cợt mình. Ô thứ nhất chỉ cần 1 hạt thóc, vậy ô thứ hai nhân đôi sẽ là 2 hạt, ô thứ ba là 4 hạt. "Thực sự quá coi thường vương quốc của ta."

  

• Nhưng vì nể tình tên này đã tạo ra bàn cờ vua rất độc đáo, nên nhà vua đã sai người hầu đem thóc ra xếp cho mau, để đuổi tên nhà thông thái dởm này đi cho khuất mắt.

• Người hầu nhận lệnh bắt đầu đem thóc vào xếp lên các ô vuông.

• Quá trình đầu tiên thoạt nhìn khá đơn giản, ô thứ nhất xếp 1 hạt, ô thứ hai xếp 2 hạt, ô thứ ba xếp 4 hạt, ô thứ tư xếp 8 hạt.

• Nhưng rồi tên người hầu cứ đếm mãi, xếp mãi, thậm chí là rủ cả những tên người hầu khác vào cùng đếm, mà mất mấy ngày trời mới chỉ xếp chưa được nổi 1 nửa bàn cờ. Bởi vì, khi đến ô số 21, số hạt thóc phải đếm đã lên đến hơn 1 triệu hạt.

  

• Những tên người hầu hoa mắt chóng mặt liền cầu xin nhà vua vì không thể tiếp tục được nữa.

• Nhà vua lúc này mới tá hỏa phát hiện ra, nếu cứ theo quy luật mà nhà thông thái kia đưa ra, ô liền sau có số hạt thóc gấp đôi ô liền trước, thì ô thứ 64 sẽ lên tới 2⁶³ hạt thóc, tức là khoảng 9 tỷ tỷ hạt.

  

• Đó là chưa kể còn phải gom số thóc của 63 ô còn lại nữa. Ước tính con số khi quy đổi sang khối lượng, sẽ phải lên đến hơn gần 600 tỷ tấn thóc.

  

• Trong khi trung bình 1 năm, cả thế giới cũng chỉ sản xuất ra được khoảng 3 tỷ tấn thóc. Vậy là để đáp ứng được số thóc theo quy luật mà nhà thông thái yêu cầu, toàn bộ loài người cần sản xuất trong khoảng 2 thế kỷ.

  

• Ví dụ ở trên chính là bài toán điển hình của cấp số nhân với hằng số ratio r = 2.

• Và đó cũng chính là lý do tại sao thiên tài Albert Einstein đã từng nói: "Lãi suất kép là kỳ quan thứ 8 của thế giới"

  

Hi vọng kiến thức này hữu ích với bạn. Hẹn gặp lại 👋