Lý thuyết tập hợp (Set theory)

Mở đầu

• Lý thuyết tập hợp (hay Set theory), là một trong những kiến thức nền tảng quan trọng không chỉ trong môn Toán thời học sinh, hay Toán rời rạc hồi sinh viên, mà còn là một kiến thức quan trọng trong lập trình thi đấu 🏆

• Qua bài viết này, mình cũng sẽ chia sẻ với các bạn những thuật ngữ chuyên ngành bằng Tiếng Anh thường xuyên được sử dụng trong các tài liệu nói chung và các đề thi lập trình thi đấu nói riêng, liên quan đến lý thuyết tập hợp 📝

• Các bạn có thể xem phiên bản video của bài viết này tại đây:

Set

• Tập hợp tiếng Anh gọi là Set.

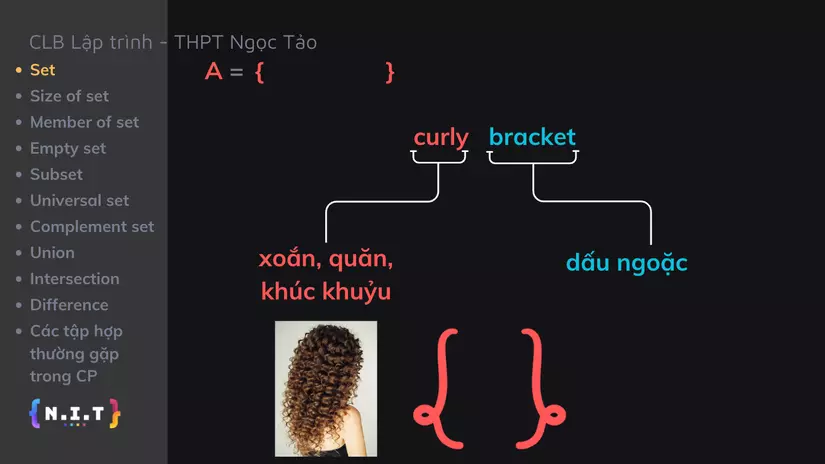
• Ký hiệu của 1 tập hợp thường là một cặp dấu ngoặc nhọn { }

• Nếu các bạn hay đọc những tài liệu hoặc xem video tiếng Anh, sẽ thấy họ hay dùng từ "curly bracket" để chỉ dấu ngoặc nhọn, tại vì "bracket" nghĩa là dấu ngoặc, còn "curly" nghĩa là xoắn, quăn, khúc khuỷu, giống như hình dấu ngoặc nhọn mà chúng ta hay viết luôn.

  

• Ví dụ: Mình có 1 tập hợp là:

  A = { n: n ∈ N, 1 ≤ n ≤ 5 }
  

  Tức là lúc này chúng ta có 1 tập hợp A gồm các số tự nhiên từ 1 đến 5, hay chúng ta có thể viết đầy đủ ra là:

  A = { 1, 2, 3, 4, 5 }
  

Size of set/Cardinality

• Tiếp theo là khái niệm size of set, hay có những tài liệu chuyên ngành khác gọi là cardinality, tức là số lượng phần tử có trong tập hợp.

• Ví dụ tập hợp A = { 1, 2, 3, 4, 5 } gồm có 5 phần tử.

• Và chúng ta sẽ có 2 cách để ký hiệu:

  • Cách 1: sử dụng 2 dấu | |, giống như ký hiệu giá trị tuyệt đối của 1 số mà chúng ta đã học ấy.

    |A| = 5 tức là số phần tử của A là 5.

  • Cách 2: n(A) = 5, trong đó n là viết tắt của number of elements.

Member of set

• Khái niệm kế tiếp là member of set hoặc element of set.

• Ký hiệu là: ∈

  • Tiếng Việt chúng ta thường gọi là "thuộc", chắc các bạn đã quen rồi, còn dịch word-by-word thì chúng ta có thể hiểu là "phần tử của tập hợp".

• Ví dụ với tập hợp A = { 1, 2, 3, 4, 5 }:

  • Nếu chúng ta có 1 element là x = 2, thì chúng ta có thể ký hiệu là x ∈ A, vì số 2 có xuất hiện ở trong tập hợp A.

  • Còn nếu chúng ta có 1 element khác là y = 6, thì chúng ta sẽ ký hiệu là y ∉ A, vì số 6 không hề xuất hiện trong tập hợp A.

Empty set

• Rồi đến empty set, dịch sang tiếng Việt có nghĩa là tập rỗng.

• Hiểu đơn giản thì tập rỗng là 1 tập hợp không có phần tử nào cả.

• Ký hiệu:

  • Chúng ta có thể viết là B = {}, tức là trong tập hợp này ko có phần tử nào hết.

  • Hoặc 1 cách ký hiệu khác quan thuộc hơn đó là B = ∅

Subset

• Tiếp đến là khái niệm subset, tức là tập con.

• Ký hiệu là: ⊂

• Ví dụ mình có 2 tập hợp:

  A = { 1, 2, 3, 4, 5 }
  

  B = {1, 2, 3}
  

• Lúc này B được gọi là một subset của A. Tức là mọi phần tử của tập hợp B đều có trong tập hợp A, nên B gọi là tập con của A.

  

• Và đương nhiên tập rỗng (∅) cũng là 1 tập con của A, và tập rỗng (∅) cũng là tập con của B luôn.

• Do vậy chúng ta cũng có 1 tính chất của tập rỗng, đó là: Tập rỗng (∅) là tập con của mọi tập hợp.

• Ví dụ mình có 1 tập hợp khác là:

  X = {0, 1, 2}
  

• Khi này X sẽ không phải là tập con của A (ký hiệu: X ⊄ A), bởi vì trong X có phần tử 0 không xuất hiện trong tập hợp A.

• Vậy nên các bạn hãy nhớ: Một tập hợp sẽ là tập con của 1 tập hợp khác, khi và chỉ khi nó nằm trọn vẹn bên trong tập hợp kia (giống như hình vẽ minh họa của tập hợp A và B ở trên)

• Một điều quan trọng nữa chúng ta cần nhớ, đó là: Một tập hợp sẽ luôn có 2^|size of set| tập con (bao gồm cả empty set ∅)

• Ví dụ tập hợp B = { 1, 2, 3 } sẽ có tổng cộng 2^|B| = 2³ = 8 subset, bao gồm:

  ∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
  

Universal set

• Tiếp theo là khái niệm universal set

  • universal nghĩa là thế giới, nhưng mà nếu dịch sang tiếng Việt là tập thế giới thì nó hơi buồn cười nhỉ.

  • Thế nên các thầy cô đã sử dụng một từ hay hơn trong Toán học, gọi là không gian mẫu.

• Đó, các bạn có thể thấy rất nhiều khái niệm quen thuộc mà chúng ta đã học trong môn Toán từ nhỏ xuất hiện trong bài viết này. Tuy nhiên, mình cũng muốn giới thiệu với các bạn biết về những thuật ngữ tiếng Anh của nó, để khi đọc tài liệu tiếng Anh có thể dễ dàng hiểu hơn.

• Universal set được ký hiệu là: u (chữ u viết thường), để tí nữa còn phân biệt với một khái niệm khác là Union - viết tắt là ∪ (giống như chữ U viết hoa).

• Và các bạn có thể thấy từ nãy tới giờ, mình đang lấy tập hợp A làm không gian mẫu của những ví dụ mình đưa ra.

• Do đó các bạn có thể hiểu universal set sẽ phụ thuộc vào bài toán mà mình đang nói đến.

Complement set

• Ví dụ mình có 1 universal set là:

  u = {1, 2, 3, 4, 5}
  

• Và bên trong nó mình có 1 subset là:

  A = {1, 2, 3}
  

• Khi ấy, mình có thể chỉ ra complement set của A là tập hợp những phần tử thuộc universal set mà không xuất hiện trong tập A.

  

  Mọi phần tử nằm trong vùng màu xanh dương ở đây chính là các phần tử thuộc complement set của A, cụ thể nó sẽ bao gồm số 4 và số 5.

• Khái niệm này mình nhớ đã từng học ở môn Toán rời rạc, và các thầy gọi nó là "Phần bù".

• Có 2 cách để ký hiệu complement set là: A^c (A mũ c) hoặc A và dấu gạch ngang ở trên đầu. Các bạn có thể xem ở hình minh họa bên trên.

Union

• Khái niệm union, dịch sang tiếng Việt là hợp nhất, thống nhất, tức là chúng ta sẽ gộp 2 tập hợp lại với nhau.

• Ký hiệu của union: ∪ (giống như chữ U viết hoa)

• Ví dụ: chúng ta có 1 universal set là hình chữ nhật như ở dưới đây:

  u = { 1, 2, 3, 4, 5 }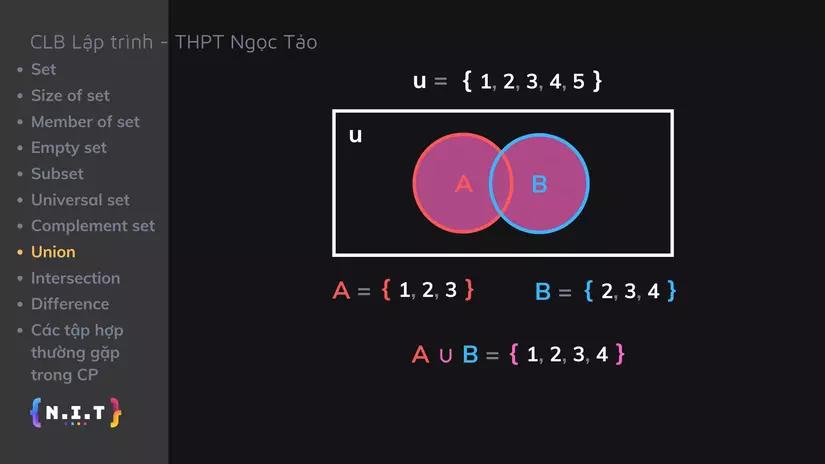
  

  

• Bên trong nó chúng ta có 2 tập con là A = {1, 2, 3} và B = {2, 3, 4}

• Khi đó, union của A và B sẽ là toàn bộ các phần tử của cả A và B hợp lại với nhau, mỗi phần tử chỉ được tính 1 lần.

• Tức là A ∪ B = {1, 2, 3, 4}. Chính là phần màu hồng được tô ở hình minh họa phía trên.

• Cách để các bạn nhớ ký hiệu này, đơn giản là chữ ∪ là viết tắt của Union.

Intersection

• Thế còn intersection thì sẽ được ký hiệu là ∩ (giống như chữ U viết ngược), tức là phần giao thoa giữa A và B.

• Nếu các bạn học tiếng Anh thì có thể đã gặp những trường hợp minh họa về ngã ba, ngã tư giao nhau trên đường ấy, người ta gọi là intersection.

  

• Ví dụ ta có 1 universal set là hình chữ nhật như ở dưới đây:

  u = { 1, 2, 3, 4, 5 }
  

• Bên trong nó chúng ta có 2 tập con là A = {1, 2, 3} và B = {2, 3, 4}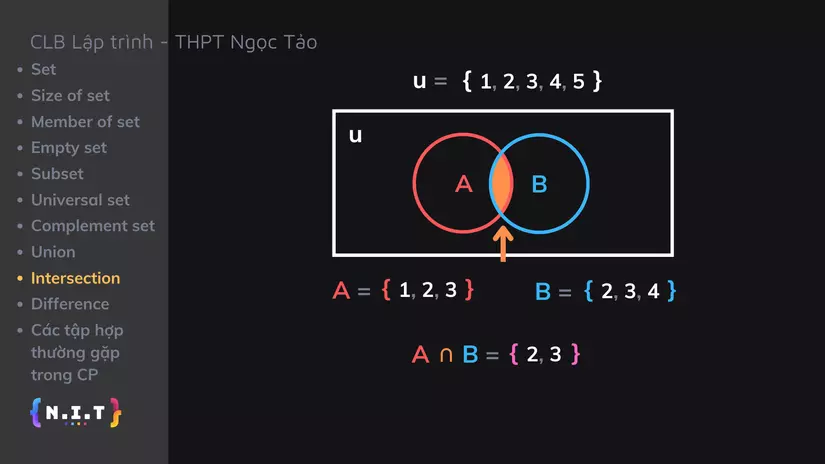

  

• Thì intersection của A và B chính là phần màu cam ở giữa A và B, tức là A ∩ B = {2, 3}

• Trường hợp đặc biệt:

  • Nếu A và B không có điểm chung, giống như hình vẽ ở đây:

    

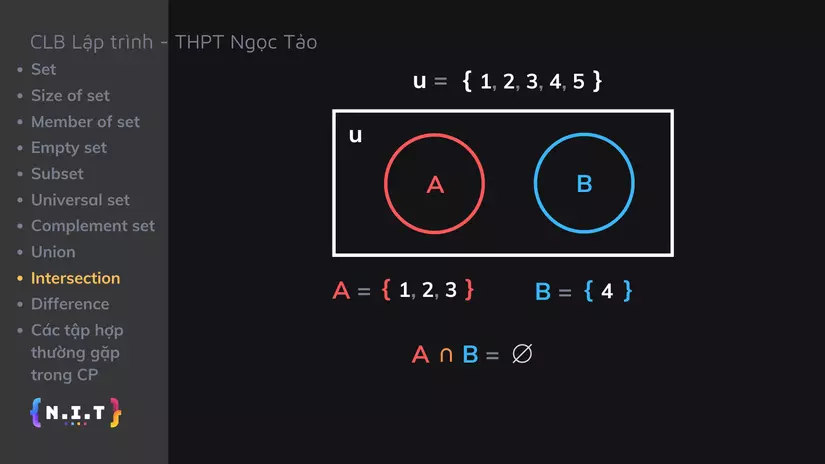
    thì khi đó A ∩ B = ∅

    và A ∪ B = {1, 2, 3, 4}, tức là ta sẽ tô màu cả 2 hình tròn biểu diễn cho A và B ở đây: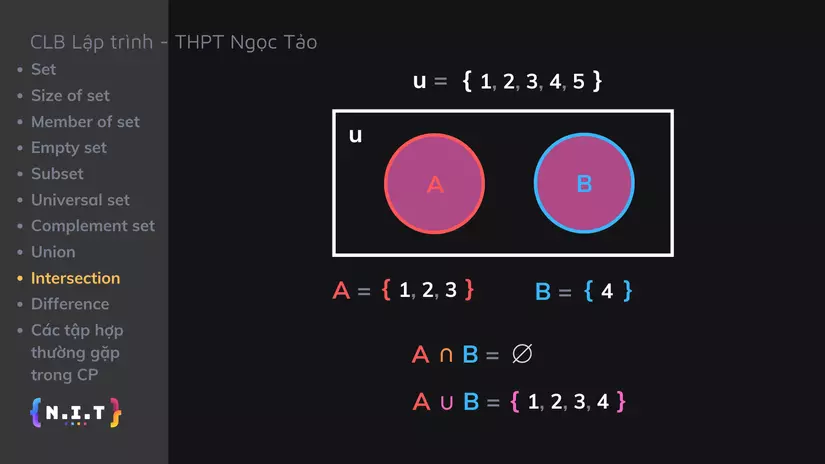

    

Difference

• Khái niệm cuối cùng mình muốn nhắc đến với các bạn đó là difference.

• Chúng ta hay dịch từ difference trong tiếng Anh nghĩa là sự khác biệt.

• Hiểu đơn giản đó là những phần tử xuất hiện trong tập hợp A, mà không xuất hiện trong tập hợp B.

• Trong môn Toán rời rạc mình thấy các thầy gọi là Phép hiệu.

  • Thực ra trong tiếng Anh difference cũng có nghĩa là hiệu số, chính là giá trị mà chúng ta nhận được trong phép trừ đó.

  • Vậy nên cách gọi trong môn Toán rời rạc này cũng hợp lý nhỉ.

• Để ký hiệu cho difference thì chúng ta cũng có 2 cách:

  • Cách 1: A - B

  • Cách 2: A \ B

• Ví dụ: Chúng ta có 1 universal set là:

  u = { 1, 2, 3, 4, 5 }
  

• Bên trong nó chúng ta có 2 tập con là A = {1, 2, 3} và B = {2, 3, 4}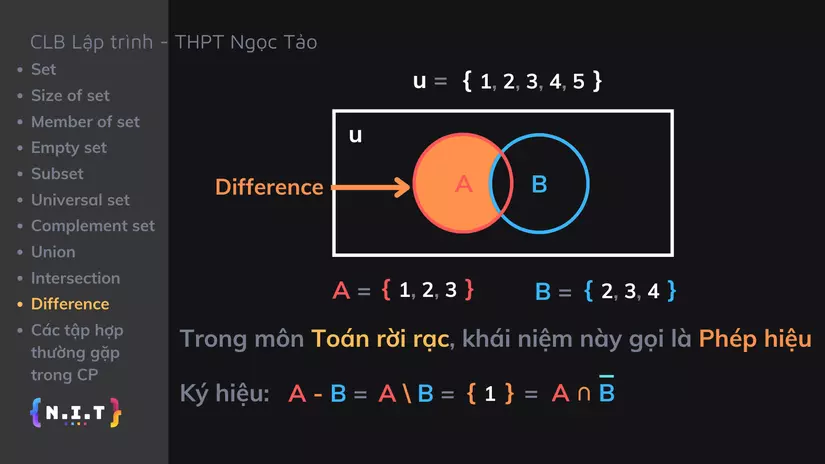

  

• Suy ra, A \ B = {1}, chính là phần màu cam ở trên hình, tức là: những phần tử xuất hiện trong tập hợp A, mà không xuất hiện trong tập hợp B.

Các tập hợp thường dùng trong Lập trình thi đấu

• Các tập hợp mà chúng ta thường thấy trong môn Toán, cũng như xuất hiện rất nhiều trong các bài thi lập trình thi đấu đó là:

  • Tập hợp N, tức là tập hợp số tự nhiên, hay tiếng Anh là natural numbers.

  • Tập hợp Z, tức là tập hợp số nguyên, hay tiếng Anh là integers.

  • Tập hợp Q, tức là tập hợp số hữu tỉ, hay tiếng Anh là rational numbers.

  • Tập hợp R, tức là tập hợp số thực, hay tiếng Anh là real numbers.

Kết luận

• Hi vọng qua bài viết này, các bạn sẽ có thể ôn lại được những kiến thức nền tảng quan trọng về lý thuyết tập hợp (set theory), và đặc biệt là biết được thêm các thuật ngữ chuyên ngành bằng tiếng Anh của chúng.

• Để sau này nếu chúng ta có đọc các đề bài lập trình thi đấu trên các trang web tiếng Anh như Codeforces, Topcoder, ..., thì cũng có thể dễ dàng hiểu ý nghĩa của đề bài.

Hi vọng kiến thức này hữu ích với bạn. Hẹn gặp lại 👋