1. Các luật suy diễn trong thuật toán Vương Hạo

Luật 1: Chuyển vế các giả thuyết và kết luận ở dạng phủ định

Ví dụ: p v q, !(r ^ s), !q, p v r -> s, !p <=> p v q, p v r, p -> s, r ^ s, q

Luật 2: Thay dấu ^ thành dấu phẩy của giả thuyết

Ví dụ: p ^ q, r ^ (!p v s) -> !q v !r <=> p, q, r, !p v s -> !q v !r

Luật 3: Thay dấu v thành dấu phẩy của kết luận

Ví dụ: p ^ q, r ^ (!p v s) -> !q v !r <=> p ^ q, r ^ (!p v s) -> !q, !r

Luật 4: Tách thành hai danh sách riêng của giả thuyết nếu chứa dấu v

Ví dụ: p, !p v q -> q <=> p, !p -> q và p, q -> q

Luật 5: Tách thành hai danh sách riêng của kết luận nếu chứa dấu ^

Luật 6: Thay đổi dấu -> ở các vế giả thuyết và kết luận về dạng chuẩn CNF và DNF

Ví dụ về chuyển đổi dạng chuẩn CNF: ¬(p→q) ∨ (r→p)

1. Loại bỏ các liên kết →, ↔

¬(¬p ∨ q) ∨ (¬r ∨ p)

2. Sử dụng các phép biến đổi tương đương (vd: luật DeMorgan và phép phủ định 2 lần)

(p ∧ ¬q) ∨ (¬r ∨ p)

3. Sử dụng các luật kết hợp (associative rules) và phân bố (distributive rules)

(p ∨ ¬r ∨ p) ∧ (¬q ∨ ¬r ∨ p) <=> (p ∨ ¬r) ∧ (¬q ∨ ¬r ∨ p)

Luật 7: Thay đổi dấu ⬄ ở các vế giả thuyết và kết luận về dạng chuẩn CNF và DNF

2. Cài đặt thuật toán Vương Hạo

% Automated Theorem Proving
% Wang's Algorithm % Define operators.
:-op(700,xfy,<->).
:-op(700,xfy,->).
:-op(600,xfy,v).
:-op(600,xfy,&).
:-op(500,fy,!). % Main call.
prove([],[]).
prove([L|P],[R|A]):- nl, ansi_format([bold],'Statement: ',[]), write(L), write(' |= '), write(R), nl, nl, ansi_format([bold],'Attempting proof!',[]), nl, nl, wang(L,R), prove(P,A). % Procedure of Wang to prove theorem.
wang(L,R):- rules(L,R,[],0), nl, ansi_format([bold,fg(green)], 'Result: The given theorem is true.',[]), nl, nl; ansi_format([bold, fg(red)],'Proof failed for current step!',[]), nl, nl, ansi_format([bold,fg(red)], 'Result: The given theorem is false.',[]), nl, nl. % Move negations from left to right.
rules(L,R,S,T):- member(!X,L), delete(L,!X,Ld), append(S,[[['*Rule 1L '],[Ld,' |= ',[X|R]],T]],Sa), rules(Ld,[X|R],Sa,T). % Move negations from right to left.
rules(L,R,S,T):- member(!X,R), delete(R,!X,Rd), append(S,[[['*Rule 1R '],[[X|L],' |= ',Rd],T]],Sa), rules([X|L],Rd,Sa,T). % Replace conjunction by commas on the left.
rules(L,R,S,T):- member(X & Y,L), delete(L,X & Y,Ld), append(S,[[['*Rule 2 '],[[X,Y|Ld],' |= ',R],T]],Sa), rules([X,Y|Ld],R,Sa,T). % Replace disjunction by commas on the right.
rules(L,R,S,T):- member(X v Y,R), delete(R,X v Y,Rd), append(S,[[['*Rule 3 '],[L,' |= ',[X,Y|Rd]],T]],Sa), rules(L,[X,Y|Rd],Sa,T). % Branch disjunction on the left.
rules(L,R,S,T):- member(X v Y,L), delete(L,X v Y,Ld), Ta is T + 1, append(S,[[['*Rule 4a - Branch Level ',T],[[X|Ld],' |= ',R],T]],Sa), rules([X|Ld],R,Sa,Ta), Tb is T + 1, append([],[[['*Rule 4b - Branch Level ',T],[[Y|Ld],' |= ',R],T]],Sb), rules([Y|Ld],R,Sb,Tb). % Branch conjunction on the right.
rules(L,R,S,T):- member(X & Y,R), delete(R,X & Y, Rd), append(S,[[['*Rule 5a - Branch Level ',T],[L,' |= ',[X|Rd]],T]],Sa), Ta is T + 1, rules(L,[X|Rd],Sa,Ta), Tb is T + 1, append([],[[['*Rule 5b - Branch Level ',T],[L,' |= ',[Y|Rd]],T]],Sb), rules(L,[Y|Rd],Sb,Tb). % Replace implication on the left.
rules(L,R,S,T):- member(X -> Y,L), delete(L,X -> Y,Ld), append(S,[[['*Rule 6L '],[[!X v Y|Ld],' |= ',R],T]],Sa), rules([!X v Y|Ld],R,Sa,T). % Replace implication on the right.
rules(L,R,S,T):- member(X -> Y,R), delete(R,X -> Y,Rd), append(S,[[['*Rule 6R '],[L,' |= ',[!X v Y|Rd]],T]],Sa), rules(L,[!X v Y|Rd],Sa,T). % Replace equivalence on the left.
rules(L,R,S,T):- member(X <-> Y,L), delete(L,X <-> Y,Ld), append(S,[[['*Rule 7L '],[[(X -> Y) & (Y -> X)|Ld],' |= ',R],T]],Sa), rules([(X -> Y) & (Y -> X)|Ld],R,Sa,T). % Replace equivalence on the right.
rules(L,R,S,T):- member(X <-> Y,R), delete(R,X <-> Y,Rd), append(S,[[['*Rule 7R '],[L,' |= ',[(X -> Y) & (Y -> X)|Rd]],T]],Sa), rules(L,[(X -> Y) & (Y -> X)|Rd],Sa,T). % Finally compare both sides.
rules(L,R,S,T):- append(S,[[['*Tautology? '],[L,' |= ',R], T]],Sa), member(X,L), member(X,R), append(Sa,[[['*True. '],[],T]],Sb), printprove(Sb). % If theorem is true then print prove.
printprove([]).
printprove([[P,Q,T]|S]):- tab(T*5), printlist(P), tab(40 - T*5), printlist(Q), nl, printprove(S). % Helper for printing list recursively.
printlist([]).
printlist([H|T]):- write(H), printlist(T).

3. Demo

Bước 1: Chạy chương trình Prolog

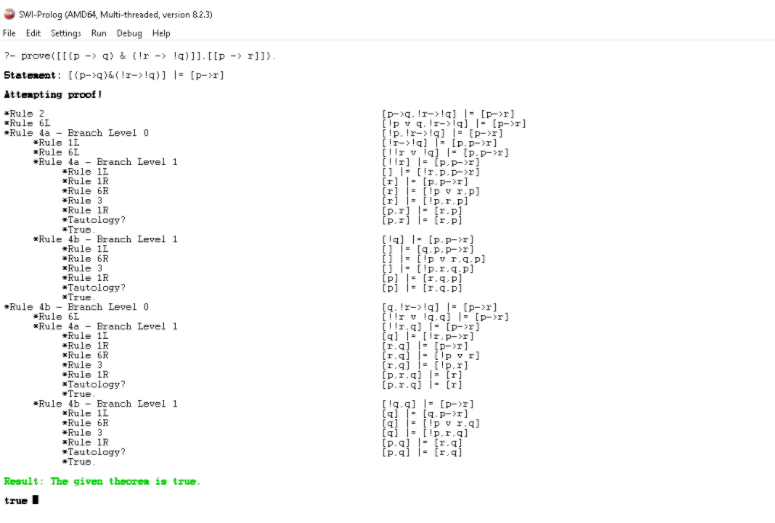
Bước 2: Chứng minh các mệnh đề sau đây

(p -> q) & (!r -> !q) -> (p -> r)

Bước 3: Kết quả