Python: Jump Search

Search là một từ khóa khá là quen thuộc đối với chúng ta. Hiểu theo đúng nghĩa đen của nó chính là "Tìm kiếm". Và có 2 loại chúng ta thường nghe, hoặc làm việc với chúng đó là Binary Search và Linear Search. Nhưng có thể mọi người ít nghe, hoặc chưa từng nghe đến từ khóa Jump Search đúng không nào?
Vậy thì trong bài viết này mình sẽ cùng với các bạn tìm hiểu xem Jump Search là gì và nó hoạt động như thế nào nhé. Let's go!

1. Jump Search

Với Jump Search, các mảng dữ liệu đã được sort được chia thành các phần tử nhỏ được gọi là blocks. Chúng ta sẽ tìm kiếm các search key hay còn gọi là giá trị input bằng cách so sánh các phần tử trong mỗi block. Khi mảng được sắp xếp, vị trí cần tìm là giá trị khớp nhất trong một block.

Khi so sánh search key với các "ứng viên", thuật toán sau đó có thể thực hiện 1 trong 3 điều:

• Nếu "ứng viên" cần tìm nhỏ hơn search key, chúng ta sẽ kiểm tra block tiiếp theo.
• Nếu "ứng viên" cần tìm lớn hơn search key, chúng ta sẽ thực hiện linear search ở chính block hiện tại.
• Nếu "ứng viên" cần tìm giống với search key, lúc đó chúng ta đã tìm được ra "ứng viên" cần tìm rồi.

Kích thước của một block sẽ bằng căn bậc hai của mảng. Do đó các mảng có độ dài là n thì kích thước của 1 khối sẽ là √n, điều này sẽ mang lại cho chúng ta hiệu suất tốt nhất cho hầu hết các mảng.

Nói lý thuyết thì dài dòng, mình sẽ ví dụ ngắn hơn bằng 1 ví dụ nhé.

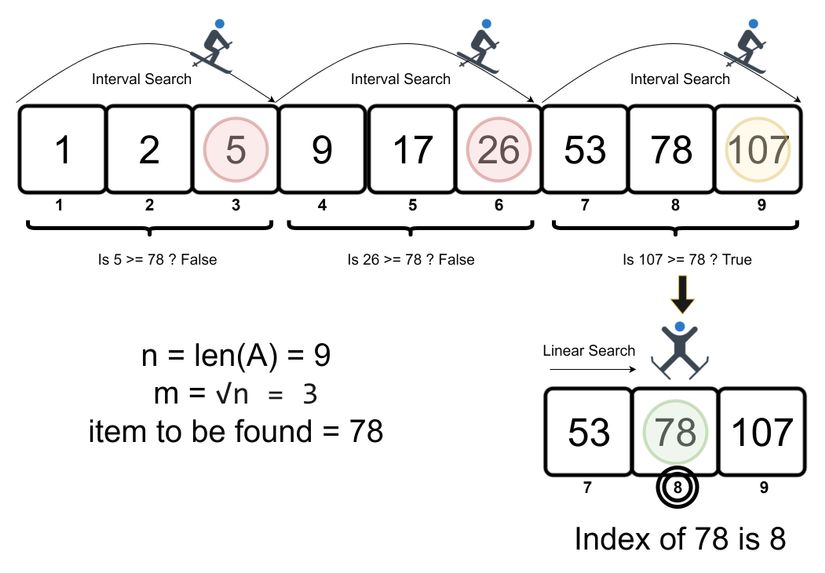
Ở ví dụ này, có 5 bước để tìm kiếm phần tử, trong đó có 2 bước sử dụng Linear Search. Chúng ta đã hình dung ra được cách hoạt động của "nó" rồi đúng không nào. Giờ hãy cùng đi vào chi tiết hơn các bước hoạt động của "nó" nha.

2. Các bước thực hiện Jump Search

Giả sử chúng ta có bài toán:

Input: list A có size là n
Output: Vị trí phù hợp với search key hoặc -1 nếu không tìm thấy.

Các bước thực hiện:

Bước 1 Xác định size của list đã được sort: n = len(A) Bước 2 Xác định size của một block: m = √n Bước 3 Từ vị trí đầu tiên: i = 0, chúng ta lặp lại với mỗi bước là m cho đến khi đến kết thúc. Bước 4 So sánh A[i+m] với item (i+m là vị trí cuối cùng của một block) :

• Nếu A[i+m] == item, thì return i+m và kết thúc.
  
• Nếu A[i+m] > item, thực hiện Linear Search trong một block được gọi là list B = A[i+m]. Tiếp tục lặp lại cho đến khi tìm thấy và return về kết quả phù hợp i nếu tìm thấy rồi sau đó kết thúc.
  
• Nếu A[i+m] < item, tiếp tục bước lặp tiếp theo cho Bước 4.
  Bước 5 Đến khi tìm được i phù hợp thì return và kết thúc. Nếu không tìm thấy kết quả phù hợp nào, trả về -1.

Các bước chỉ có như vậy, giờ chúng ta hãy triển khai nó bằng code Python nha.

3. Implementation

Trước khi thực hiện Jump Search, chúng ta hãy implement function linear_search trước để phục vụ cho bước 4b và 5 nha.

'''
Linear Search function
Arguments:
B - The derived list
item - Element for which the index needs to be found
loc - The Index where the remaining block begins
''' def linear_search(B, item, loc): print("\t Entering Linear Search") i = 0 while i != len(B): if B[i] == item: return loc+i i += 1 return -1

Sau khi có được function linear_search rồi, chúng ta tiếp tục đến "món chính" nào. Function jump_search sẽ nhận 2 tham số là list A và phần tử cần tìm. Hàm math.sqrt() sử dụng để tìm kích thước của block.

'''
Jump Search function
Arguments:
A - The source list
item - Element for which the index needs to be found
'''
import math def jump_search(A, item): print("Entering Jump Search") n = len(A) # Length of the array m = int(math.sqrt(n)) # Step length i = 0 # Starting interval while i != len(A)-1 and A[i] < item: print("Processing Block - {}".format(A[i: i+m])) if A[i+m-1] == item: # Found the search key return i+m-1 elif A[i+m-1] > item: # Linear search for key in block B = A[i: i+m-1] return linear_search(B, item, i) i += m B = A[i:i+m] # Step 5 print("Processing Block - {}".format(B)) return linear_search(B, item, i)

Kết luận

Trong bài viết này, mình chỉ đề cập đến cách hoạt động của Jump Search cũng như cách triển khai chúng trên phương diện code của Python.
Cảm ơn các bạn đã đọc bài. Nếu chưa hài lòng về bài viết, hãy comment phía dưới. Còn nếu bài viết này hữu ích, đừng ngần ngại cho mình xin 1 upvote để lấy động lực viết những bài tiếp theo nha.

Thank you!

Related links:

• https://viblo.asia/p/python-implement-binary-tree-6J3ZgN6AKmB
• https://medium.com/programminginpython-com/python-program-to-implement-linear-search-algorithm-8655a6e11184