Trong phần 2, mình có đề cập đến cấp độ Node trong bài toán Machine Learning in Graphs rồi (mọi người có thể xem lại tại link này: P2. Machine Learning with Graphs). Hôm nay thì viết tiếp những mục còn thiếu ở cái phần 2 đó thôi. Trong đó, mình sẽ giới thiệu một số bài toán Machine Learning ở cấp độ Link/Edges nhé. Let's go.

(Nếu thế thì coi đây là phần 2 của phần 2 nhỉ 🧐🧐🧐)

b. Cấp độ Link/Edges

Link Prediction là ví dụ điển hình cho bài toán Machine Learning with Graphs ở cấp độ Link/Edges. Nghe tên thì mình nghĩ mọi người cũng sẽ hiểu bài toán này làm gì rồi nhỉ. Link Prediction là một ứng dụng quan trọng và cũng thường được ứng dụng phổ biến trong đời sống. Bằng cách dự đoán các Link có thể có trong một Graph, một số ứng dụng của bài toán này có thể kể đến bao gồm friend recommendation trên các trang mạng xã hội (cái này thì quá quen thuộc nếu ai có dùng Facebook rồi nhé), protein interaction prediction trong các phản ứng hoá học, v.v.

Một số cách thường được sử dụng để thực hiện bài toán này bao gồm:

• Phương pháp Heuristic: Phương pháp này tập trung chủ yếu vào việc tính toán sự giống nhau giữa 2 node một cách heuristic (ví dụ như node degree, common neighbors (lân cận chung), v.v.) để dự đoán xác suất có 1 link giữa hai node này. Cách này thì sẽ dựa chủ yếu vào các đặc trưng về mặt cấu trúc của node thay vì đi sâu vào các đặc trưng về nội dung của node.
• Phương pháp Latent-feature: Ý tưởng của phương pháp này thì lại giống với ý tưởng của bài toán Embedding (hay gần gũi hơn là Matrix Factorization), tức là, ta cũng sẽ tính toán sự giống nhau giữa các node nhưng trước đó thì sẽ phân rã ma trận biểu diễn Graph về một chiều không gian có số chiều nhỏ hơn để dễ tính toán hơn. Phương pháp này thì sẽ đi sâu hơn vào việc chọn lọc đặc trưng về nội dung của node để so sánh sự giống nhau, từ đó sẽ dự đoán có kết nối giữa hai node này hay không.
• Phương pháp Content-based: Phương pháp này thay vì tập trung vào đặc trưng của node thì dựa vào cấu trúc của Graph để dự đoán liên kết có thể có giữa 2 node.

Trong mục này thì mình sẽ đề cập đến các cách phổ biến trong phương pháp Heuristic nhé, các phương pháp còn lại, khi nào mình viết tới phần Graph Neural Network thì mình sẽ đề cập nhé (chưa biết khi nào thôi 🤣). Mình sẽ đề cập đến 2 cách:

• Local neighborhood overlap (tạm dịch: lấy đặc trưng dựa vào chồng lấn cục bộ), hay còn gọi là Local Heuristics
• Global neighborhood overlap (tạm dịch: lấy đặc trưng dựa vào chồng lấn toàn cục), hay còn gọi là Global Heuristics

Okay, đi sâu vào từng vấn đề nhé:

1. Local Heuristics:

Gọi là Local Neighborhood/Heuristics vì ở đây ta sẽ xem xét vùng lân cận của 2 node mà chúng ta muốn dự đoán xem có xuất hiện Link/Edge hay không mà không cần quan tâm quá nhiều đến toàn bộ cấu trúc Graph. Ý tưởng ở đây giống như việc bạn A và bạn B có nhiều bạn chung trên Facebook, thế nên Facebook sẽ đưa ra gợi ý kết bạn cho cả 2 đấy. Một số ví dụ điển hình cho phương pháp này gồm:

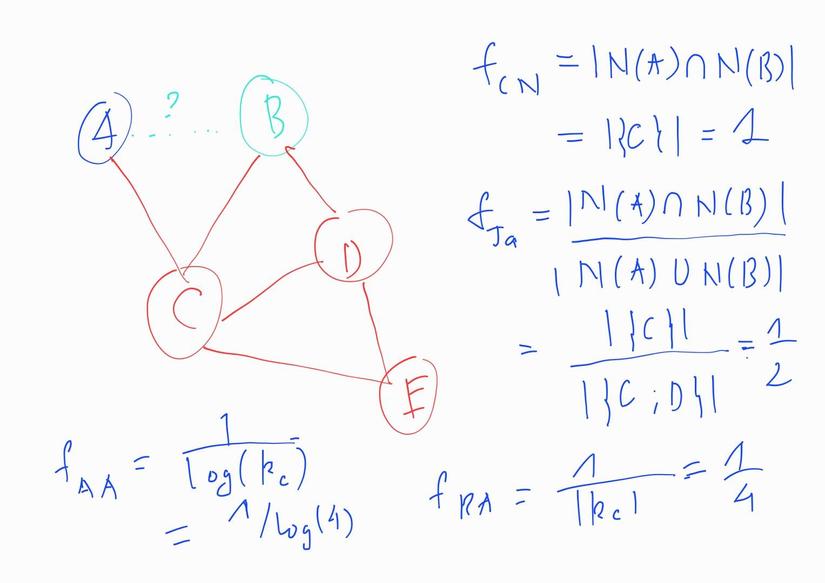
• Common Neighbors (CN): đếm số node chung mà 2 node có liên kết.

$$f_{CN}(A, B) = |N(A) \cap N(B)|$$

• Jaccard Score: đo tỉ lệ giữa số node chung của 2 node và tổng số node mà 2 node có liên kết:

$$f_{Jaccard}(A, B) = \frac{|N(A) \cap N(B)|}{|N(A) \cup N(B)|}$$

• Preferential Attachment (PA): Phương pháp này sẽ giả định node A sẽ tồn tại một liên kết với node B nếu node B có chỉ số node degree lớn (nói nôm na vui vui là "Thấy người sang bắt quàng làm họ" đấy 😂):

$$f_{PA} =|N(A)| * |N(B)|$$

• Adamin-Adar (AA): Phương pháp này lại giả định là: Node có chỉ số Node Degree càng cao thì một node mới càng khó tồn tại 1 cạnh nối tới cái node này (kiểu như: "Tui không có nhu cầu thêm bạn mới" vậy đó). Phương pháp này còn có một biến thể khác, đó là Resource allocation (RA)

$$f_{AA} = \sum_{u \in N(A) \cap N(B)} \frac{1}{log(|k_u|)}$$

$$f_{RA} = \sum_{u \in N(A) \cap N(B)} \frac{1}{|k_u|}$$

Ví dụ một graph đơn giản nhé:

2. Global Heuristic

Nhược điểm của Local Heuristic là: nếu như 2 node A và B không có bất kì node chung nào trong vùng lân cận của mình thì sẽ khó mà dự đoán được liệu node A và node B đó có tồn tại một Link/Edge giữa chúng hay không. Chúng ta nhìn vào công thức của Common Neighbors và Jaccard Score sẽ thấy điều này (luôn bằng 0).

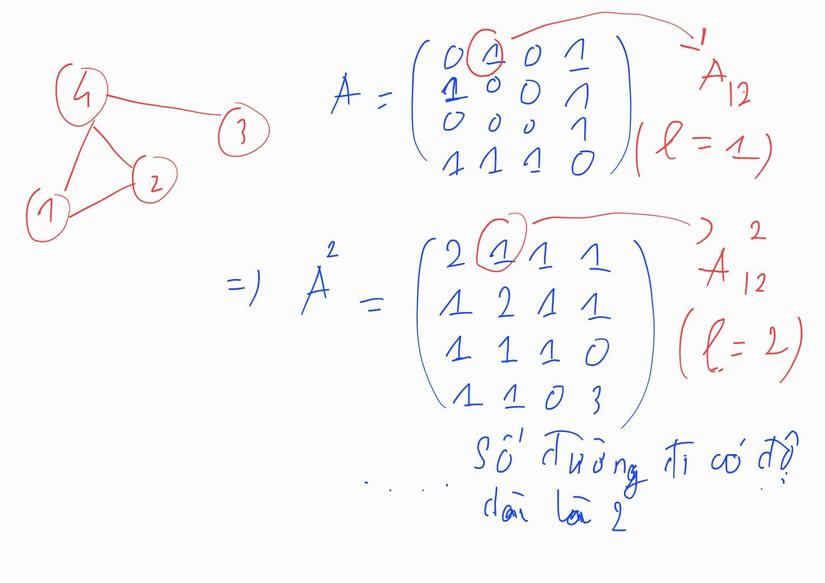
Từ đó, Global Neighborhood/Heuristics được đề xuất nhằm giải quyết nhược điểm này. Ví dụ điển hình cho phương pháp này là Katz Index. Katz Index sẽ đếm số lượng path giữa 2 node với bất kì độ dài nào để đánh giá xem giữa 2 node đó có thể có kết nối nào hay không.

Theo đó, công thức của Katz Index sẽ là:

$$S_{v_1, v_2} = \sum_{l=1}^{\infty}\beta^l|A^l_{{v_1}{v_2}}|$$

Với $\beta$ là một hằng số nằm trong khoảng $[0, 1]$, $A^l_{{v_1}{v_2}}$ ($A$ mũ $l$ nhé) là số đường đi có chiều dài là $l$ từ node $v_1$ tới node $v_2$ (với $A$ là Adjacency Matrix bậc 1, nên $A_{{v_1}{v_2}}$ là giá trị của phần tử có toạ độ $(v_1, v_2)$ trong $A$). Vậy Katz Index có thể được hiểu là "Sum over all walks lengths giữa 2 node $v_1$ và $v_2$).

Khi đó ma trận Katz sẽ có dạng:

$$S = \sum_{i=1}^{\infty}\beta^{i}A^i$$

Ví dụ:

3. Tạm kết

Thực ra khi viết tới đây thì mình định viết thêm về Cấp độ Graph trong các bài toán Machine Learning truyền thống. Nhưng mình nghĩ lại rồi 🤣 mình sẽ viết đến phần Graph Neural Network rồi sẽ đề cập đến mục này luôn (vì căn bản là kỹ thuật chuyển Graph về Kernel cũng là một kỹ thuật khá giống với cách tiếp cận của Graph Neural Network), nên để sau nhé.

Tổng kết lại thì trong 2 phần, là phần 2: Machine Learning with Graphs và phần này thì mình đã đề cập đến các cách tiếp cận Machine Learning truyền thống trong Homogeneous Graph. Tuy nhiên thì Graph thực tế sẽ phức tạp hơn rất nhiều (Knowledge Graph) nên các cách tiếp cận theo hướng này đôi khi sẽ không hiệu quả. Chính vì vậy, các kỹ thuật Deep Learning hiện đại hơn đã ra đời để giải quyết các Graph phức tạp hơn. Hẹn gặp lại mọi người trong những phần tiếp theo nhé.

Tài liệu tham khảo:

CS224W: Machine Learning with Graphs

Graph Neural Networks: Link Prediction