1. Introduction

Đối với các bạn học deep learning thì không thể không biết tới RNN, một thuật toán cực kì quan trọng chuyên xử lý thông tin dạng chuỗi. Đầu tiên, hãy nhìn xem RNN có thể làm gì. Dưới đây là một vài ví dụ.

• Machine Translation (Dịch máy)
• Mô hình hóa ngôn ngữ và sinh văn bản: đây có lẽ là khả năng ấn tượng nhất đối với mình.
• Nhận dạng giọng nói
• Mô tả hình ảnh: RNN kết hợp cùng CNN để sinh ra mô tả cho hình ảnh chưa được gán nhãn. Đây cũng là một bài tập khá hay mà mình sẽ giới thiệu trong bài viết tiếp theo.

Vậy, làm sao RNN làm được những việc này? Hi vọng thông qua bài viết này mình có thể cung cấp một cái nhìn rõ ràng và dễ hiêủ về RNN.

Let's go !!!

2. Recurrent Neural Network

Ý tưởng căn bản

Một cách nôm na, đối với mạng neural thông thường, chúng ta cho tất cả dữ liệu vào cùng một lúc. Nhưng đôi khi, dữ liệu của chúng ta mang ý nghĩa trình tự, tức nếu thay đổi trình tự dữ liệu, kết quả sẽ khác.

Dễ thấy rõ nhất ở dữ liệu văn bản. Ví dụ, “Con ăn cơm chưa” và “Con chưa ăn cơm”, nếu tách mỗi câu theo từ, ta được bộ vocab [ ‘con’, ‘ăn’, ‘cơm’, ‘chưa’], one hot encoding và cho tất cả vào mạng neural , có thể thấy ngay, không có sự phân biệt nào giữa 2 câu trên. Việc đảo thứ tự duyệt các từ làm sai lệch ý nghĩ của câu.

Nói cách khác, chúng ta cần một mạng neural có thể xử lí tuần tự.

Vậy làm sao để xử lí tuần tự, đầu tiên cần đưa đầu vào vào một cách tuần tự.

Mình là kiểu người hiểu nhanh hơn thông qua hình ảnh , và mình nghĩ đây là hình ảnh thể hiện rõ ràng nhất rốt cuộc RNN làm gì. Mỗi block RNN sẽ lấy thông tin từ các block trước và input hiện tại.

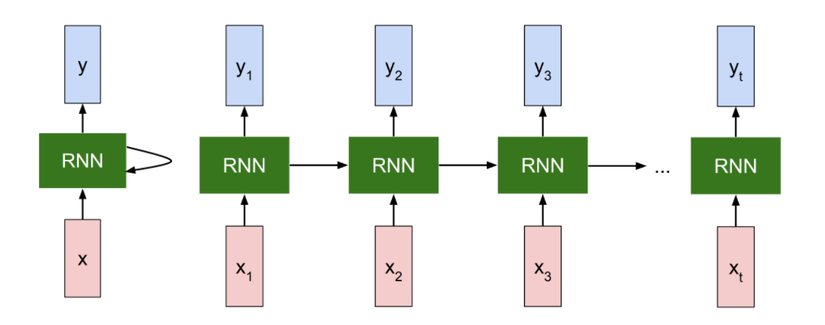
Các x ở đây đại diện cho dữ liệu đầu vào lần lượt (được chia theo time step).

$x_{t}$ đại diện cho time step thứ t, và $y_{t}$ là output của một step. Ví dụ, $x_{2}$ sẽ là vector đại diện của từ thứ 2 trong câu văn bản.

Hình ảnh dưới đây cho thấy rõ hơn điều gì thực sự xảy ra trong một step.

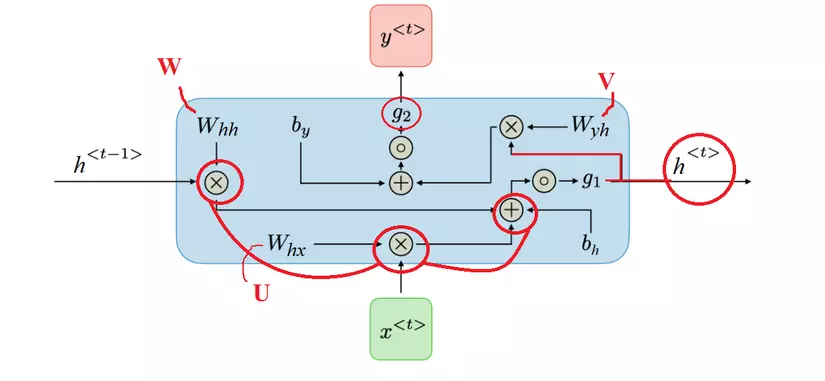
Trong đó, g1, g2 là các activation function. g1 thường là sigmoid, tanh, ReLu và vân vân, trong khi g2 thường là softmax.

• Hidden state $h_{t}$ (trong một số tài liệu tường ký hiện $s_{t}$). Đây chính là bộ nhớ của mạng. $h_{t}$ là tổng hợp thông tin của hidden state trước ( $h_{t-1}$) cộng với input tại time step t ( $x_{t}$). Activation function ở đây chủ yếu là tanh hoặc ReLu.

$h_{t} = g1 ( W_{hh} * h_{t-1} + W_{hx} * x_{t} + b_{h} )$

Hoặc có thể viết gọn hơn:

$h_{t} = g1 ( ( W_{hh} W_{hx}) ( \begin{matrix} h_{t-1} \\ x_{t} \end{matrix}))$

$h_{t} = g1 ( ( W) ( \begin{matrix} h_{t-1} \\ x_{t} \end{matrix}))$

• Output của từng time step $y_{t}$ :

$y_{t} = g2 ( W_{yh} * h_{t} + b_{y} )$

Rất đơn giản và cơ bản. Một step của RNN có thể được triển khai bằng code numpy như sau:

def rnn_step_forward(x, prev_h, Wx, Wh, b): """ The input data has dimension D, the hidden state has dimension H, and the minibatch is of size N. Inputs: - x: Input data for this timestep, of shape (N, D) - prev_h: Hidden state from previous timestep, of shape (N, H) - Wx (Whx): Weight matrix for input-to-hidden connections, of shape (D, H) - Wh (Whh): Weight matrix for hidden-to-hidden connections, of shape (H, H) - b: Biases of shape (H,) Returns a tuple of: - next_h: Next hidden state, of shape (N, H) - cache: Tuple of values needed for the backward pass. """ next_h, cache = None, None next_h = np.tanh(x @ Wx + prev_h @ Wh + b) # N x H cache = (x, prev_h, Wx, Wh, next_h) return next_h, cache

Tính toán lan truyền ngược. (BPTT - Backpropagation Through Time)

Như vậy, trong quá trình training, có 3 tham số chúng ta cần tìm là $W_{hh},W_{hx}, W_{yh}$. Chúng ta cần tính $\frac{ \partial L}{ \partial W_{hx}} ,\frac{ \partial L}{ \partial W_{hh} } \frac{ \partial L}{ \partial W_{hy}}$. (với $L$ là loss function)

(Do quá lười type công thức) Các bạn có thể tham khảo phần tính đạo hàm đầy đủ dùng chain rule trong bài viết này của anh Tuan Nguyen (hoặc nhiều toán hơn nữa ở đây).

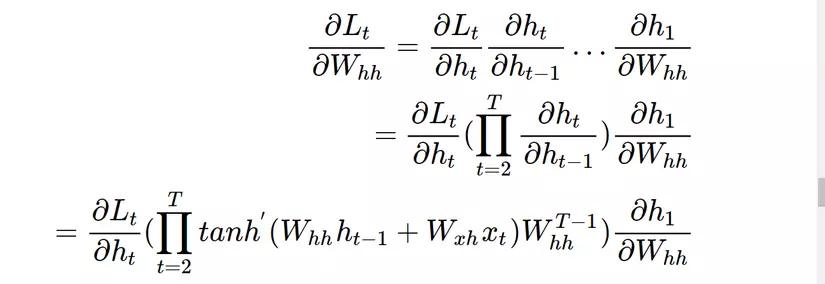
Nhìn chung, ta có thể thấy vấn đề cơ bản ở đây là:

Trong mạng NN truyền thống, ta không chia sẻ tham số giữa các tầng mạng. Tuy vậy, với RNN, ta có thể thấy, để tính đạo hàm của loss theo $W_{hh}$, ta phụ thuộc vào $h_{t-1}$, mà $h_{t-1}$ lại phụ thuộc vào $h_{t-2}$ và $x_{t-1}$. Nói nôm na, ta phải cộng tất cả đầu ra ở các bước trước để tính đạo hàm. Điều này gây ra một hạn chế lớn cho RNN.

def rnn_step_backward(dnext_h, cache): """Backward pass for a single timestep. Inputs: - dnext_h: Gradient of loss with respect to next hidden state, of shape (N, H) - cache: Cache object from the forward pass Returns a tuple of: - dx: Gradients of input data, of shape (N, D) - dprev_h: Gradients of previous hidden state, of shape (N, H) - dWhx: Gradients of input-to-hidden weights, of shape (D, H) - dWhh: Gradients of hidden-to-hidden weights, of shape (H, H) - db: Gradients of bias vector, of shape (H,) """ dx, dprev_h, dWhx, dWhh, db = None, None, None, None, None x, prev_h, Whx, Whh, next_h = cache d_tanh = dnext_h*(1.0 - next_h**2) # N x H dx = d_tanh.dot(Whx.T) # N x D dprev_h = d_tanh.dot(Whh.T) # N x H dWhx = x.T.dot(d_tanh) # D x H dWhh = prev_h.T.dot(d_tanh) # H x H db = np.sum(d_tanh, axis=0) # 1 x H return dx, dprev_h, dWhx, dWhh, db

Implement code RNN sử dụng thư viện hỗ trợ PyTorch:

import torch
from torch import nn
class Model(nn.Module): def __init__(self, input_dim, output_dim, hidden_dim, n_layers): super(Model, self).__init__() self.hidden_dim = hidden_dim self.n_layers = n_layers # RNN Layer self.rnn = nn.RNN(input_dim, hidden_dim, n_layers, batch_first=True) # Fully connected layer self.fc = nn.Linear(hidden_dim, output_dim) def forward(self, x): batch_size = x.size(0) # Initializing hidden state for first input using method defined below hidden = self.init_hidden(batch_size) # Passing in the input and hidden state into the model and obtaining outputs out, hidden = self.rnn(x, hidden) # Reshaping the outputs -> fit into the fully connected layer out = out.contiguous().view(-1, self.hidden_dim) out = self.fc(out) return out, hidden def init_hidden(self, batch_size): # Generates the first hidden state of zeros in forward hidden = torch.zeros(self.n_layers, batch_size, self.hidden_dim) return hidden

Implement code sử dụng thư viện TensorFlow:

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers model = keras.Sequential()
model.add(layers.Embedding(input_dim=input_dim, output_dim=output_dim)) # Add a LSTM layer with 128 internal units.
model.add(layers.RNN(128)) # Add a Dense layer with 10 units. (10 classes)
model.add(layers.Dense(10)) model.summary()

Như vậy, so với mạng NN bình thường, RNN có thể nắm bắt thông tin dạng chuỗi. Điều này cũng góp phần giúp RNN có thể đáp ứng chuỗi đầu vào có độ dài tùy ý, kích thước model không bị phụ thuộc vào size đầu vào.

Hạn chế của RNN là gì?

• Phải thực hiện tuần tự: Không tận dụng được khả năng tính toán song song của máy tính (GPU/TPU).

• Vanishing gradient (Đạo hàm bị triệt tiêu)

  Vì hàm kích hoạt (tanh hay sigmoid) của ta sẽ cho kết quả đầu ra nằm trong đoạn $[-1, 1]$ (với sigmoid là $[0, 1]$) nên đạo hàm của nó sẽ bị đóng trong khoảng $[0, 1]$ (với sigmoid là $[0, 0.25]$).

  Ở trên, chúng ta đã dùng chain rule để tính đạo hàm. Có một vấn đề ở đây là, hàm tanh lẫn sigmoid đều có đạo hàm bằng 0 tại 2 đầu. Mà khi đạo hàm bằng 0 thì nút mạng tương ứng tại đó sẽ bị bão hòa. Lúc đó các nút phía trước cũng sẽ bị bão hoà theo. Nên với các giá trị nhỏ trong ma trận, khi ta thực hiện phép nhân ma trận sẽ đạo hàm tương ứng sẽ xảy ra Vanishing gradient, tức đạo hàm bị triệt tiêu chỉ sau vài bước nhân. Như vậy, các bước ở xa sẽ không còn tác dụng với nút hiện tại nữa, làm cho RNN không thể học được các phụ thuộc xa. Vấn đề này không chỉ xảy ra với mạng RNN mà ngay cả mạng neural truyền thống với nhiều lớp cũng có hiện tượng này.

  Với cách nhìn như trên, ngoài Vanishing gradient, ta còn gặp phải Exploding Gradient (bùng nổ đạo hàm). Tùy thuộc vào hàm kích hoạt và tham số của mạng, vấn đề này xảy ra khi các giá trị của ma trận là lớn (lớn hơn 1). Tuy nhiên, người ta thường nói về vấn đề Vanishing nhiều hơn là Exploding, vì 2 lý do sau.

  Thứ nhất, bùng nổ đạo hàm có thể theo dõi được vì khi đạo hàm bị bùng nổ thì ta sẽ thu được kết quả là một giá trị phi số NaN làm cho chương trình của ta bị dừng hoạt động.

  Thứ hai, bùng nổ đạo hàm có thể ngăn chặn được khi ta đặt một ngưỡng giá trị trên (tham khảo kỹ thuật Gradient Clipping). Còn rất khó để theo dõi sự mất mát đạo hàm cũng như tìm cách xử lí nó.

Để xử lý Vanishing Gradient, có 2 cách phổ biến:

• Cách thứ nhất, thay vì sử dụng activation function là tanh và sigmoid, ta thay bằng ReLu (hoặc các biến thể như Leaky ReLu). Đạo hàm của ReLu hoặc là 0 hoặc là 1, nên ta có thể kiểm soát phần nào vấn đề mất mát đạo hàm.

• Cách thứ hai, ta thấy RNN thuần không hề có thiết kế nào để lọc đi những thông tin không cần thiết. Ta cần thiết kế một kiến trúc có thể nhớ dài hạn hơn, đó là LSTM và GRU.

3. LSTM (Long Short-term memory)

Mình nghĩ hình ảnh sau đây là rõ nét nhất để so sánh giữa RNN và LSTM.

RNN

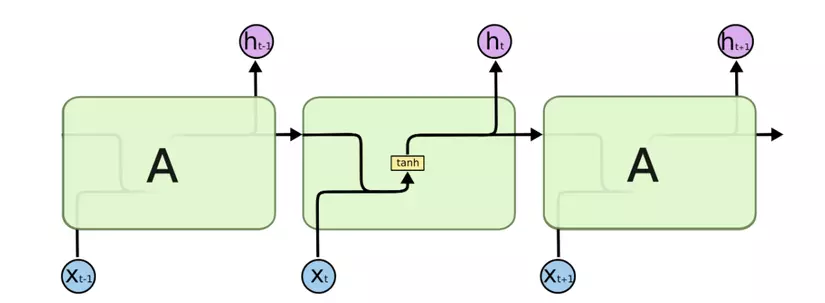Hình 3.1

LSTM

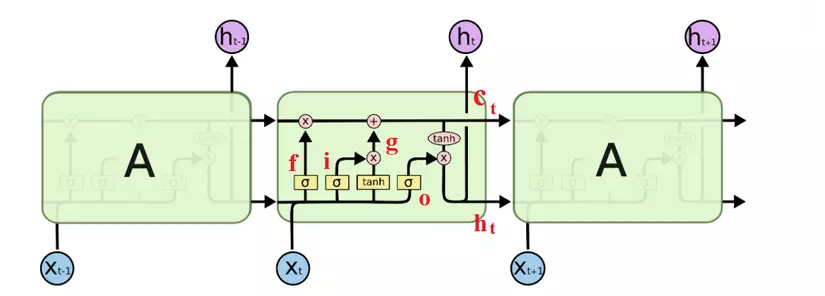Hình 3.2

Về cơ bản, ý tưởng không khác nhau là mấy. Chúng ta chỉ thêm một số tính toán ở đây. Tất cả được tóm tắt trong hình sau.

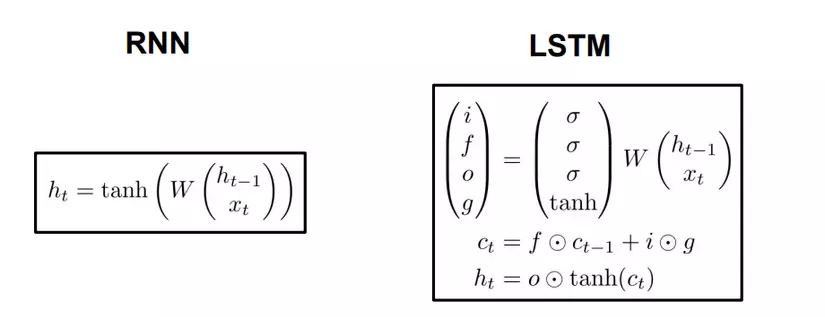
Đầu tiên, chúng ta có $i, f, g$ có công thức gần giống hệt nhau và chỉ khác mỗi ma trận tham số. Chính ma trận này sẽ quyết định chức năng khác nhau của từng cổng. $\sigma$ là ký hiệu của hàm sigmoid. Quan sát hình 3.2 để thấy rõ hơn vị trí các cổng:

• Input gate $i$ - cổng vào.

  Cổng vào giúp quyết định bao nhiêu lượng thông tin đầu vào sẽ ảnh hưởng đến trạng thái mới. Quyết định bằng cách nào, thông qua đặc điểm của hàm sigmoid (đầu ra nằm trong khoảng $[0,1]$), như vậy khi một vector thông tin đi qua đây, nếu nhân với 0, vector sẽ bị triệt tiêu hoàn toàn. Nếu nhân với 1, hầu hết thông tin sẽ được giữ lại.

• Tương tự như vậy, $f$ là forget gate - cổng quên.

  Cổng quyết định sẽ bỏ đi bao nhiêu lượng thông tin đến từ trạng thái trước đó.

• Cuối cùng, cổng $o$ là output gate - cổng ra.

  Cổng điều chỉnh lượng thông tin có thể ra ngoài $y_{t}$ và lượng thông tin truyền tới trạng thái tiếp theo.

• Tiếp theo, g thực chất cũng chỉ là một trạng thái ẩn được tính dựa trên đầu vào hiện tại $x_{t}$ và trạng thái trước $h_{t-1}$. Tính hoàn toàn tương tự như input gate, chỉ thay vì dùng sigmoid, ta dùng tanh. Kết hợp hai điều này lại để cập nhật trạng thái mới.

• Cuối cùng, ta có $c_{t}$ là bộ nhớ trong của LSTM. Nhìn vào công thức, có thể thấy nó là tổng hợp của bộ nhớ trước $c_{t-1}$ đã được lọc qua cổng quên f, cộng với trạng thái ẩn g đã được lọc bởi cổng vào i. Cell state sẽ mang thông tin nào quan trọng truyền đi xa hơn và sẽ được dùng khi cần. Đây chính là long term memory.

• Sau khi có $c_{t}$, ta sẽ đưa nó qua cổng ra để lọc thông tin một lần nữa, thu được trạng thái mới $h_{t}$.

Nếu nhìn kỹ một chút, ta có thể thấy RNN truyền thống là dạng đặc biệt của LSTM. Nếu thay giá trị đầu ra của input gate là 1 và đầu ra forget gate là 0 (không nhớ trạng thái trước), ta được RNN thuần.

def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b): """ Forward pass for a single timestep of an LSTM. The input data has dimension D, the hidden state has dimension H, and we use a minibatch size of N. Inputs: - x: Input data, of shape (N, D) - prev_h: Previous hidden state, of shape (N, H) - prev_c: previous cell state, of shape (N, H) - Wx: Input-to-hidden weights, of shape (D, 4H) - Wh: Hidden-to-hidden weights, of shape (H, 4H) - b: Biases, of shape (4H,) Returns a tuple of: - next_h: Next hidden state, of shape (N, H) - next_c: Next cell state, of shape (N, H) - cache: Tuple of values needed for backward pass. """ next_h, next_c, cache = None, None, None H = b.shape[0] // 4 a = x.dot(Wx) + prev_h.dot(Wh) + b i = sigmoid(a[:, :H]) f = sigmoid(a[:, H:2*H]) o = sigmoid(a[:, 2*H:3*H]) g = np.tanh(a[:, 3*H:4*H]) next_c = f*prev_c + i*g next_h = o * np.tanh(next_c) cache = (x, Wx, prev_h, Wh, b, a, prev_c, i, f, o, g, next_c, next_h) return next_h, next_c, cache

Tổng kết

Nhìn một lượt qua kiến trúc LSTM, ta có thể tóm tắt:

• Thứ nhất, LSTM có long-term memory. Tuy nhiên, $h_{t}, g_{t}$ khá giống với RNN truyền thống, tức có short-term memory. Nhìn chung, LSTM giải quyết phần nào vanishing gradient so với RNN, nhưng chỉ một phần.
• Với lượng tính toán như trên, RNN đã chậm, LSTM nay còn chậm hơn.

Tuy vậy, với những cải tiến so với RNN thuần, LSTM đã và đang được sử dụng phổ biến. Trên thực tế, cách cài đặt LSTM cũng rất đa dạng và linh hoạt theo bài toán, tuy nhiên vẫn dựa trên LSTM chuẩn như trên.

4. Reference

• RNN cheatsheet của cs231n:

  https://stanford.edu/~shervine/teaching/cs-230/cheatsheet-recurrent-neural-networks#architecture

• Phần code được tham khảo từ Assignment 3 của cs231n.

  https://cs231n.github.io/

• Nếu bạn muốn đọc rõ hơn về các công thức LSTM:

  https://colah.github.io/posts/2015-08-Understanding-LSTMs/

  Phiên bản tiếng Việt của nó ở đây:

  https://dominhhai.github.io/vi/2017/10/what-is-lstm/#3-2-bên-trong-lstm

• Một số phương pháp kiểm soát Vanishing Gradient:

  https://viblo.asia/p/ORNZqPEeK0n