Thay đổi quan niệm về thuật toán qua vài bài code thiếu nhi

Một quan niệm sai lầm phổ biến là luyện thuật toán đồng nghĩa với học thuộc nhiều thuật toán. Điều này dẫn đến luyện tập không hiệu quả, chán ghét, chối bỏ thuật toán, v.v. Để cho bạn yêu lại từ đầu với thuật toán, sau đây là một vài bài code thiếu nhi không yêu cầu hiểu biết nhiều về thuật toán, ai cũng có thể làm được, nhưng lại phản ánh một khía cạnh quan trọng hay bị bỏ qua trong thuật toán.

Mỗi bài đều có link để bạn submit code và xem kết quả. Bạn phải tự làm trước khi đọc solution, nếu không nhúng tay vào làm sẽ không học được gì cả. Hoặc cũng có thể bạn nghĩ nó dễ òm, mà lại làm sai đấy. 🤭

Solution viết bằng Python, nếu bạn không biết Python cũng không sao, chủ yếu bạn hiểu ý tưởng là có thể tự code lại được. Hoặc bạn có thể nhờ ChatGPT chuyển code sang ngôn ngữ bạn biết.

Leetcode 1688: Count of Matches in Tournament

Problem

Link: https://leetcode.com/problems/count-of-matches-in-tournament/description/.

Bạn được cho một số nguyên n, số đội trong một giải đấu có quy tắc kỳ lạ:

• Nếu số đội hiện tại là số chẵn, mỗi đội sẽ được ghép cặp với một đội khác. Tổng số trận đấu là n / 2 và n / 2 đội sẽ tiến vào vòng tiếp theo.
• Nếu số đội hiện tại là số lẻ, một đội sẽ được chọn ngẫu nhiên để tiến vào giải đấu, và các đội còn lại sẽ được ghép cặp. Tổng số trận đấu là (n - 1) / 2 và (n - 1) / 2 + 1 đội sẽ tiến vào vòng tiếp theo.

Hãy trả về tổng số trận đấu đã diễn ra trong giải đấu cho đến khi có người chiến thắng được xác định.

Ví dụ 1:

• Input: n = 7

• Output: 6

• Giải thích: Chi tiết của giải đấu:

  1. Vòng 1: Số đội = 7, Số trận đấu = 3, và 4 đội tiến vào vòng tiếp theo.
  2. Vòng 2: Số đội = 4, Số trận đấu = 2, và 2 đội tiến vào vòng tiếp theo.
  3. Vòng 3: Số đội = 2, Số trận đấu = 1, và 1 đội được tuyên bố là người chiến thắng.

  Tổng số trận đấu = 3 + 2 + 1 = 6.

Ví dụ 2:

• Input: n = 14

• Output: 13

• Giải thích: Chi tiết của giải đấu:

  1. Vòng 1: Số đội = 14, Số trận đấu = 7, và 7 đội tiến vào vòng tiếp theo.
  2. Vòng 2: Số đội = 7, Số trận đấu = 3, và 4 đội tiến vào vòng tiếp theo.
  3. Vòng 3: Số đội = 4, Số trận đấu = 2, và 2 đội tiến vào vòng tiếp theo.
  4. Vòng 4: Số đội = 2, Số trận đấu = 1, và 1 đội được tuyên bố là người chiến thắng.

  Tổng số trận đấu = 7 + 3 + 2 + 1 = 13.

Ràng buộc:

• 1 <= n <= 200

Solution

Nếu bạn đã biết lập trình cơ bản rồi thì bài này đơn giản thôi nhỉ? Mỗi trận đấu 2 đội, nên số trận đấu mỗi vòng là n / 2, nếu số đội lẻ thì thêm 1 đội vào vòng trong. Sau mỗi trận số đội cũng giảm đi một nửa. Lặp lại đến khi chỉ còn 1 đội.

class Solution: def numberOfMatches(self, n: int) -> int: matches = 0 while n > 1: if n % 2 == 0: matches += n // 2 n = n // 2 else: matches += (n - 1) // 2 n = ((n - 1) // 2) + 1 return matches

Tuy nhiên, nếu bài này được hỏi trước khi bạn biết lập trình, có lẽ bạn đã có câu trả lời khác.

Có tất cả n đội, thi đấu đến khi còn 1 đội.

Có n - 1 đội bị loại.

Mỗi trận đấu loại 1 đội.

Nên có n - 1 trận đấu. Duh! 🤷‍♀️

Kết quả đơn giản chỉ là:

class Solution: def numberOfMatches(self, n: int) -> int: return n - 1

Leetcode 1332: Remove Palindromic Subsequences

Problem

Link: https://leetcode.com/problems/remove-palindromic-subsequences/description/.

Bạn được cho một chuỗi s chỉ bao gồm các ký tự 'a' và 'b'. Trong một bước, bạn có thể loại bỏ một dãy con đối xứng khỏi s.

Hãy trả về số bước tối thiểu để làm cho chuỗi cho trước trở nên rỗng.

Một dãy là dãy con của một chuỗi cho trước nếu nó được tạo ra bằng cách xóa một số ký tự của chuỗi cho trước mà không thay đổi thứ tự của chúng. Lưu ý rằng một dãy con không cần phải liên tiếp. Hoặc nói cách khác, dãy con của một chuỗi là dãy gồm các phần tử lấy từ chuỗi giữ nguyên thứ tự. Ví dụ xét chuỗi "abcd":

• "acd" là dãy con.
• "bd" là dãy con.
• "ba" không phải là dãy con.

Một dãy được gọi là đối xứng nếu nó đọc giống nhau từ cả hai chiều, xuôi và ngược. Ví dụ abbcbba đối xứng, abcabc không đối xứng.

Ví dụ 1:

• Input: s = "ababa"
• Output: 1
• Giải thích: s đã là một chuỗi đối xứng, vì vậy toàn bộ có thể bị loại bỏ trong một bước.

Ví dụ 2:

• Input: s = "abb"
• Output: 2
• Giải thích: "abb" -> "bb" -> "". Loại bỏ chuỗi con đối xứng "a" sau đó "bb".

Ví dụ 3:

• Input: s = "baabb"
• Output: 2
• Giải thích: "baabb" -> "b" -> "". Loại bỏ chuỗi con đối xứng "baab" sau đó "b".

Ràng buộc:

• 1 <= s.length <= 1000
• s[i] là 'a' hoặc 'b'.

Solution

Nếu s đối xứng thì ta xóa luôn s trong 1 bước.

Nếu không thì mỗi bước bạn chọn dãy con gồm tất cả các kí tự giống nhau, tất nhiên là nó đối xứng vì chỉ toàn kí tự giống nhau.

Ví dụ s = "aabbbabab":

1. Xóa dãy con "bbbbb".
2. Xóa dãy con "aaaa".

Cùng lắm là 2 bước.

class Solution: def removePalindromeSub(self, s: str) -> int: return 1 if s == s[::-1] else 2

Leetcode 1460: Make Two Arrays Equal by Reversing Subarrays

Problem

Link: https://leetcode.com/problems/make-two-arrays-equal-by-reversing-subarrays/description/.

Bạn được cung cấp hai mảng số nguyên có cùng độ dài: target và arr. Trong một bước, bạn có thể chọn bất kỳ đoạn con không rỗng nào của arr và đảo ngược nó. Bạn được phép thực hiện bất kỳ số lượng bước nào.

Trả về true nếu bạn có thể làm cho arr bằng với target, hoặc false nếu không thể.

Ví dụ 1:

• Input: target = [1,2,3,4], arr = [2,4,1,3]

• Output: true

• Giải thích: Bạn có thể thực hiện các bước sau để chuyển đổi arr thành target:

  1. Đảo ngược đoạn con [2,4], arr trở thành [4,2,1,3]
  2. Đảo ngược đoạn con [1,3], arr trở thành [4,2,3,1]
  3. Đảo ngược đoạn con [2,3], arr trở thành [4,3,2,1]
  4. Đảo ngược đoạn con [4,3,2,1], arr trở thành [1,2,3,4]

  Có nhiều cách khác nhau để chuyển đổi arr thành target, đây không phải là cách duy nhất để thực hiện điều đó.

Ví dụ 2:

• Input: target = [7], arr = [7]
• Output: true
• Giải thích: arr đã bằng với target mà không cần đảo ngược.

Ví dụ 3:

• Input: target = [3,7,9], arr = [3,7,11]
• Output: false
• Giải thích: arr không có giá trị 9 và nó không bao giờ có thể được chuyển thành target.

Ràng buộc:

• target.length == arr.length
• 1 <= target.length <= 1000
• 1 <= target[i] <= 1000
• 1 <= arr[i] <= 1000

Solution

Để ý rằng, với phép biến đổi đảo ngược mảng con, ta có thể đưa một phần tử đến bất kỳ một vị trí nào ta muốn. Ví dụ muốn đưa arr[5] đến arr[2], ta đảo ngược đoạn con từ 2 đến 5. Các phần tử còn lại trong đoạn cũng bị thay đổi vị trí, nhưng các phần tử ngoài đoạn không bị ảnh hưởng.

Lợi dụng điều này, ta sẽ biến đổi từng phần tử của arr từ trái sang phải cho bằng với phần tử ở vị trí tương ứng trong target.

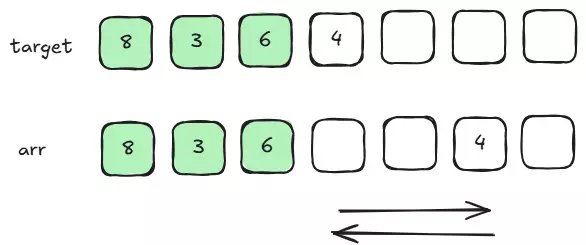
Với mỗi vị trí i, ta tìm phần tử có giá trị bằngtarget[i] trong arr đoạn từ i đến n - 1. Nếu không tìm được phần tử nào, thì tất nhiên không thể biến đổi arr thành target vì không thể thêm phần tử mới. Nếu tìm được, gọi vị trí của phần tử đó là j, ta đảo ngược đoạn con từ i đến j. Bây giờ arr[i] bằng với target[i]. Cứ tiếp tục như vậy đến hết arr.

Ví dụ: target = [1,2,3,4], arr = [2,4,1,3]

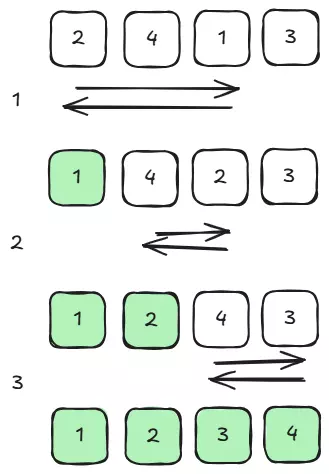
Như vậy, chỉ cần tại mỗi vị trí i đều tìm được j, thì arr sẽ dần được biến đổi thành target, lần lượt từ trái sang. Cho nên thứ tự các phần tử không quan trọng, chỉ cần arr và target chứa những phần tử giống nhau, với số lượng giống nhau, thì arr luôn biến đổi được thành target.

Thật ra bạn có thể nghĩ ra thuật toán khác để sắp xếp lại các phần tử. Điều quan trọng ở đây là bạn luôn có thể biến đổi để sắp xếp arr theo theo một thứ tự tùy ý.

Nên để biết được có thể biến đổi arr thành target hay không, chỉ cần so sánh arr và target có các phần tử giống nhau không. Giống nhau ở đây có nghĩa là số lượng của mỗi giá trị cũng phải giống nhau, ví dụ target có 4 phần tử có giá trị 3 còn arr có 5 phần tử giá trị 3 thì hiển nhiên không biến đổi được rồi vì không thể thêm xóa phần tử.

class Solution: def canBeEqual(self, target: List[int], arr: List[int]) -> bool: return Counter(arr) == Counter(target)

Nếu bạn chưa biết Counter/Dict/Map thì có thể sắp xếp target và arr rồi so sánh:

class Solution: def canBeEqual(self, target: List[int], arr: List[int]) -> bool: return sorted(arr) == sorted(target)

Leetcode 1700: Number of Students Unable to Eat Lunch

Problem

Link: https://leetcode.com/problems/number-of-students-unable-to-eat-lunch/description/.

Nhà ăn của trường cung cấp bánh sandwich hình tròn và hình vuông vào giờ nghỉ trưa, lần lượt được đánh số 0 và 1. Tất cả học sinh xếp hàng. Mỗi học sinh thích bánh sandwich hình vuông hoặc hình tròn.

Số lượng bánh sandwich trong nhà ăn bằng số học sinh. Bánh sandwich được xếp chồng lên một stack. Ở mỗi bước:

• Nếu học sinh ở đầu hàng thích bánh sandwich ở trên cùng của chồng, họ sẽ lấy nó và rời khỏi hàng.
• Ngược lại, họ sẽ bỏ qua bánh sandwich và trở về cuối hàng và đợi đến lượt.

Quá trình này tiếp tục cho đến khi không còn học sinh nào muốn lấy bánh sandwich trên cùng và do đó không thể ăn được.

Bạn được cho hai mảng số nguyên students và sandwiches, trong đó sandwiches[i] là loại bánh sandwich thứ i (i = 0 là trên cùng của chồng) và students[j] là sở thích của học sinh thứ j (j = 0 là đầu hàng). Trả về số học sinh không thể ăn được.

Ví dụ 1:

• Input: students = [1,1,0,0], sandwiches = [0,1,0,1]

• Output: 0

• Giải thích:

  • Học sinh đầu hàng bỏ qua bánh sandwich trên cùng và trở về cuối hàng làm students = [1,0,0,1].
  • Học sinh đầu hàng bỏ qua bánh sandwich trên cùng và trở về cuối hàng làm students = [0,0,1,1].
  • Học sinh đầu hàng lấy bánh sandwich trên cùng và rời khỏi hàng làm students = [0,1,1] và sandwiches = [1,0,1].
  • Học sinh đầu hàng bỏ qua bánh sandwich trên cùng và trở về cuối hàng làm students = [1,1,0].
  • Học sinh đầu hàng lấy bánh sandwich trên cùng và rời khỏi hàng làm students = [1,0] và sandwiches = [0,1].
  • Học sinh đầu hàng bỏ qua bánh sandwich trên cùng và trở về cuối hàng làm students = [0,1].
  • Học sinh đầu hàng lấy bánh sandwich trên cùng và rời khỏi hàng làm students = [1] và sandwiches = [1].
  • Học sinh đầu hàng lấy bánh sandwich trên cùng và rời khỏi hàng làm students = [] và sandwiches = [].

  Do đó tất cả học sinh đều có thể ăn được.

Ví dụ 2:

• Input: students = [1,1,1,0,0,1], sandwiches = [1,0,0,0,1,1]
• Output: 3

Ràng buộc:

• 1 <= students.length, sandwiches.length <= 100
• students.length == sandwiches.length
• sandwiches[i] là 0 hoặc 1.
• students[i] là 0 hoặc 1.

Solution

Thuật toán ngây thơ mô phỏng lại quá trình từng bước:

class Solution: def countStudents(self, students: List[int], sandwiches: List[int]) -> int: while len(students) > 0 and sandwiches[0] in students: front = students.pop(0) if front == sandwiches[0]: sandwiches.pop(0) else: students.append(front) return len(students)

Tuy nhiên, việc liên tục xóa phần tử ở đầu array rất kém hiệu quả. Mỗi lần xóa phần tử ở đầu lại phải cập nhật lại vị trí tất cả các phần tử còn lại. Vậy là bạn phải duyệt qua danh sách students rất rất nhiều lần. Nếu bạn đã biết một chút về cấu trúc dữ liệu chắc bạn cũng đã nhận ra có thể thay thế array bằng queue để thao tác xóa phần tử đỡ tốn kém hơn.

Nhưng bạn còn có thể làm tốt hơn thế.

Để ý, với mỗi miếng sandwich trên cùng, bạn sẽ cứ đẩy học sinh đầu hàng xuống cuối hàng cho đến khi có một học sinh nào đó muốn ăn miếng sandwich này đứng đầu hàng.

Bạn chỉ quan tâm trong hàng còn học sinh nào muốn miếng sandwich này hay không. Nếu không có, quy trình kết thúc. Nếu có, có 1 học sinh muốn miếng sandwich này sẽ được ăn. Cụ thể là học sinh nào thì... cũng không quan trọng.

Như vậy, chúng ta thậm chí không cần phải theo dõi danh sách các học sinh ở trong hàng. Chỉ cần biết có bao nhiêu học sinh nào muốn ăn sandwich 0, bao nhiêu muốn ăn sandwich 1.

class Solution: def countStudents(self, students: List[int], sandwiches: List[int]) -> int: # count_students[i] là số học sinh muốn ăn sandwich loại i count_students = [0, 0] for i in students: count_students[i] += 1 not_eat = len(students) for i in sandwiches: if count_students[i] > 0: count_students[i] -= 1 not_eat -= 1 else: break return not_eat 

Vậy là bạn chỉ cần duyệt qua danh sách students 1 lần, duyệt qua danh sách sandwiches 1 lần. Hiệu quả hơn giải pháp trước đó gấp n lần.

Leetcode 2073: Time Needed to Buy Tickets

Problem

Link: https://leetcode.com/problems/time-needed-to-buy-tickets/description/.

Có n người xếp hàng để mua vé, trong đó người thứ 0 đứng ở đầu hàng và người thứ n - 1 đứng ở cuối hàng.

Bạn được cung cấp một mảng số nguyên là tickets với độ dài n, trong đó số vé mà người thứ i muốn mua là tickets[i].

Mỗi người mất đúng 1 giây để mua một vé. Một người chỉ có thể mua 1 vé mỗi lần và phải quay lại cuối hàng (điều này xảy ra ngay lập tức) để mua thêm vé. Nếu một người không còn vé nào để mua, người đó sẽ rời khỏi hàng.

Trả về thời gian cần thiết để người ở vị trí k (chỉ số bắt đầu là 0) hoàn thành việc mua vé.

Ví dụ 1:

• Input: tickets = [2, 3, 2], k = 2
• Output: 6
• Giải thích:
  • Trong lần đầu tiên, mọi người trong hàng mua một vé và hàng trở thành [1, 2, 1].
  • Trong lần thứ hai, mọi người trong hàng mua một vé và hàng trở thành [0, 1, 0].
  • Người ở vị trí 2 đã mua thành công 2 vé và mất 3 + 3 = 6 giây.

Ví dụ 2:

• Input: tickets = [5, 1, 1, 1], k = 0
• Output: 8
• Giải thích:
  • Trong lần đầu tiên, mọi người trong hàng mua một vé và hàng trở thành [4, 0, 0, 0].
  • Trong 4 lần tiếp theo, chỉ có người ở vị trí 0 mua vé.
  • Người ở vị trí 0 đã mua thành công 5 vé và mất 4 + 1 + 1 + 1 + 1 = 8 giây.

Ràng buộc:

• n == tickets.length
• 1 <= n <= 100
• 1 <= tickets[i] <= 100
• 0 <= k < n

Solution

Thuật toán ngây thơ: mô phỏng lại toàn bộ quá trình mua vé từng bước một đến khi người k mua xong. Bạn có thể dùng cấu trúc dữ liệu queue/deque cho hàng người mua vé để việc thêm xóa phần tử hiệu quả hơn.

class Solution: def timeRequiredToBuy(self, tickets: List[int], k: int) -> int: t = 0 q = deque() for i in range(len(tickets)): q.append(i) while tickets[k] > 0: front = q.popleft() tickets[front] -= 1 t += 1 if tickets[front] > 0: q.append(front) return t

Nhưng với thuật toán này, bạn phải mô phỏng lại toàn bộ quá trình mua vé từng bước một đến khi mua xong. Hãy thử tìm cách làm hiệu quả hơn.

Mỗi lượt mua vé là 1 giây nên thời gian trôi qua cũng tương đương với tổng số vé mọi người đã mua. Hãy thử tính xem mọi người đã mua bao nhiêu vé.

Giả sử ta có hàng đợi 5 người là ["Alice", "Bob, "Carol", "Dave", "Eve"]. Họ cần mua lượng vé tương ứng là [3, 10, 9, 13, 5].

Bạn suy nghĩ kỹ xem, khi Carol mua vé thứ 9 thì mỗi người khác mua được bao nhiêu vé? Nghĩ xong thì đọc tiếp.

Câu trả lời là:

• Alice mua được 3 và đã ra đi.
• Bob mua được 9.
• Dave mua được 8.
• Eve mua được 5 và đã ra đi.

Theo thứ tự ban đầu, người đứng trước có thể mua nhanh hơn người sau 1 vé, nhưng không bao giờ nhiều hơn 1 vé, vì sau khi mua họ sẽ phải về cuối hàng chờ những người khác mua thêm 1 vé.

Khi một người mua người vé thứ x, thì tất cả những người trước anh ta trong thứ tự ban đầu cũng đều đã mua được x vé, hoặc đã mua xong đối với những người cần ít hơn x vé.

Còn những người đứng sau anh ta trong thứ tự ban đầu thì cũng đã mua được x - 1 vé, hoặc đã mua xong hết nếu họ cần ít hơn.

Khi người thứ k vừa mua xong hết vé ta cũng có thể suy ra được mỗi người khác đã mua bao nhiêu vé, từ đó biết tổng số vé đã mua, và biết được thời gian đã trôi qua.

Code:

class Solution: def timeRequiredToBuy(self, tickets: List[int], k: int) -> int: t = 0 for i in range(len(tickets)): if i <= k: t += min(tickets[i], tickets[k]) else: t += min(tickets[i], tickets[k] - 1) return t

Với cách làm này thì bạn chỉ duyệt qua số vé mỗi người mua đúng 1 lần. Cho dù có hàng triệu người, mỗi người phải mua hàng triệu vé, thì thời gian chương trình chạy cũng không đến 1 giây.

Leetcode 1894: Find the Student that Will Replace the Chalk

Problem

Link: https://leetcode.com/problems/find-the-student-that-will-replace-the-chalk/description/

Có n học sinh trong lớp được đánh số từ 0 đến n - 1. Giáo viên sẽ giao cho mỗi học sinh một bài toán bắt đầu từ học sinh số 0, sau đó là học sinh số 1, và cứ tiếp tục như vậy cho đến khi giáo viên đến học sinh số n - 1. Sau đó, giáo viên sẽ bắt đầu lại quá trình, bắt đầu từ học sinh số 0 một lần nữa.

Bạn được cung cấp một mảng số nguyên là chalk và một số nguyên k. Ban đầu có k viên phấn. Khi học sinh số i được giao một bài toán để giải, họ sẽ sử dụng chalk[i] viên phấn để giải bài toán đó. Tuy nhiên, nếu số viên phấn hiện tại ít hơn chalk[i], thì học sinh số i sẽ phải thay phấn.

Trả về chỉ số của học sinh sẽ thay phấn.

Ví dụ 1:

• Input: chalk = [5, 1, 5], k = 22
• Output: 0
• Giải thích:
  • Học sinh số 0 sử dụng 5 viên phấn, nên k = 17.
  • Học sinh số 1 sử dụng 1 viên phấn, nên k = 16.
  • Học sinh số 2 sử dụng 5 viên phấn, nên k = 11.
  • Học sinh số 0 sử dụng 5 viên phấn, nên k = 6.
  • Học sinh số 1 sử dụng 1 viên phấn, nên k = 5.
  • Học sinh số 2 sử dụng 5 viên phấn, nên k = 0.
  • Học sinh số 0 không còn đủ phấn, nên họ sẽ phải thay phấn.

Ví dụ 2:

• Input: chalk = [3, 4, 1, 2], k = 25
• Output: 1
• Giải thích:
  • Học sinh số 0 sử dụng 3 viên phấn, nên k = 22.
  • Học sinh số 1 sử dụng 4 viên phấn, nên k = 18.
  • Học sinh số 2 sử dụng 1 viên phấn, nên k = 17.
  • Học sinh số 3 sử dụng 2 viên phấn, nên k = 15.
  • Học sinh số 0 sử dụng 3 viên phấn, nên k = 12.
  • Học sinh số 1 sử dụng 4 viên phấn, nên k = 8.
  • Học sinh số 2 sử dụng 1 viên phấn, nên k = 7.
  • Học sinh số 3 sử dụng 2 viên phấn, nên k = 5.
  • Học sinh số 0 sử dụng 3 viên phấn, nên k = 2.
  • Học sinh số 1 không còn đủ phấn, nên họ sẽ phải thay phấn.

Ràng buộc:

• chalk.length == n
• 1 <= n <= 10^5
• 1 <= chalk[i] <= 10^5
• 1 <= k <= 10^9

Solution

Thuật toán ngây thơ: Mô phỏng lại quá trình từng học sinh lên làm bài.

class Solution: def chalkReplacer(self, chalk: List[int], k: int) -> int: i = 0 while True: if k < chalk[i]: return i k -= chalk[i] if i + 1 < len(chalk): i = i + 1 else: i = 0

Không đạt, phải không? Time Limit Exceeded.

Vấn đề của thuật toán ngây thơ là khi số k lớn, thì quá trình có thể sẽ kéo dài rất lâu qua nhiều vòng (1 vòng là khi lại quay về lượt của học sinh đầu tiên). Chương trình phải duyệt qua mảng chalk rất nhiều lần. Ví dụ khi k = 1000_000_000, chalk = [1, 1, 1, 1, 1, 1...] (100_000 số 1), thuật toán sẽ duyệt qua chalk 10_000 lần, mà chalk có tận 100_000 phần tử.

Nhưng hãy chú ý vào k sau mỗi một vòng.

1. Sau 1 vòng thì còn 1000_000_000 - 100_000 viên.
2. Sau 2 vòng thì còn 1000_000_000 - 100_000 - 100_000 viên.
3. Sau 3 vòng thì còn 1000_000_000 - 100_000 - 100_000 - 100_000 viên.
4. v.v...

Sau mỗi vòng số lượng phấn bị giảm đi là cố định, và nó chính bằng tổng lượng phấn các học sinh dùng trong một lần.

Bạn có nhất thiết phải lặp qua mỗi vòng và trừ đi từ từ lượng phấn không? Bạn có thể tính được luôn số vòng đúng không?

cycles = int(k / sum(chalk))

Và cũng có thể tính được luôn số phấn còn lại sau cycles vòng:

k = k - cycles * sum(chalk)

Hoặc dùng luôn phép chia lấy phần dư:

k = k % sum(chalk)

Giờ thì phần dư còn lại không đủ cho một vòng nên chỉ cần đi qua danh sách một lần nữa là sẽ hết phấn.

Code:

class Solution: def chalkReplacer(self, chalk: List[int], k: int) -> int: k = k % (sum(chalk)) for i in range(len(chalk)): if k < chalk[i]: return i k -= chalk[i]

Thuật toán này chỉ cần duyệt qua mảng chalk 2 lần, 1 lần để tính tổng số phấn của mỗi vòng và 1 lần nữa để trừ đi lượng phấn tới khi hết phấn.

Leetcode 1509: Minimum Difference Between Largest and Smallest Value in Three Moves

Problem

Link: https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/description/

Bạn được cung cấp một mảng số nguyên nums.

Trong một thao tác, bạn có thể chọn một phần tử của nums và thay đổi nó thành bất kỳ giá trị nào.

Trả về độ chênh lệch nhỏ nhất giữa giá trị lớn nhất và nhỏ nhất của nums sau khi thực hiện tối đa ba thao tác.

(Nói cách khác, bạn có thể thực hiện tối đa 3 thao tác biến đổi để làm thay đổi độ chênh lệch giữa giá trị lớn nhất và nhỏ nhất trong nums, trả về độ chênh lệch nhỏ nhất có thể đạt được).

Ví dụ 1:

• Input: nums = [5, 3, 2, 4]
• Output: 0
• Giải thích:
  • Chúng ta có thể thực hiện tối đa 3 thao tác. Trong thao tác đầu tiên, thay đổi 2 thành 3. nums trở thành [5, 3, 3, 4].
  • Trong thao tác thứ hai, thay đổi 4 thành 3. nums trở thành [5, 3, 3, 3].
  • Trong thao tác thứ ba, thay đổi 5 thành 3. nums trở thành [3, 3, 3, 3].
  • Sau khi thực hiện 3 thao tác, sự khác biệt giữa giá trị nhỏ nhất và lớn nhất là 3 - 3 = 0.

Ví dụ 2:

• Input: nums = [1, 5, 0, 10, 14]
• Output: 1
• Giải thích:
  • Chúng ta có thể thực hiện tối đa 3 thao tác. Trong thao tác đầu tiên, thay đổi 5 thành 0. nums trở thành [1, 0, 0, 10, 14].
  • Trong thao tác thứ hai, thay đổi 10 thành 0. nums trở thành [1, 0, 0, 0, 14].
  • Trong thao tác thứ ba, thay đổi 14 thành 1. nums trở thành [1, 0, 0, 0, 1].
  • Sau khi thực hiện 3 thao tác, sự khác biệt giữa giá trị nhỏ nhất và lớn nhất là 1 - 0 = 1.

Ví dụ 3:

• Input: nums = [3, 100, 20]
• Output: 0
• Giải thích:
  • Chúng ta có thể thực hiện tối đa 3 thao tác. Trong thao tác đầu tiên, thay đổi 100 thành 7. nums trở thành [3, 7, 20].
  • Trong thao tác thứ hai, thay đổi 20 thành 7. nums trở thành [3, 7, 7].
  • Trong thao tác thứ ba, thay đổi 3 thành 7. nums trở thành [7, 7, 7].
  • Sau khi thực hiện 3 thao tác, sự khác biệt giữa giá trị nhỏ nhất và lớn nhất là 7 - 7 = 0.

Ràng buộc:

• 1 <= nums.length <= 10^5
• -10^9 <= nums[i] <= 10^9

Solution

Tất nhiên bạn không nên biến đổi một phần tử mà làm giảm min hay tăng max của mảng vì nó sẽ làm tăng độ chênh lệch.

Biến đổi một phần tử mà không phải min hay max cũng chẳng có tác dụng gì. Ví dụ nums = [1, 5, 0, 10, 14], biến 10 thành 11 độ chênh lệch vẫn là 13.

Bạn nên biến đổi những phần tử là max hoặc min, và biến đổi thành giá trị nào đó nằm trong khoảng min mới và max mới, cụ thể là bao nhiêu cũng không quan trọng vì chúng ta chỉ quan tâm độ chênh lệch giữa min và max.

Nhìn chung bạn chỉ cần biến đổi các phần tử nhỏ nhất, nhỏ nhì, nhỏ ba, lớn nhất, lớn nhì, lớn ba. Như vậy số lượng trường hợp để kiểm tra cũng không còn bao nhiêu.

• Biến đổi 3 phần tử nhỏ nhất.
• Biến đổi 2 phần tử nhỏ nhất và 1 phần tử lớn nhất.
• Biến đổi 1 phần tử nhỏ nhất và 2 phần tử lớn nhất.
• Biến đổi 3 phần tử lớn nhất.

Ngoài ra, với mảng chỉ có 4 phần tử hoặc ít hơn bạn có thể biến đổi cho các phần tử bằng nhau để độ chênh lệch là 0.

class Solution: def minDifference(self, nums: List[int]) -> int: if len(nums) <= 4: return 0 nums = sorted(nums) return min( nums[-1] - nums[3], # Biến đổi 3 phần tử nhỏ nhất nên nums[3] trở thành nhỏ nhất nums[-2] - nums[2], # Biến đổi 1 phần tử lớn nhất nên nums[-2] trở thành lớn nhất nums[-3] - nums[1], nums[-4] - nums[0] )

Mảng được sắp xếp lại để có thể dễ dàng truy xuất các phần tử nhỏ nhất, nhỏ nhì, lớn nhất, lớn nhì, v.v...

Thật ra chỉ cần quan tâm đến vài phần tử nhỏ nhất và lớn nhất nên cũng không nhất thiết phải sắp xếp lại toàn bộ mảng. Thuật toán vẫn có thể tối ưu hơn nữa. Bạn có thể dùng heap/priority queue để tìm nhanh các phần tử lớn nhất, nhỏ nhất (nếu bạn là người mới bắt đầu thì có thể bỏ qua phần này, cách trên đã đủ để đạt ở bài này).

class Solution: def minDifference(self, nums: List[int]) -> int: if len(nums) <= 4: return 0 smallest = heapq.nsmallest(4, nums) largest = heapq.nlargest(4, nums) return min( largest[0] - smallest[3], largest[1] - smallest[2], largest[2] - smallest[1], largest[3] - smallest[0] )

Kết

Những câu hỏi trên có làm thay đổi quan niệm của bạn về thuật toán không?

Như bạn đã thấy, những vấn đề ở trên hoàn toàn không hề đòi hỏi phải biết đến thuật toán hay cấu trúc dữ liệu cao siêu nào cả. Thậm chí, người biết nhiều thuật toán cũng có thể không giải quyết được vấn đề. Có vô vàn vấn đề, ai mà thuộc hết thuật toán cho mọi tình huống. Quan trọng là phải rèn luyện kỹ năng quan sát, tư duy, suy luận, v.v. để có thể nghĩ ra được thuật toán giải quyết vấn đề mới gặp.

Nhưng tôi cũng không bảo bạn không cần học thêm thuật toán. Các thuật toán phổ thông có thể giúp bạn giải quyết một phần của vấn đề. Thường thấy nhất là thuật toán sắp xếp. May là nó thường được viết sẵn rồi, nhưng không phải các thuật toán khác cũng thế. Đôi khi bạn cần kết hợp các thuật toán để giải quyết vấn đề. Hoặc bạn có thể tinh chỉnh lại một thuật toán cho phù hợp với tình huống cụ thể. Bạn cũng nên cố gắng hiểu nguyên lý, ý tưởng của thuật toán thay vì chỉ học thuộc lòng. Thú thật, tôi chả thuộc thuật toán nào, nhưng đa số tôi hiểu nên có thể viết lại được. Như vậy bạn có thể tinh chỉnh, học được tư duy, kỹ thuật, trick để có thể áp dụng trong các trường hợp khác. Mà biết đâu hiểu thuật toán rồi bạn lại có thể cải tiến hay phát minh ra thuật toán tốt hơn.

Mong rằng bài viết này sẽ giúp bạn hiểu hơn về thuật toán, cải thiện kỹ năng lập trình của mình và truyền cảm hứng cho bạn trong việc rèn luyện thuật toán.