I. Ma trận kề (Adjacency Matrix)

Giả sử $G=(V, E)$ là một đa đồ thị có số đỉnh là $N$. Coi rằng các đỉnh được đánh số từ $1$ tới $N$. Khi đó, ta có thể biểu diễn đồ thị bằng một ma trận vuông $adj$ kích thước $N\times N$, trong đó:

• $adj_{u, v}=0,$ nếu $(u, v) \notin E, u\ne v$.
• $adj_{u, v}=x,$ nếu $(u, v) \in E, u \ne v$ và $x$ là số lượng cạnh nối giữa $u$ và $v$.
• Đối với $adj_{u, u}$ với $\forall u:1\le u \le N$, có thể đặt giá trị tùy theo mục đích, thông thường nên đặt bằng $0$.

Cài đặt: Việc cài đặt cạnh sẽ thay đổi tùy vào đồ thị là có hướng hay vô hướng. Dưới đây sẽ trình bày cài đặt cho đồ thị vô hướng:

void enter_adjacency_matrix()
{ cin >> N >> M; // Nhập số đỉnh và số cạnh của đồ thị. for (int i = 1; i <= M; ++i) { int u, v; cin >> u >> v; adj[u][v]++; // Tăng số cạnh giữa u và v. adj[v][u]++; // Nếu là đồ thị có hướng thì không có dòng này. }
}

Ví dụ: Đồ thị $G(V, E)$ dưới đây có $5$ đỉnh, $6$ cạnh:

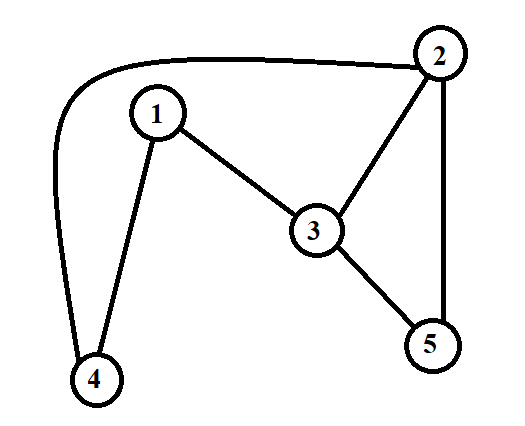
Ma trận kề của nó sẽ có dạng như sau:

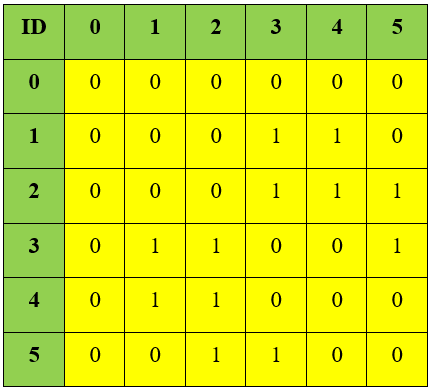
Ưu điểm của ma trận kề:

• Đơn giản, dễ cài đặt.
• Để kiểm tra hai đỉnh $u$ và $v$ có kề nhau hay không, chỉ việc kiểm tra trong $O(1)$ bằng phép so sánh $a_{u, v} \ne 0$.

Nhược điểm của ma trận kề:

• Luôn luôn tiêu tốn $N^2$ ô nhớ để lưu trữ ma trận kề, dù là trong trường hợp đồ thị ít cạnh hay nhiều cạnh.
• Để xét một đỉnh $u$ kề với những đỉnh nào, buộc phải duyệt toàn bộ các đỉnh $v$ và kiểm tra điều kiện $a_{u, v} \ne 0$. Như vậy kể cả đỉnh $u$ không kề với đỉnh nào, chúng ta vẫn phải duyệt mất $O(N)$ để biết được điều đó.

Phù hợp khi nào: Trong các bài toán đồ thị có số lượng đỉnh ít (thường là không vượt quá $300$).

II. Danh sách cạnh (Edge List)

Trong trường hợp biết trước đồ thị có $N$ đỉnh, $M$ cạnh, ta có thể biểu diễn đồ thị dưới dạng một danh sách lưu các cạnh $(u, v)$ của đồ thị đó (nếu là đồ thị có hướng thì mỗi cặp $(u, v)$ ứng với một cung $u \rightarrow v$). Vector hoặc mảng là một kiểu dữ liệu rất phù hợp để lưu trữ danh sách cạnh.

Cài đặt:

vector < pair < int, int > > edge_list; // Danh sách cạnh. void enter_edge_list()
{ cin >> N >> M; for (int i = 1; i <= M; ++i) { int u, v; cin >> u >> v; edge_list.push_back({u, v}); }
}

Ví dụ: Đồ thị $G(V, E)$ dưới đây $5$ đỉnh, $6$ cạnh theo thứ tự là: $(1, 3), (1, 4), (3, 4), (3, 2), (5, 3), (2, 5)$:

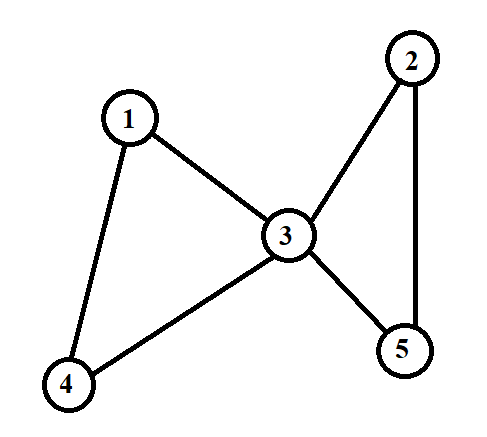
Danh sách cạnh của nó được biểu diễn bằng một vector \text{edge_list} như sau:

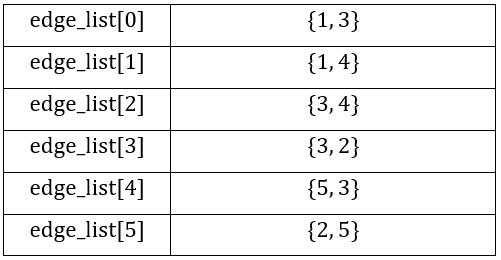
Ưu điểm của danh sách cạnh:

• Trong trường hợp đồ thị ít cạnh, cách biểu diễn này sẽ giúp tiết kiệm không gian lưu trữ.
• Ở một số trường hợp đặc biệt, ta phải xét tất cả các cạnh trên đồ thị thì phương pháp cài đặt này giúp việc duyệt cạnh dễ dàng hơn trong $O(M)$ (ví dụ giải thuật tìm cây khung nhỏ nhất Kruskal).

Nhược điểm của danh sách cạnh: Trong trường hợp cần duyệt các đỉnh kề với một đỉnh $u$, bắt buộc phải duyệt qua mọi cạnh, lọc ra các cạnh có chứa đỉnh $u$ và xét đỉnh còn lại. Điều này sẽ tốn thời gian nếu đồ thị có nhiều cạnh.

Phù hợp khi nào: Trong các bài toán cần duyệt toàn bộ cạnh, tiêu biểu như trong giải thuật Kruskal.

III. Danh sách kề (Adjacency List)

Để khắc phục nhược điểm của ma trận kề và danh sách cạnh, người ta sử dụng danh sách kề (cũng là cách thường xuyên sử dụng nhất trong các bài toán đồ thị). Trong cách biểu diễn này, với mỗi đỉnh u của đồ thị, ta sẽ tạo ra một dánh sách $adj_u$ là các đỉnh kề với nó. Việc cài đặt $adj_u$ có thể thực hiện dễ dàng với vector.

Cài đặt:

vector < int > adj[maxn + 1]; // Danh sách kề, maxn là số đỉnh tối đa của đồ thị. void enter_adjacency_list()
{ cin >> N >> M; // Số đỉnh và số cạnh của đồ thị. for (int i = 1; i <= M; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); // Đưa v vào danh sách kề với u. adj[v].push_back(u); // Nếu là đồ thị có hướng thì không có dòng này. }
}

Ví dụ: Đồ thị $G(V, E)$ dưới đây gồm $5$ đỉnh, $4$ cạnh:

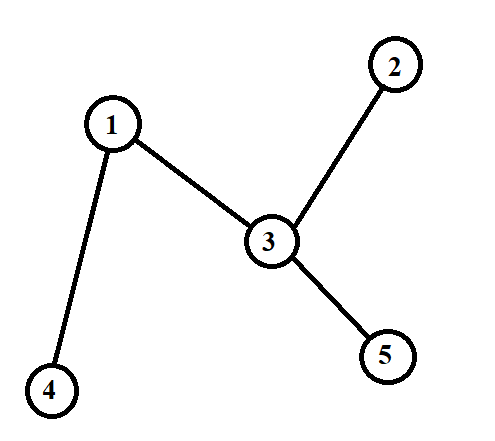
Danh sách kề của nó có thể biểu diễn bằng một mảng $\text{adj}[6]$ gồm các vector (kích thước mảng là $6$ do không có đỉnh số $0$), mỗi vector $\text{adj}[u]$ lưu danh sách kề của đỉnh $u$:

Ưu điểm của danh sách kề:

• Duyệt đỉnh kề và các cạnh của đồ thị rất nhanh.
• Tiết kiệm không gian lưu trữ, do vector là kiểu dữ liệu với bộ nhớ động, sẽ chỉ tạo ra các ô nhớ tương ứng với số lượng đỉnh kề.

Nhược điểm của danh sách kề: Khi cần kiểm tra $(u, v)$ có phải là một cạnh của đồ thị hay không thì bắt buộc phải duyệt toàn bộ danh sách kề của $u$ hoặc của $v$.

Phù hợp khi nào: Hầu hết trong mọi bài toán đồ thị đều nên sử dụng, chỉ trừ các bài toán cần duyệt toàn bộ cạnh của đồ thị.

IV. Tài liệu tham khảo

• Sách Giải thuật và Lập trình - thầy Lê Minh Hoàng.
• Tài liệu giáo khoa chuyên Tin quyển 1 - thầy Hồ Sĩ Đàm.