Như mình đã trình bày trong bài viết trước, tìm kiếm nhị phân trên một mảng thể hiện sự hiệu quả. Tuy nhiên, hiệu suất của việc tìm kiếm trên mảng bị giảm đi rất nhiều khi dữ liệu trong tập dữ liệu thay đổi thường xuyên. Với tập dữ liệu động, ta phải áp dụng cấu trúc dữ liệu khác để duy trì hiệu suất tìm kiếm ở mức chấp nhận được.

Cây tìm kiếm là cấu trúc dữ liệu phổ biến nhất được sử dụng để lưu trữ các tập dữ liệu động. Loại cây tìm kiếm phổ biến nhất là cây tìm kiếm nhị phân, trong đó mỗi nút bên trong cây có nhiều nhất hai nút con. Một loại cây tìm kiếm khác, được gọi là B-Tree, là một cây n-ary được thiết kế để dễ dàng lưu trữ trên đĩa nhớ.

Phân tích thuật toán

Đặt vấn đề

Input và output cho các thuật toán sử dụng cây tìm kiếm giống như đối với Tìm kiếm nhị phân. Mỗi phần tử $e$ từ một tập hợp $C$ để được lưu trữ trong cây tìm kiếm cần có một hoặc nhiều thuộc tính có thể được sử dụng như một khóa $k$. Các phần tử cũng phải có các thuộc tính phân biệt chính nó với các phần tử khác trong tập hợp. Cây tìm kiếm sẽ được sử dụng lưu trữ các phần tử của tập $C$.

Rò rỉ bộ nhớ là một vấn đề nghiêm trọng đối với các lập trình viên. Khi một chương trình chạy trong một thời gian dài, chẳng hạn như nhiều ứng dụng server được sử dụng trong các hệ thống ngày nay, rò rỉ bộ nhớ sẽ khiến chương trình vượt quá lượng bộ nhớ được cấp cho quy trình của nó và sau đó bị sập, thường dẫn đến những hậu quả tai hại.

Người ta có thể viết một chương trình để giám sát việc phân phối bộ nhớ và báo cáo về cấu hình bộ nhớ của chương trình để phát hiện sự xuất hiện của rò rỉ bộ nhớ. Một trình biên dịch bộ nhớ như vậy có thể được viết khá đơn giản bằng cách viết các hàm malloc() và free() ghi lại thông tin thích hợp trước khi cấp phát và giải phóng bộ nhớ. Chúng ta muốn ghi lại mọi cấp phát bộ nhớ và khi bộ nhớ đó được giải phóng, chúng ta phải xóa nó khỏi tập hợp cấp phát đang hoạt động.

Trong tình huống được mô tả, ta không biết trước về số lượng phần tử cần lưu trữ. Tìm kiếm dựa trên hàm băm sử dụng được, nhưng ta có thể chọn kích thước bảng băm quá nhỏ để sử dụng tài nguyên hiệu quả. Một chiến lược tìm kiếm thay thế là sử dụng cây tìm kiếm nhị phân. Cây tìm kiếm nhị phân hoạt động tốt với dữ liệu động, nơi thường xuyên thực hiện thao tác chèn và xóa.

Cây tìm kiếm nhị phân $T$, là một tập hợp hữu hạn các nút được xác định bằng thuộc tính có thứ tự hoặc khóa. Tập hợp các nút có thể rỗng hoặc nó có thể chứa một nút gốc $n_r$. Mỗi nút $n$ tham chiếu đến hai cây tìm kiếm nhị phân, $T_l$ và $T_r$, tuân theo thuộc tính rằng nếu $k$ là khóa của nút $n$, thì tất cả các khóa trong $T_l$ là $≤k$ và tất cả các khóa trong $T_r$ là $≥k$. Hình dưới cho thấy một ví dụ nhỏ về cây nhị phân. Mỗi nút có một khóa là số nguyên xác định nút.

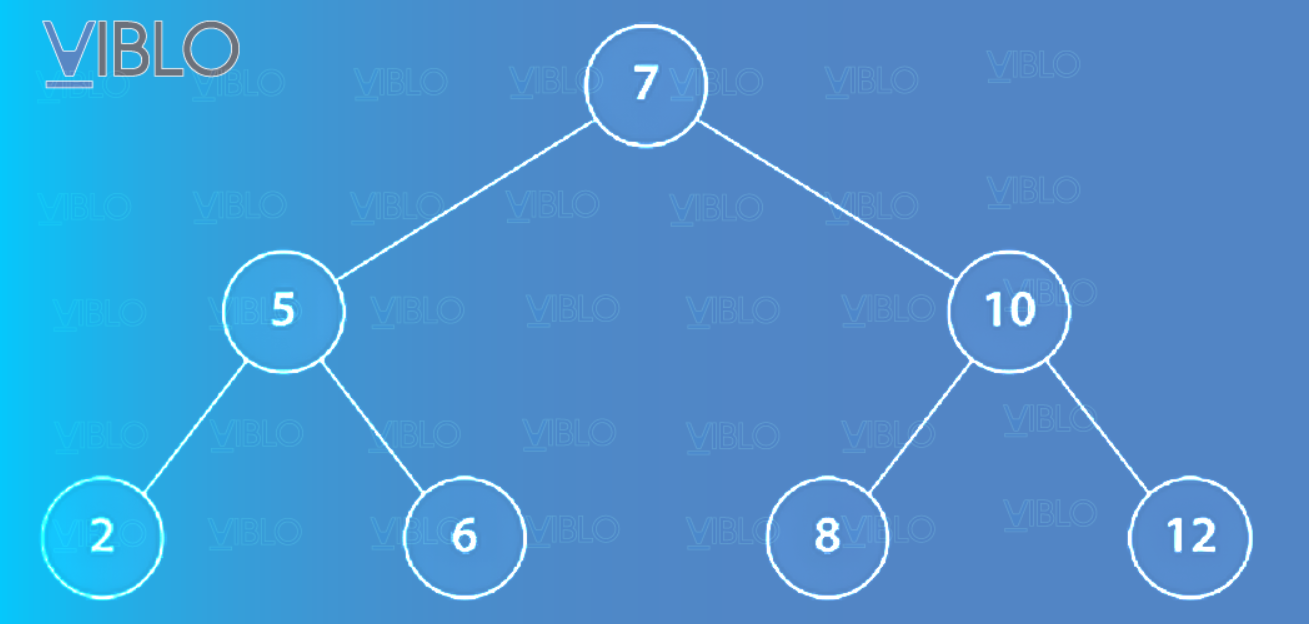
Bạn có thể thấy rằng việc tìm một khóa trong cây ở hình yêu cầu kiểm tra nhiều nhất ba nút, bắt đầu với nút gốc. Ta thấy cây hoàn toàn cân đối. Có nghĩa là, mỗi nút có bất kỳ nút con nào đều có đúng hai nút con. Một cây nhị phân cân bằng hoàn hảo có $2^{n – 1}$ nút với $n≥1$ và chiều cao là $n – 1$.

Cây có thể không phải lúc nào cũng cân đối (như hình dưới). Ở đây cây đóng vai trò như một list (danh sách).

Điều kiện sử dụng

Nếu chúng ta chỉ cần xác định vị trí của một phần tử nào đó, lựa chọn đầu tiên nên là giải pháp dựa trên hàm băm. Để sử dụng cây tìm kiếm nhị phân, ta cần cân nhắc các yếu tố:

• Kích thước tập dữ liệu không xác định và việc cài đặt phải có khả năng xử lý bất kỳ kích thước có thể nào làm cho phù hợp với bộ nhớ.

• Tập dữ liệu có tính động cao và sẽ có nhiều lần chèn và xóa trong suốt thời gian tồn tại của cấu trúc dữ liệu.

• Ứng dụng yêu cầu duyệt dữ liệu theo thứ tự tăng dần hoặc giảm dần.

Khi quyết định sử dụng cây tìm kiếm, ta phải đưa ra các phương án thiết kế cây sao cho phù hợp:

• Nếu ta cần duyệt tập dữ liệu theo thứ tự bắt đầu từ bất kỳ nút cụ thể nào, thì các con trỏ thích hợp đến các nút cha phải được đưa vào cấu trúc nút.

• Nếu dữ liệu là động, chúng ta phải thiết kế sao cho cây cân đối.

Trong hầu hết các ứng dụng, chúng ta cần cân đối cây để tránh cây bị lệch, đó là có một vài nhánh dài hơn hoặc ngắn hơn nhiều so với các nhánh khác. Một loại cây nhị phân cân đôi được sử dụng gọi là cây đỏ đen. Các cây đỏ đen xấp xỉ cân đối. Sử dụng một cây đỏ đen đảm bảo rằng không có nhánh nào có chiều cao hơn hai lần so với bất kỳ nhánh nào khác. Cây đỏ đen thỏa mãn các điều kiện sau:

• Mọi nút đều được dán nhãn đỏ hoặc đen.

• Gốc có màu đen.

• Mọi nút lá đều chứa giá trị rỗng và có màu đen.

• Tất cả các nút màu đỏ có hai nút con màu đen.

• Mọi đường đi đơn giản từ một nút đến một trong các nút lá con của nó đều chứa cùng một số nút đen.

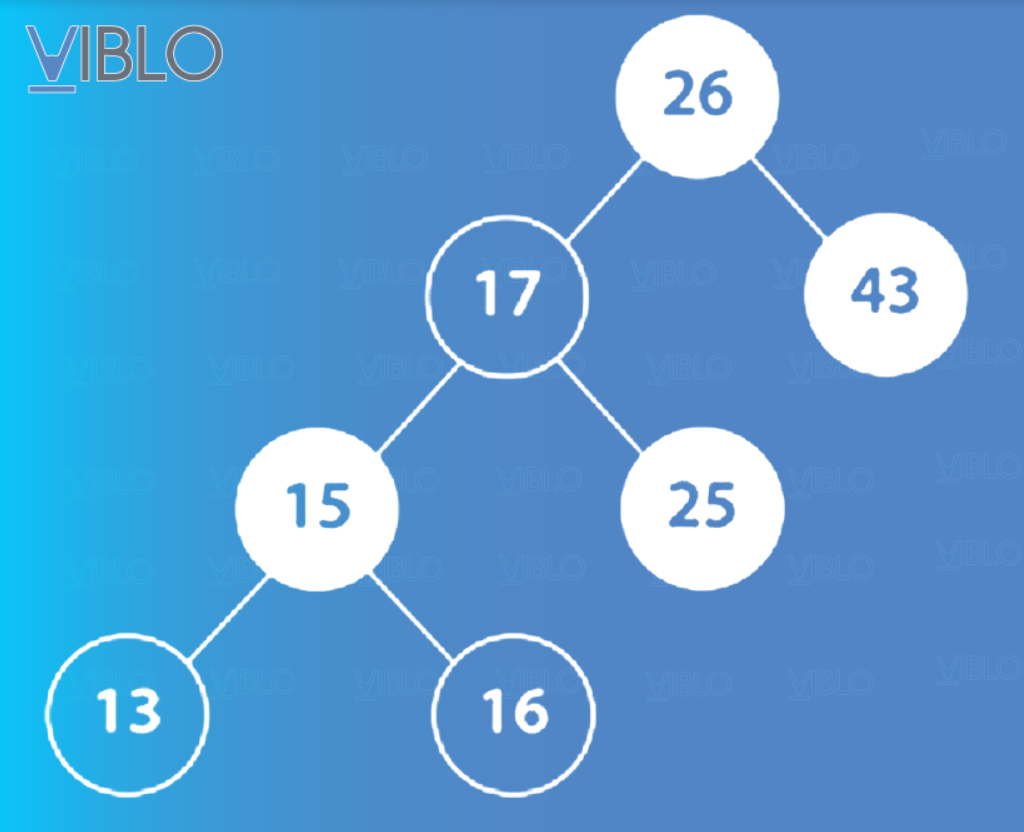
Trong các sơ đồ tiếp theo, mình không hiển thị các nút lá có giá trị null. Khi nhìn vào sơ đồ, bạn hãy tưởng tượng rằng mỗi nút lá trong sơ đồ thực sự có hai nút con màu đen và chúng có giá trị null.

Mô tả thuật toán

Tìm kiếm trên cây đỏ đen không khác gì so với tìm kiếm bất kỳ trên cây nhị phân nào. Bắt đầu từ gốc, ta kiểm tra từng nút để tìm giá trị khóa đã cho, chuyển sang nút con bên trái nếu giá trị khóa nhỏ hơn giá trị khóa cần tìm kiếm và chuyển sang nút con bên phải nếu giá trị khóa lớn hơn.

Code java của thuật toán tìm kiếm nhị phân trên cây:

public V search(K k) { BalancedBinaryNode<K,V> p = root; while (p != null) { int cmp = compare(k, p.key); if (cmp == 0) { return p.value; } else if (cmp < 0) { p = p.left; } else { p = p.right; } } // not found return null;
}

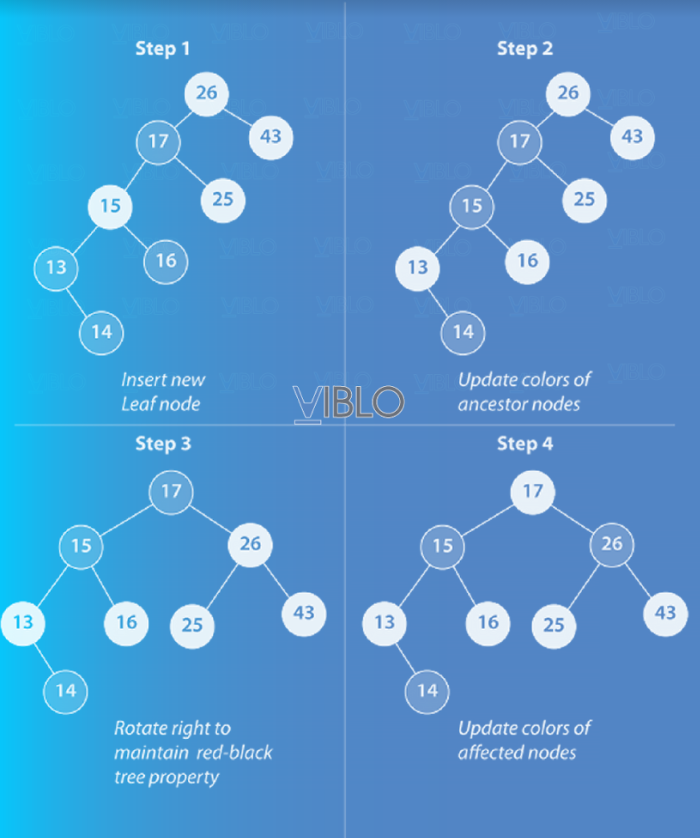
Để chèn một nút vào cây đỏ đen, ta cần tìm vị trí thích hợp trong cây mà nút mới sẽ được đặt. Khi chúng ta thêm giá trị 14 vào cây trong hình 3, một nút mới chứa 14 sẽ trở thành nút con bên phải của nút lá chứa giá trị 13 (có nhãn “Step 1” trong hình 4). Sau khi chèn vào, các thuộc tính của cây đỏ đen bị xâm phạm nên cây phải tự điều chỉnh. Ở bước 2, màu sắc của các nút được cập nhật để đảm bảo điều kiện 4 của cây đỏ đen. Ở bước 3, cây được xoay sang phải để đảm bảo điều kiện 5 của cây đỏ đen. Cuối cùng, ở Bước 4, màu sắc của các nút được cập nhật để đảm bảo điều kiện 4 của cây.

Thao tác cơ bản khi thay đổi cấu trúc cây là xoay về một nút. Ta sửa đổi các nút con trong cây để thực hiện thao tác xoay. Hình dưới cho thấy kết quả của việc xoay trái hoặc phải về một nút. Có thể xoay cây bên trái về nút a để thành cây bên phải. Tương tự, bạn có thể thực hiện một phép xoay bên phải về nút b để từ cây bên phải thành cây bên trái.

Ta thấy rằng để thực hiện các phép xoay, cấu trúc nút trong cây đỏ đen cần có các con trỏ cha. Code java để thực hiện xoay trái được trình bày bên dưới (xoay phải tương tự):

protected void rotateLeft(BalancedBinaryNode<K,V> p) { BalancedBinaryNode<K,V> r = p.right; p.right = r.left; if (r.left != null) r.left.parent = p; r.parent = p.parent; if (p.parent == null) root = r; else if (p.parent.left == p) p.parent.left = r; else p.parent.right = r; r.left = p; p.parent = r;
}

Lưu ý rằng các phép xoay đảm bảo thuộc tính cây tìm kiếm nhị phân vì thứ tự của các nút là không thay đổi. Khi giá trị mới được chèn, cây sẽ tự cập nhật để khôi phục điều kiện 4 và 5 của cây đỏ đen.

Nhận xét

Cây đỏ đen hay các cây nhị phân cân đối khác yêu cầu phải code dài hơn so với cây tìm kiếm nhị phân đơn giản. Sự đánh đổi này đáng giá về hiệu suất thời gian chạy . Cây đỏ đen có hai yêu cầu lưu trữ đối với cấu trúc dữ liệu được sử dụng cho các nút như sau:

• Mỗi nút yêu cầu bộ nhớ để lưu trữ màu của nút. Đây là mức tối thiểu là một bit, nhưng trong thực tế, hầu hết các cài đặt sử dụng ít nhất một byte.

• Mọi nút phải có một liên kết cha, đây không phải là một yêu cầu đối với cây tìm kiếm nhị phân.

Cây đỏ đen cũng yêu cầu một nút có giá trị null ở gốc. Người ta có thể thực hiện điều này bằng cách sử dụng một nút có giá trị null và làm cho tất cả các con trỏ của nút lá trỏ đến nó.

Phân tích độ phức tạp

Độ phức tạp thời gian trung bình của tìm kiếm trên cây giống với tìm kiếm nhị phân, đó là $O (\log n)$. Tuy nhiên, giờ đây việc chèn và xóa cũng có thể được thực hiện trong thời gian $O (\log n)$.

Biến thể

Có cấu trúc cây cân đối khác. Phổ biến nhất là cây AVL. Cây đỏ đen và các cây nhị phân cân đối khác là những lựa chọn tốt để tìm kiếm trong bộ nhớ. Khi tập dữ liệu trở nên quá lớn không thể lưu trong bộ nhớ, một loại cây khác thường được sử dụng: cây n-way, trong đó mỗi nút có $n> 2$ nút con. Một phiên bản chung của những cây như vậy được gọi là B-tree, hoạt động rất tốt trong việc giảm thiểu số lần truy cập đĩa để tìm một mục cụ thể trong tập dữ liệu lớn. B-tree thường được sử dụng khi triển khai cơ sở dữ liệu quan hệ.

Tổng kết

Vậy là trong bài viết mình đã trình bày những kiến thức về cây tìm kiếm nhị phân cùng với các ưu nhược điểm. Nhờ tính chất của cây tìm kiếm nhị phân mà hiệu suất tìm kiếm được cải thiện khi làm việc với dữ liệu liên tục thay đổi. Do đó, hãy cân nhắc sử dụng cây tìm kiếm nhị phân nếu bạn muốn tăng tốc chương trình của mình.

Tài liệu tham khảo

1. Giải thuật và lập trình - Thầy Lê Minh Hoàng
2. cp-algorithms.com
3. Handbook Competitive Programming - Antti Laaksonen
4. Competitve programming 3 - Steven Halim, Felix Halim