I. Mở đầu

Công thức bao hàm - loại trừ là một công thức sử dụng để tính lực lượng (số lượng phần tử) của hợp của nhiều tập hợp. Công thức được phát biểu như sau: "Để tính lực lượng của hợp của nhiều tập hợp, ta tính tổng lực lượng các tập hợp đó, rồi trừ đi lực lượng của giao của các cặp hai tập hợp khác nhau, rồi cộng lực lượng của giao các bộ ba tập hợp khác nhau, rồi trừ đi lực lượng của các bộ bốn tập hợp, và cứ thế cho đến khi ta xét đến giao của tất cả các tập hợp."

Đối với các tập hợp, công thức có thể được viết ở dạng như sau: Giả sử có $N$ tập hợp $A_1, A_2, A_3,..., A_N$. Lực lượng của hợp của $N$ tập hợp là:

Ta có thể minh họa công thức bằng một sơ đồ Venn trong trường hợp $N = 3$ như sau:

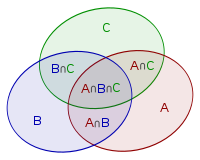
Như sơ đồ, ta thấy lực lượng của $A \cap B \cap C$ bằng tổng lực lượng của $A, B, C$ trừ đi lực lượng của các giao $A \cap B, B \cap C, C \cap A$ rồi cộng thêm lực lượng của $A \cap B \cap C$:

Bằng phương pháp tương tự ta có thể minh họa được công thức với $N$ tập hợp.

Ví dụ: Đếm số lượng số từ $1$ tới $N$ và không chia hết cho số nào trong tập $\{2, 3, 5\}$:

Ta có thể biến đổi bài toán thành đếm phần bù: Đếm số lượng phần tử chia hết cho ít nhất một số trong tập $\{2, 3, 5\}$ rồi lấy $N$ trừ đi số lượng đó. Đặt $A$ là tập hợp các phần tử chia hết cho $2,\ B$ là tập hợp các phần tử chia hết cho $3, \ C$ là tập hợp các phần tử chia hết cho $5$ từ 1 tới $N$. Cần tính $|A \cup B \cup C|$. Dựa vào công thức bao hàm, loại trừ, ta có:

Đoạn mã tính toán công thức trên có thể viết đơn giản như sau:

int count_numbers(int N)
{ return N - N / 2 - N / 3 - N / 5 + N / (2 * 3) + N / (3 * 5) + N / (2 * 5) - N / (2 * 3 * 5); }

Công thức bao hàm - loại trừ có sức mạnh cực kì to lớn trong các bài toán đếm của toán học tổ hợp. Sau đây chúng ta sẽ cùng nghiên cứu một số bài toán ứng dụng của công thức này!

II. Bài toán ví dụ

1. Chính phương và Lập phương

Đề bài

Dãy số chính phương và lập phương là dãy gồm các số chính phương và lập phương. Sau đây là một vài số đầu tiên trong dãy: $1, 4, 8, 9, 16, \dots$

Yêu cầu: Cho số nguyên dương $n$. Hãy xác định trong đoạn $[1; n]$ có bao nhiêu số nằm trong dãy số chính phương và lập phương.

Input:

• Dòng đầu tiên chứa số nguyên $t$ — số lượng test case.
• $t$ dòng tiếp theo tương ứng với $t$ test case, mỗi dòng chứa số nguyên $n$.

Ràng buộc:

• $1 \le t \le 20$.
• $1 \le n \le 10^9$.

Output:

• Gồm $t$ dòng là kết quả tương ứng với $t$ test case.

Sample Input:

6
10
1
25
1000000000
999999999
500000000

Sample Output:

4
1
6
32591
32590
23125

Ý tưởng

Dãy số gồm các số chính phương sẽ là dãy gồm các số có dạng $x^2,$ với $x \ge 1$ và $x^2 \le n$.

Tương tự, dãy số gồm các số lập phương sẽ là dãy gồm các số có dạng $x^3,$ với $x \ge 1$ và $x^3 \le n$.

Tuy nhiên, trong hai dãy số đó sẽ có những số bị trùng nhau, tức là vừa là số chính phương, vừa là số lập phương. Các số đó có dạng $x^{2 \times 3} = x^6,$ với $x \ge 1$ và $x^6 \le n$. Ta sẽ tạo ra dãy $A$ gồm các số chính phương, dãy $B$ gồm các số lập phương và dãy $C$ gồm các số dạng lũy thừa bậc $6$.

Gọi $cnt_1$ là số lượng số chính phương không vượt quá $n, cnt_2$ là số lượng số lập phương không vượt quá $n$ và $cnt_3$ là số lượng số vừa là chính phương vừa là lập phương không vượt quá $n$. Ba giá trị này có thể dễ dàng tính ra được bằng cách tìm kiếm nhị phân trên ba mảng $A, B, C$. Sau đó, theo công thức bao hàm loại trừ, số lượng số nằm trong dãy chính phương - lập phương từ $1$ tới $n$ sẽ là:

$$cnt_1 + cnt_2 - cnt_3$$

Để đẩy nhanh tốc độ giải thuật, ta sẽ khởi tạo trước ba mảng $A, B, C$ tới các số không vượt quá $10^9,$ rồi ứng với mỗi giá trị $n$ ở từng test case thì thực hiện tìm kiếm nhị phân và tính toán như công thức nói trên.

Độ phức tạp: $\approx O\big(t \times sqrt(n)\big)$.

Cài đặt

#include <bits/stdc++.h> using namespace std; vector < int > a, b, c; void init()
{ for (int i = 1; i * i <= 1e9; ++i) a.push_back(i * i); for (int i = 1; i * i * i <= 1e9; ++i) b.push_back(i * i * i); for (int i = 1; i * i * i * i * i * i <= 1e9; ++i) c.push_back(i * i * i * i * i * i);
} void solve_testcase(int n)
{ int cnt1 = (upper_bound(a.begin(), a.end(), n) - a.begin()); int cnt2 = (upper_bound(b.begin(), b.end(), n) - b.begin()); int cnt3 = (upper_bound(c.begin(), c.end(), n) - c.begin()); cout << cnt1 + cnt2 - cnt3 << '\n';
} int main()
{ ios_base::sync_with_stdio(0); cin.tie(0); init(); int t; cin >> t; while(t--) { int n; cin >> n; solve_testcase(n); } return 0;
} 

2. Ba - Năm - Bảy

Đề bài

Thầy giáo cho UcoderA định nghĩa về dãy số ba - năm - bảy như sau: Là một dãy số tăng dần, các phần tử của dãy chia hết cho ít nhất một trong ba số $3$, $5$ và $7$. Ví dụ một vài phần tử đầu tiên của dãy: $\{3; 5; 6; 7; 9; 10; 12; 14; 15; 18; 20; 21; 24; 25; \dots\}$

Yêu cầu: Cho số nguyên $k,$ hãy xác định giá trị phần tử thứ $k$ của dãy số ba - năm - bảy?

Input:

• Một dòng duy nhất chứa số nguyên $k$.

Ràng buộc:

• $1 \le k \le 10^{18}$.

Output:

• Phần tử thứ $k$ của dãy số ba-năm-bảy.

Sample Input 1

13

Sample Output 1

24

Sample Input 2

100

Sample Output 2

185

Ý tưởng

Với các subtask nhỏ, ta có thể sử dụng vòng lặp sau đó tăng dần số $x$ đang xét cho đến khi đó là phần tử thứ $k$ ở trong dãy ba-năm-bảy.

Độ phức tạp thuật toán lúc này là $O(n)$. Ta cần một thuật toán tốt hơn.

Để cải tiến cách làm, các bạn cần sử dụng chặt nhị phân và kiến thức về bao hàm bù trừ.

Với mỗi số $x,$ ta có thể xác định được trước nó có bao nhiêu số chia hết cho $3, 5$ hoặc $7$ bằng cách sau:

Gọi số lượng số bé hơn hoặc bằng $x$ chia hết cho $3$ là $cnt[3] = \left\lfloor\frac{x}{3}\right\rfloor$, định nghĩa tương tự cho $cnt[5]$ và $cnt[7]$. Số lượng số chia hết cho cả $3$ và $5$ là $cnt[3\cdot5] = cnt[15] = \left\lfloor\frac{x}{15}\right\rfloor$, định nghĩa tương tự cho $cnt[3\cdot7] = cnt[21]$ và $cnt[7\cdot5] = cnt[35]$. Số lượng số chia hết cho cả $3$, $5$ và $7$ là $cnt[3\cdot5\cdot7] = cnt[105]$.

Ta thấy rằng tổng $cnt[3] + cnt[5] + cnt[7]$ sẽ bị trùng với nhau một lượng phần $cnt[15]$, $cnt[21]$ và $cnt[35]$ nên ta phải trừ đi lượng đấy, nhưng nếu trừ đi thì ta sẽ mất một lượng $cnt[105]$ nên phải cộng bù vào. Vậy số lượng số chia hết cho $3$, $5$ hoặc $7$ bé hơn hoặc bằng $x$ là:

$$cnt[3] + cnt[5] + cnt[7] - cnt[15] - cnt[21] - cnt[35] + cnt[108]$$

Có được công thức trên, bạn đọc có thể sử dụng kĩ thuật chặt nhị phân tìm kết quả để tìm số $x$ bé nhất sao cho từ $3$ đến $x$ có đúng $k$ số chia hết cho $3$, $5$ hoặc $7$.

Độ phức tạp thuật toán: $O(n\log n)$.

Cài đặt

#include <bits/stdc++.h> using namespace std; typedef long long ll; int main()
{ ll k; cin >> k; ll l = 3, r = 2e18, ans; while(l <= r) { ll x = (l + r) / 2LL; ll cnt3 = x / 3LL; ll cnt5 = x / 5LL; ll cnt7 = x / 7LL; ll cnt15 = x / 15LL; ll cnt21 = x / 21LL; ll cnt35 = x / 35LL; ll cnt105 = x / 105LL; if (cnt3 + cnt7 + cnt5 - cnt15 - cnt21 - cnt35 + cnt105 >= k) r = x - 1, ans = x; else l = x + 1; } cout << ans; return 0;
}

3. Dãy chữ số đầy đủ

Đề bài

Cho trước số nguyên dương $n$. Một dãy $a_1,a_2,\dots,a_N$ được gọi là dãy đầy đủ nếu thỏa mãn những điều sau đây:

• $0 \le a_i \le 9$.
• Tồn tại một vị trí $i$ nào đó sao cho $a_i=0$.
• Tồn tại một vị trí $i$ nào đó sao cho $a_i=9$.

Yêu cầu: Hãy đếm số số dãy đẩy đủ có độ dài $n$. Kết quả có thể rất lớn, hãy in ra số dư khi chia cho $10^9+7$.

Input:

• Dòng duy nhất chứa một số $n$.

Constraints:

• $1 \le n \le 10^6$.

Output:

• Một số duy nhất là số dư của kết quả sau khi chia cho $10^9 + 7$.

Sample Input 1:

2

Sample Output 1:

2

Giải thích:

Có $2$ dãy là $(0,9)$ và $(9,0)$.

Ý tưởng

Có tổng cộng $10^n$ dãy $A$ độ dài $n$ và $0\le a_i \le 9$.

Thay vì đếm trực tiếp, ta sẽ sử dụng kĩ thuật đếm phần bù trong bài toán này. Cụ thể, ta sẽ trừ đi những dãy không phải là dãy đầy đủ, hay những dãy không tồn tại $a_i=0$ hoặc không tồn tại $a_i=9$. Số lượng đó như sau:

• Có tổng cộng $9^n$ dãy $A$ không tồn tại $a_i=0$.
• Có tổng cộng $9^n$ dãy $A$ không tồn tại $a_i=9$.
• Có tổng cộng $8^n$ dãy $A$ không tồn tại $a_i=0$ và $a_i=9$.

Theo nguyên lí bao hàm - loại trừ, ta suy ra có $9^n + 9^n - 8^n$ dãy $A$ không tồn tại $a_i=0$ hoặc không tồn tại $a_i=9$.

Như vậy đáp án là $10^n - (9^n + 9^n - 8^n)$.

Độ phức tạp: $O(n)$ hoặc $O\big(\log_2(n)\big)$ tùy vào cài đặt để tính các lũy thừa. Lưu ý kết quả có phép trừ, do đó nếu sử dụng ngôn ngữ C++ thì cần chú ý tránh để xảy ra trường hợp kết quả bị âm sau khi chia dư cho $10^9 + 7$.

Cài đặt

#include <bits/stdc++.h>
#define int long long using namespace std; const int mod = 1e9 + 7; int binary_exponentiation(int a, int b, int mod)
{ if (b == 0) return 1LL; int half = binary_exponentiation(a, b / 2LL, mod) % mod; if (b & 1) return (((half * half) % mod) * (a % mod)) % mod; else return (half * half) % mod;
} main()
{ int n; cin >> n; int x = binary_exponentiation(10, n, mod); int y = (2 * binary_exponentiation(9, n, mod) % mod - binary_exponentiation(8, n, mod) + mod) % mod; cout << (x - y + mod) % mod; return 0;
}

III. Tài liệu tham khảo

• https://www.geeksforgeeks.org/eulerian-number/
• https://vnoi.info/wiki/translate/he/Number-Theory-5
• https://www.hackerearth.com/practice/notes/number-theory-ii/
• https://vnoi.info/wiki/translate/he/Number-Theory-7.md
• Tài liệu giáo khoa chuyên Tin quyển 1 - thầy Hồ Sĩ Đàm