I. Tổng quan

Những lý thuyết cơ bản của lý thuyết đồ thị chỉ mới được đề xuất từ thế kỷ XVIII, bắt đầu từ một bài báo của Leonhard Euler về bài toán $7$ cây cầu ở Königsberg - một bài toán cực kỳ nổi tiếng:

Thành phố Königsberg thuộc Đức (nay là Kaliningrad thuộc CHLB Nga) được chia làm $4$ vùng bằng các nhánh của con sông Pregel giống như hình vẽ bên dưới. Vào năm $1736,$ người ta đã xây $7$ cây cầu nối các vùng này với nhau. Người dân ở đây tự hỏi, liệu có cách nào xuất phát tại một địa điểm trong thành phố ( $1$ trong $4$ vùng), đi qua $7$ chiếc cầu, mỗi chiếc đúng một lần rồi lại quay trở về điểm xuất phát hay không?

Euler đã giải quyết thành công bài toán này bằng cách mô tả bản đồ khu vực bởi một đa đồ thị, với các khu vực là các đỉnh và những chiếc cầu là các cạnh nối. Bài toán nói trên có thể được tổng quát hóa thành bài toán: Có tồn tại chu trình trong đa đồ thị, đi qua tất cả các cạnh và mỗi cạnh đúng một lần hay không?

Bởi vì Leonhard Euler là người đã giải bài toán này, nên dạng chu trình đi qua tất cả các cạnh, mỗi cạnh đúng một lần được gọi là chu trình Euler, như một cách để tri ân nhà bác học vĩ đại của lịch sử loài người.

II. Các khái niệm và định lý

Có $4$ khái niệm mà chúng ta cần nắm vững trước khi đi vào tìm hiểu về giải thuật tìm chu trình Euler:

Chu trình đơn chứa tất cả các cạnh của đồ thị được gọi là chu trình Euler.
Đường đi đơn chứa tất cả các cạnh của đồ thị được gọi là đường đi Euler.
Một đồ thị có chu trình Euler được gọi là đồ thị Euler.
Một đồ thị có đường đi Euler được gọi là đồ thị nửa Euler.

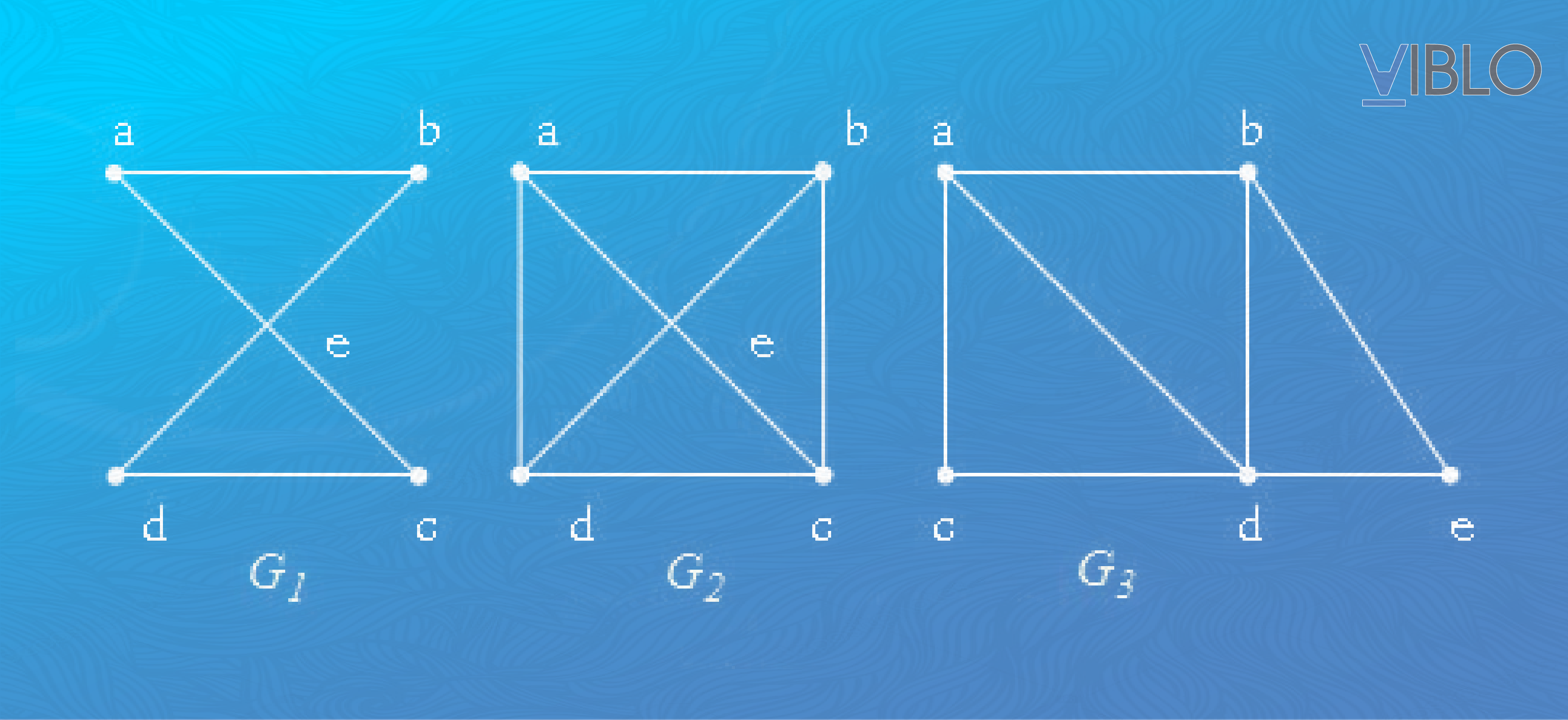
Trong các đồ thị trên, đồ thị $G_1$ có chu trình Euler là $(a, e, c, d, e, b, a);$ đồ thị $G_2$ không có chu trình Euler nhưng có đường đi Euler là $(a, c, d, e, b, a, d, b),$ nên nó là đồ thị nửa Euler; còn đồ thị $G_3$ không có chu trình Euler lẫn đường đi Euler.

Ngoài ra, có một số định lý quan trọng sẽ hỗ trợ cho quá trình phát triển thuật toán tìm chu trình Euler:

Định lý 1

Một đồ thị vô hướng liên thông $G=(V,E)$ có chu trình Euler khi và chỉ khi mọi đỉnh của nó đều có bậc chẵn: $deg⁡(v)≡0 \ (\text{mod } 2); ∀v∈V$ .

Chứng minh: Nếu $G$ có chu trình Euler, thì khi đi dọc theo chu trình đó, mỗi khi đi qua một đỉnh thì bậc của đỉnh đó tăng thêm $2$ (có hai cạnh liên thuộc ở hai đầu). Mà chu trình Euler lại đi qua tất cả các cạnh, nên suy ra mọi đỉnh của đồ thị đều có bậc chẵn. Từ đó cũng suy ra điều ngược lại: Nếu $G$ liên thông và các đỉnh đều có bậc chẵn, thì ta sẽ xây dựng được thuật toán tìm chu trình Euler trên đồ thị.

Hệ quả 1

Một đồ thị vô hướng liên thông $G = (V, E)$ có đường đi Euler khi và chỉ khi nó có đúng $2$ đỉnh bậc lẻ.

Chứng minh: Nếu $G$ có đường đi Euler thì chỉ có đỉnh bắt đầu và đỉnh kết thúc đường đi có bậc lẻ, còn mọi đỉnh khác trên đường đi đều có bậc chẵn. Ngược lại, nếu đồ thị liên thông có đúng $2$ đỉnh bậc lẻ thì ta sẽ thêm vào một cạnh giả nối hai đỉnh bậc lẻ đó, rồi tìm chu trình Euler. Sau khi tìm xong, loại bỏ cạnh giả đi là thu được đường đi Euler.

Định lý 2

Một đồ thị có hướng liên thông yếu $G = (V, E)$ có chu trình Euler thì mọi đỉnh của nó có bán bậc ra bằng bán bậc vào: $deg^{+}(v) = deg^{-}(v), \forall v \in V$ . Ngược lại, nếu $G$ liên thông yếu và mọi đỉnh của nó có bán bậc ra bằng bán bậc vào, thì $G$ có chu trình Euler (đồng nghĩa với việc $G$ là đồ thị liên thông mạnh).

Chứng minh: Tương tự cách chứng minh định lý $1$ .

Hệ quả 2

Một đồ thị có hướng liên thông yếu $G = (V, E)$ có đường đi Euler nhưng không có chu trình Euler nếu và chỉ nếu tồn tại đúng hai đỉnh $s, t \in V$ sao cho:

$deg^{+}(s) - deg^{-}(s) = eg^{+}(t) - deg^{-}(t) = 1$

còn tất cả các đỉnh còn lại của đồ thị đều có bán bậc ra bằng bán bậc vào.

Việc chứng minh định lý số $1$ sẽ giúp chúng ta xây dựng được một thuật toán hữu ích để tìm chu trình Euler trên đồ thị Euler, đó là giải thuật Fleury.

III. Giải thuật Fleury tìm chu trình Euler

1. Phát biểu bài toán

Cho đa đồ thị vô hướng liên thông $G$ gồm $n$ đỉnh, $m$ cạnh. Hãy tìm ra một chu trình Euler của đồ thị?

Input:

Dòng đầu tiên chứa số nguyên dương $n$ - số đỉnh của đồ thị $(1 \le n \le 100)$ .
Các dòng tiếp theo, mỗi dòng chứa ba số nguyên $u, v, k$ - cho biết giữa hai đỉnh $u$ và $v$ có $k$ cạnh nối.

Output:

Ghi ra một chu trình Euler tìm được. Nếu đồ thị ban đầu không phải đồ thị Euler, in ra $0$ .

Sample Input:

Sample Output:

1 2 3 1 3 4 1

2. Giải thuật cơ sở

Ý tưởng

Trước hết, ta sẽ một số khái niệm như sau để thống nhất thuật toán trên cả đồ thị vô hướng và có hướng:

Nếu nói cạnh $(u,v)$ thì hiểu là cạnh nối hai đỉnh $u$ và $v$ trên đồ thị vô hướng, hiểu là cung nối từ đỉnh $u$ tới đỉnh $v$ trên đồ thị có hướng.
Gọi cạnh $(u,v)$ là cạnh “một đi không trở lại” nếu như từ $u$ ta đi tới $v$ theo cạnh đó, sau đó xóa cạnh này đi thì không còn cách nào từ $v$ quay trở lại $u$ cả.

Như vậy, giải thuật Fleury đơn giản nhất có thể phát biểu như sau:

Xuất phát từ một đỉnh, ta đi tùy ý theo các cạnh, tuân theo hai nguyên tắc:

Một là xóa bỏ cạnh vừa đi qua.
Hai là chỉ chọn đi vào cạnh "một đi không trở lại" nếu như không còn cạnh nào khác để chọn. Việc kiểm tra một cạnh $(u, v)$ có phải là cạnh "một đi không trở lại" hay không có thể thực hiện bằng cách: Thử xóa cạnh đó đi rồi dùng $BFS$ để tìm đường đi từ $v$ tới $u,$ nếu không tìm được thì cạnh đó chắc chắn là cạnh "một đi không trở lại".

Ta sẽ cài đặt giải thuật bằng cách sử dụng một ma trận kề $\text{adj}[u][v]$ để biểu diễn đồ thị cho thuận tiện khi thực hiện thao tác xóa cạnh, ngoài ra có thêm một hàm kiểm tra xem đồ thị có phải là đồ thị Euler hay không.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define task "Euler." using namespace std; typedef int arr[1001];
typedef int arr2[1001][1001]; // Nhập dữ liệu cho đồ thị. Thao tác này có thể dễ dàng điều chỉnh // khi đề bài thay đổi cách nhập liệu.
void enter(int &n, arr2 adj, arr deg)
{ cin >> n; int u, v, k; while (cin >> u >> v >> k) { adj[u][v] = adj[v][u] = k; deg[u] += k; deg[v] += k; }
} void dfs(int n, int u, int cnt_comps, arr2 adj, arr number) // Đếm số TPLT của đồ thị.
{ number[u] = cnt_comps; for (int v = 1; v <= n; ++v) if (!number[v] && adj[u][v]) dfs(n, v, cnt_comps, adj, number);
} // Kiểm tra đồ thị có phải đồ thị Euler không.
bool check_euler_graph(int n, arr2 adj, arr deg)
{ // Đếm số thành phần liên thông của đồ thị. int cnt_comps = 0; arr number; for (int u = 1; u <= n; ++u) if (!number[u]) { ++cnt_comps; dfs(n, u, cnt_comps, adj, number); } // Nếu đồ thị không liên thông thì nó không phải đồ thị Euler. if (cnt_comps > 1) return false; // Nếu tồn tại đỉnh có bậc lẻ thì cũng không phải đồ thị Euler. for (int u = 1; u <= n; ++u) if (deg[u] % 2 == 1) return false; return true;
} // Kiểm tra xem nếu xóa cạnh (u, v) thì có thể đi ngược từ v về u không.
bool can_go_back(int n, arr2 adj, int u, int v)
{ // Thử xóa cạnh (u, v), tức là số cạnh nối giảm đi 1. --adj[u][v]; --adj[v][u]; // Sau khi xóa cạnh (u, v), thử bfs từ v tới u xem có đi được nữa không. bool is_free[n + 1]; fill(is_free + 1, is_free + n + 1, true); queue < int > path; path.push(v); while (!path.empty()) { int cur = path.front(); path.pop(); if (cur == u) break; for (int next_v = 1; next_v <= n; ++next_v) if (is_free[next_v] && adj[cur][next_v]) { is_free[next_v] = false; path.push(next_v); } } // Nối lại cạnh (u, v) do lúc nãy đã thử xóa cạnh này đi. ++adj[u][v]; ++adj[v][u]; return !is_free[u];
} // Giải thuật Fleury tìm chu trình Euler trên đồ thị.
void fleury(int n, arr2 adj, arr deg)
{ // Đồ thị không phải đồ thị Euler -> In ra 0. if (!check_euler_graph(n, adj, deg)) { cout << 0; return; } int cur_vertex = 1, next_v = 0; vector < int > circuit; step.push_back(cur_vertex); do { next_v = 0; // Lần lượt chọn các cạnh liên thuộc với đỉnh hiện tại // trong chu trình đang xét. for (int v = 1; v <= n; ++v) if (adj[cur_vertex][v]) { next_v = v; // Ưu tiên chọn cạnh không phải là cạnh "một đi không trở lại". if (can_go_back(n, adj, cur_vertex, next_v)) break; } // Tìm được 1 cạnh nối chưa bị xóa có thể đi được. if (next_v != 0) { // Xóa cạnh nối đó đi. --adj[cur_vertex][next_v]; --adj[next_v][cur_vertex]; step.push_back(next_v); // Đưa đỉnh này vào danh sách các đỉnh trên chu trình. cur_vertex = next_v; } } while (next_v != 0); // In ra chu trình tìm được. for (int u: circuit) cout << u << ' ';
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int n; arr2 adj; arr deg; enter(n, adj, deg); fleury(n, adj, deg); return 0;
}

3. Cải tiến với ngăn xếp

Trong trường hợp đồ thị có số cạnh vừa phải, có thể cải tiến bằng giải thuật như sau: Bắt đầu từ một chu trình đơn $C$ bất kỳ, chu trình này tìm được bằng cách xuất phát từ một đỉnh bất kỳ, đi tùy ý theo các cạnh cho tới khi quay trở về đỉnh xuất phát (lưu ý đi qua cạnh nào xóa luôn cạnh đó). Khi đó, có thể xảy ra hai trường hợp:

Nếu chu trình $C$ này chứa tất cả các cạnh của đồ thị thì đó là một chu trình Euler.
Nếu không, ta xét các đỉnh $u$ thuộc chu trình $C,$ nếu còn một cạnh liên thuộc nào đó của $u$ chưa bị xóa thì ta lại tiếp tục đi từ $u,$ theo các cạnh tùy ý tới khi quay trở về $u$ để thu được một chu trình đơn khác qua $u$ .
Cuối cùng loại bỏ $u$ khỏi chu trình $C$ và chèn chu trình mới tìm được vào đúng vị trí của $u$ vừa xóa, ta sẽ thu được một chu trình $C’$ mới lớn hơn chu trình $C$ ban đầu. Cứ làm như vậy cho tới khi tìm được chu trình Euler.

Để cài đặt việc xóa và thêm đỉnh một cách hiệu quả, ta sẽ sử dụng một ngăn xếp $\text{vertexes}$ để kiểm soát các đỉnh $u$ trên chu trình. Mọi cài đặt khác vẫn giống như giải thuật cơ bản, chỉ riêng hàm xác để xác định một cạnh $(u, v)$ có phải cạnh "một đi không trở lại" hay không sẽ không cần thiết nữa.

Một lưu ý nho nhỏ là đối với ngôn ngữ lập trình C++, nếu như số cạnh trên đồ thị quá dày, thì quá trình $\text{DFS}$ sẽ phải gọi đệ quy rất sâu, dẫn đến tràn ngăn xếp của bộ nhớ (ngăn xếp lưu các lời gọi đệ quy). Để giải quyết vấn đề này, các bạn cần mở tăng dung lượng mặc định của ngăn xếp trong C++, xem hướng dẫn đối với các IDE dưới đây:

IDE Code::Blocks: <a href="https://codeforces.com/blog/entry/15874" title="" target="_blank">Hướng dẫn<a>.
IDE Visual Studio Code: <a href="https://docs.microsoft.com/en-us/cpp/build/reference/f-set-stack-size?view=msvc-170&viewFallbackFrom=vs-2019" title="" target="_blank">Hướng dẫn<a>.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define task "Euler." using namespace std; typedef int arr[1001];
typedef int arr2[1001][1001]; // Nhập dữ liệu cho đồ thị. Thao tác này có thể dễ dàng điều chỉnh // khi đề bài thay đổi cách nhập liệu.
void enter(int &n, arr2 adj, arr deg)
{ cin >> n; int u, v, k; while (cin >> u >> v >> k) { adj[u][v] = adj[v][u] = k; deg[u] += k; deg[v] += k; }
} void dfs(int n, int u, int cnt_comps, arr2 adj, arr number) // Đếm số TPLT của đồ thị.
{ number[u] = cnt_comps; for (int v = 1; v <= n; ++v) if (!number[v] && adj[u][v]) dfs(n, v, cnt_comps, adj, number);
} // Kiểm tra đồ thị có phải đồ thị Euler không.
bool check_euler_graph(int n, arr2 adj, arr deg)
{ // Đếm số thành phần liên thông của đồ thị. int cnt_comps = 0; arr number; for (int u = 1; u <= n; ++u) if (!number[u]) { ++cnt_comps; dfs(n, u, cnt_comps, adj, number); } // Nếu đồ thị không liên thông thì nó không phải đồ thị Euler. if (cnt_comps > 1) return false; // Nếu tồn tại đỉnh có bậc lẻ thì cũng không phải đồ thị Euler. for (int u = 1; u <= n; ++u) if (deg[u] % 2 == 1) return false; return true;
} // Giải thuật Fleury tìm chu trình Euler trên đồ thị, cải tiến với stack.
void fleury_stack(int n, arr2 adj, arr deg)
{ // Đồ thị không phải đồ thị Euler -> In ra 0. if (!check_euler_graph(n, adj, deg)) { cout << 0; return; } stack < int > vertexes; vector < int > circuit; vertexes.push(1); while (!vertexes.empty()) { int u = vertexes.top(); for (int v = 1; v <= n; ++v) if (adj[u][v]) // Nếu có cạnh (u, v) { // Xóa cạnh khỏi đồ thị. --adj[u][v]; --adj[v][u]; // Đẩy tiếp v vào ngăn xếp. vertexes.push(v); break; } // Nếu đỉnh ở đầu ngăn xếp vẫn là u, suy ra vòng lặp trên không tìm được // đỉnh nào kề với u, vậy nó là một đỉnh thuộc chu trình. if (u == vertexes.top()) { circuit.push_back(u); vertexes.pop(); } } // In ra chu trình tìm được, nhưng theo thứ tự ngược lại vì các đỉnh. // đẩy vào stack bị ngược so với các cung định hướng. Đối với đồ thị // vô hướng thì điều này không quan trọng, nhưng nếu là đồ thị có hướng // thì bắt buộc phải làm như vậy, nếu không chu trình sẽ sai so với các // cung của đồ thị ban đầu. for (int i = circuit.size() - 1; i >= 0; --i) cout << circuit[i] << ' ';
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int n; arr2 adj; arr deg; enter(n, adj, deg); fleury_stack(n, adj, deg); return 0;
}

IV. Tài liệu tham khảo

<a href="https://cuongquach.com/ebook-giai-thuat-va-lap-trinh-lmh-pdf.html" title="" target="_blank">Sách Giải thuật và Lập trình - thầy Lê Minh Hoàng</a>.
<a href="https://downloadsachmienphi.com/tai-lieu-giao-khoa-chuyen-tin-quyen-1/" title="" target="_blank">Tài liệu giáo khoa chuyên Tin quyển 1 - thầy Hồ Sĩ Đàm</a>.
https://vi.wikipedia.org/wiki/Đồ_thị_Euler
https://www.geeksforgeeks.org/fleurys-algorithm-for-printing-eulerian-path/
https://www.geeksforgeeks.org/eulerian-path-and-circuit/

Đồ thị Euler và Chu trình Euler

I. Tổng quan

II. Các khái niệm và định lý

Định lý 1

Hệ quả 1

Định lý 2

Hệ quả 2

III. Giải thuật Fleury tìm chu trình Euler

1. Phát biểu bài toán

2. Giải thuật cơ sở

Ý tưởng

Cài đặt

3. Cải tiến với ngăn xếp

Cài đặt

IV. Tài liệu tham khảo

Bình luận

Bài viết tương tự

Thuật toán quay lui (Backtracking)

Các thuật toán cơ bản trong AI - Phân biệt Best First Search và Uniform Cost Search (UCS)

Sử dụng vector trong lập trình C++ - giải bài toán lập trình muôn thủa

MÔ PHỎNG THUẬT TOÁN VƯƠNG HẠO TRONG PROLOG

A* Search Algorithm

Python: Jump Search