I. Tổng quan

Khái niệm về đường đi và chu trình Hamilton được đưa ra bởi William Rowan Hamilton vào năm $1856,$ sau khi ông thiết một trò chơi trên khối đa diện $20$ đỉnh, $30$ cạnh, $12$ mặt, mỗi cạnh là một ngũ giác đều và người chơi cần chọn các cạnh để thành lập một đường đi qua $5$ đỉnh cho trước (còn gọi là trò chơi Icosian).

Bài toán tổng quát được Hamilton đưa ra là: Tìm một chu trình đơn đi qua tất cả các đỉnh trên đồ thị, mỗi đỉnh đúng một lần sau đó quay trở về điểm xuất phát. Cho đến nay, bài toán này vẫn chưa có lời giải đối với trường hợp đồ thị tổng quát. Những bài toán liên quan tới chu trình Hamilton đều là những bài toán NP - hard. Mọi thuật toán tìm kiếm chu trình Hamilton hiện nay đều chỉ thiết kế dựa trên mô hình duyệt mà thôi.

II. Các khái niệm và định lý

Cho đồ thị $G = (V, E)$ có $n$ đỉnh. Vẫn tương tự như đồ thị Euler, chúng ta sẽ có một số khái niệm đối với đồ thị Hamilton:

Một chu trình $x_1,x_2,…,x_n,x_1$ được gọi là chu trình Hamilton nếu $x_i≠x_j; ∀i,j:1≤i<j≤n$ .
Đường đi $x_1,x_2,…,x_n$ được gọi là đường đi Hamilton nếu $x_i≠x_j; ∀i,j:1≤i<j≤n$ .
Đồ thị có chu trình Hamilton được gọi là đồ thị Hamilton.
Đồ thị có đường đi Hamilton được gọi là đồ thị nửa Hamilton. Lưu ý, chu trình Hamilton không phải là đường đi Hamilton (do đỉnh xuất phát được thăm tới $2$ lần), khác với chu trình Euler cũng chính là đường đi Euler. Ngoài ra, quy ước rằng đồ thị chỉ gồm $1$ đỉnh là đồ thị Hamilton, nhưng đồ thị gồm $2$ đỉnh liên thông sẽ không phải đồ thị Hamilton.

Các bạn có thể xem một số hình vẽ đồ thị dưới đây để hiểu hơn về các khái niệm:

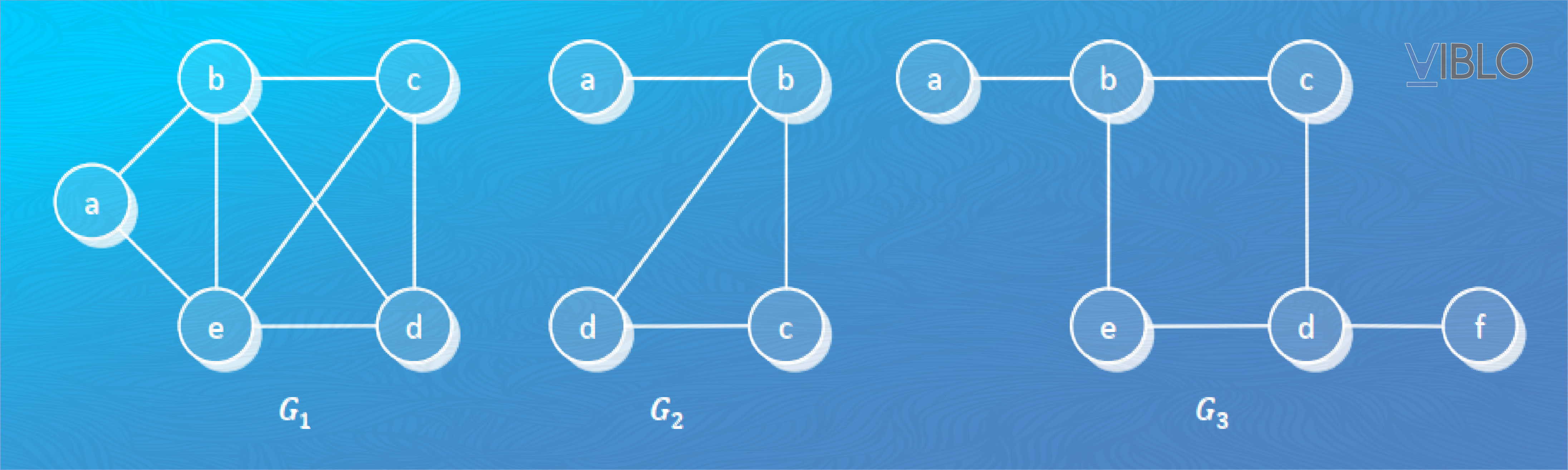
Trong các đồ thị trên, đồ thị $G_1$ có chu trình Hamilton là $(a, b, c, d, e, a);$ đồ thị $G_2$ không có chu trình Hamilton nhưng có đường đi Hamilton $(a, b, c, d);$ còn đồ thị $G_3$ không có cả đường đi Hamilton lẫn chu trình Hamilton.

Những định lý dưới đây cho chúng ta một vài dấu hiệu nhận biết một đồ thị có phải đồ thị Hamilton hay không:

Định lý 1

Xét với đồ thị vô hướng $G,$ trong đó tồn tại $k$ đỉnh sao cho nếu xóa đi $k$ đỉnh này cùng với những cạnh liên thuộc của chúng thì đồ thị nhận được sẽ có nhiều hơn $k$ thành phần liên thông. Khi đó, khẳng định $G$ không phải là đồ thị Hamilton.

Định lý 2 (Định lý Dirak, 1952)

Xét đơn đồ thị vô hướng $G = (V, E)$ có $n$ đỉnh $(n \ge 3)$ . Nếu mọi đỉnh đều có bậc không nhỏ hơn $\left\lfloor{\frac{n}{2}}\right\rfloor$ thì $G$ là đồ thị Hamilton.

Định lý 3 (Định lý Ghouila - Houiri, 1960)

Xét đơn đồ thị có hướng liên thông mạnh $G = (V, E)$ có $n$ đỉnh. Nếu trên phiên bản vô hướng của $G,$ mọi đỉnh đều có bậc không nhỏ hơn $n$ thì $G$ là đồ thị Hamilton.

Định lý 4 (Định lý Ore, 1960)

Xét đơn đồ thị vô hướng $G = (V, E)$ có $n$ đỉnh $(n \ge 3)$ . Xét mọi cặp đỉnh không kề nhau, nếu không có cặp đỉnh nào có tổng bậc nhỏ hơn $n$ thì $G$ là đồ thị Hamilton.

Định lý 5 (Định lý Meynie, 1973)

Xét đơn đồ thị có hướng liên thông mạnh $G = (V, E)$ có $n$ đỉnh. Nếu trên phiên bản vô hướng của $G,$ mọi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn $2n - 1$ thì $G$ là đồ thị Hamilton.

Định lý 6 (Định lý Bondy - Chvátal, 1972)

Xét đồ thị vô hướng $G = (V, E)$ có $n$ đỉnh, với mỗi cặp đỉnh không kề nhau $(u, v)$ mà $deg(u) + deg(v) \ge n,$ ta thêm một cạnh nối $u$ và $v$ . Cứ làm như vậy tới khi không thêm được cạnh nào nữa, thì ta thu được một bao đóng của đồ thị $G,$ kí hiệu $cl(G)$ . Khi đó, $G$ là đồ thị Hamilton nếu và chỉ nếu $cl(G)$ là đồ thị Hamilton.

III. Thuật toán tìm chu trình Hamilton

1. Phát biểu bài toán

Cho đồ thị vô hướng liên thông $G$ có $n$ đỉnh và $m$ cạnh. Hãy tìm ra các chu trình Hamilton xuất phát từ đỉnh $1$ của đồ thị?

Input:

Dòng đầu tiên chứa hai số nguyên dương $n$ và $m$ - số đỉnh và số cạnh của đồ thị $(1 \le n \le 100, 1 \le m \le 100)$ .
$m$ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương $u, v$ - thể hiện một cạnh nối giữa hai đỉnh $u$ và $v$ của đồ thị.

Output:

Ghi ra các chu trình Hamilton xuất phát từ đỉnh $1$ của đồ thị, mỗi chu trình trên một dòng.

Sample Input

Sample Output:

1 2 1 3 4 1
1 2 1 4 3 1
1 2 3 1 4 1
1 2 3 5 4 1
1 2 4 1 3 1
1 2 4 5 3 1
1 3 1 2 4 1
1 3 1 4 2 1
1 3 2 1 4 1
1 3 4 1 2 1
1 3 5 4 2 1
1 4 1 2 3 1
1 4 1 3 2 1
1 4 2 1 3 1
1 4 3 1 2 1
1 4 5 3 2 1

2. Thiết kế giải thuật

Đến nay, vẫn chưa có thuật toán nào tốt hơn quay lui để tìm ra các chu trình Hamilton trên một đồ thị tổng quát. Cài đặt dưới đây sẽ tìm ra tất cả các chu trình Hamilton xuất phát từ đỉnh $1$ của đồ thị, các chu trình khác có thể thu được bằng cách hoán vị vòng quanh.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define task "Hamilton." using namespace std; const int maxn = 101; typedef int arr[maxn];
typedef int arr2[maxn][maxn]; // Nhập dữ liệu.
void enter(int &n, int &m, arr2 adj, arr deg)
{ cin >> n >> m; memset(adj, 0, sizeof(adj)); memset(deg, 0, sizeof(deg)); for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; ++adj[u][v]; ++adj[v][u]; ++deg[u]; ++deg[v]; }
} // Kiểm tra điều kiện đồ thị Hamilton.
bool check_hamilton_graph(int n, arr deg)
{ for (int u = 1; u <= n; ++u) if (deg[u] < 2) return false; return true;
} // In một chu trình Hamilton.
void print_hamilton_circuit(int n, arr circuit)
{ for (int i = 1; i <= n; ++i) cout << circuit[i] << ' '; cout << circuit[1] << endl;
} // Quay lui tìm các chu trình Hamilton.
void find_hamilton_circuit(int i, int n, arr2 adj, arr circuit, arr is_free)
{ // Thử chọn các đỉnh v kề với đỉnh liền trước trong chu trình và chưa thăm. for (int v = 1; v <= n; ++v) if (is_free[v] && adj[circuit[i - 1]][v]) { // Ghi nhận đỉnh v vào chu trình. circuit[i] = v; // Nếu chưa chọn đủ n đỉnh thì tiếp tục chọn. if (i < n) { // Đánh dấu đỉnh v đã chọn. is_free[v] = false; // Gọi đệ quy thử chọn đỉnh tiếp theo. find_hamilton_circuit(i + 1, n, adj, circuit, is_free); // Loại bỏ đỉnh v khỏi chu trình để thử trường hợp khác. is_free[v] = true; } // Đã chọn đủ n đỉnh và đỉnh thứ n tới được đỉnh 1 // Kết luận đã tìm được chu trình Hamilton. else if (adj[v][circuit[1]]) print_hamilton_circuit(n, circuit); }
} // Xử lý các trường hợp.
void solution(int n, arr2 adj, arr deg, arr is_free, arr circuit)
{ fill(is_free + 1, is_free + n + 1, 1); circuit[1] = 1; if (!check_hamilton_graph(n, deg)) cout << 0; else find_hamilton_circuit(2, n, adj, circuit, is_free);
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int n, m; arr2 adj; arr deg, is_free, circuit; enter(n, m, adj, deg); solution(n, adj, deg, is_free, circuit); return 0;
}

III. Tài liệu tham khảo

Đồ thị Hamilton và chu trình Hamilton

I. Tổng quan

II. Các khái niệm và định lý

Định lý 1

Định lý 2 (Định lý Dirak, 1952)

Định lý 3 (Định lý Ghouila - Houiri, 1960)

Định lý 4 (Định lý Ore, 1960)

Định lý 5 (Định lý Meynie, 1973)

Định lý 6 (Định lý Bondy - Chvátal, 1972)

III. Thuật toán tìm chu trình Hamilton

1. Phát biểu bài toán

2. Thiết kế giải thuật

Cài đặt

III. Tài liệu tham khảo

Bình luận

Bài viết tương tự

Thuật toán quay lui (Backtracking)

Các thuật toán cơ bản trong AI - Phân biệt Best First Search và Uniform Cost Search (UCS)

Sử dụng vector trong lập trình C++ - giải bài toán lập trình muôn thủa

MÔ PHỎNG THUẬT TOÁN VƯƠNG HẠO TRONG PROLOG

A* Search Algorithm

Python: Jump Search