Lời mở đầu

Gần đây, chúng ta đã chứng kiến sự phát triển chóng mặt của các mô hình sinh ảnh từ văn bản. Các mô hình như Mid-journey, Dall-e 3, Imagen, Stable Diffusion, StyleGAN-T,… có thể tạo ra những hình ảnh chân thực và sống động đến mức điên rồ.

Dù vậy, các mô hình đều có lượng thời gian suy diễn (hay sinh ảnh) rất lớn do cần lặp đi lặp lại quá trình khử nhiễu như ở các mô hình Diffusion. Các nghiên cứu gần đây ứng dụng quá trình chắt lọc tri thức (knowledge distillation) đã có thể giảm số bước xuống rất nhỏ (còn khoảng < 20 bước) để cho ra những bức ảnh có chất lượng tốt với mô hình Stable Diffusion tuy nhiên chưa từng có phương pháp được kiểm chứng đầy đủ nào có thể giảm số bước trong quá trình infer xuống chỉ còn “1 bước duy nhất”.

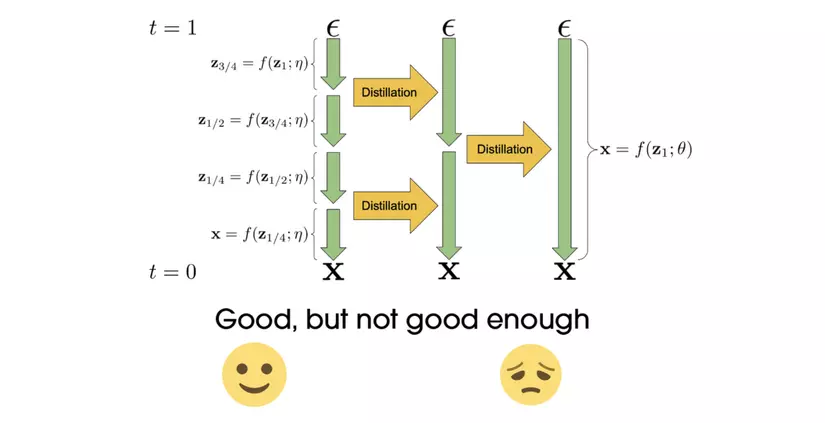
Hãy thử tưởng tượng từ một bức ảnh nhiễu, chúng ta có thể khử hoàn toàn trong một bước để sinh ra một bức ảnh có chất lượng tốt, điều đó có thể tiết kiệm cho chúng ta gấp nhiều lần thời gian khi muốn sinh ảnh từ văn bản. Nghe thật tuyệt đúng không nào?

Tuy nhiên khi ta cố giảm số step xuống một bước bằng quá trình chắt lọc tri thức, mô hình student học được cho ra kết quả vô cùng tệ. Điều này có thể lí giải bởi mô hình student chỉ có khả năng bắt chước mô hình SD teacher mà không có nhiều thông tin về mối liên hệ “có đôi có cặp” giữa ảnh nhiễu và ảnh gốc, cũng như quỹ đạo phức tạp mà ảnh nhiễu được vận chuyển (tạm hiểu rằng, mỗi khi ảnh nhiễu được khử nhiễu, nó đi được một bước nhỏ, qua nhiều bước liên tiếp như vậy nó sẽ vạch ra một quỹ đạo). Như ví dụ bên tay trái của ảnh phía dưới đây, quá trình distillation khiến cho kết quả vừa lẫn lộn, mờ và khó nhận ra được context của ảnh.

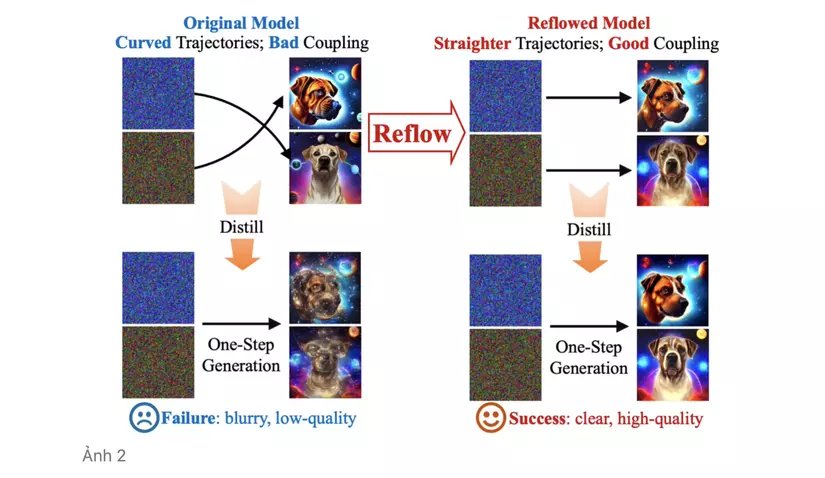InstaFlow là một mô hình được phát triển từ Stable Diffusion có khả năng giải quyết thách thức đó. Bằng cách “ghép cặp” đúng và hiệu quả các điểm dữ liệu thuộc 2 phân phối khác nhau trước khi áp dụng quá trình distillation, InstaFlow đã có thể “một bước lên mây” biến từ một ảnh nhiễu thành ảnh có chất lượng tốt, rõ ràng về nội dung. Vậy mô hình này đã sử dụng phép thuật gì hay ho ở đây? Hãy cùng mình đi sâu hơn về nó nhé!

Rectified flow và Reflow

Rectified flow

Mô hình luồng chỉnh lưu (Rectified Flow) là một chuỗi các biến đổi ánh xạ một điểm từ không gian này sang không gian khác hay từ một phân phối này sang phân phối khác (ví dụ như $\pi_0$ đến phân phối $\pi_1$).

❓ Cho trước các quan sát của 2 phân phối $\pi_0$ và $\pi_1$, tìm ánh xạ $T\colon\mathbb{R}^d\to\mathbb{R}^d$, thoả mãn $Z_1 := T(Z_0)\sim \pi_1$ khi $Z_0 \sim \pi_0$

Ví dụ trong quá trình sinh ảnh, $\pi_0$ thường là những phân phối đơn giản như phân phối gaussian và $\pi_1$ là phân phối của dữ liệu ảnh. Biết rằng $X_0 \sim \pi_0, X_1 \sim \pi_1$, dựa trên 2 quan sát này, Rectified Flows cố gắng học cách biến đổi dữ liệu $Z_0$ được lấy mẫu từ $\pi_0$ thành $Z_1$ thuộc phân phối $\pi_1$ tương ứng bằng phương trình vi phân thường (ODE- Ordinary Differential Equations) có dạng

$$\begin{align} \frac{dZ_t}{dt} = v(Z_t, t) \end{align}$$

Phương trình này có dạng thật quen đúng không nào, nếu ta xem $Z$ là quãng đường thì $v(Z_t,t)$ là vận tốc tức thời tại thời điểm t. Lúc này bài toán chúng ta đang giải là tìm ra con đường dẫn từ một địa điểm $Z_0$ đến $Z_1$ bằng cách đi từng bước nhỏ theo hướng của $v(Z_t,t)$. Hay ví dụ khác thể hiện rõ sự khác biệt về tính chất hay phân phối của các điểm dữ liệu: Tưởng tượng chúng ta đang muốn biến đổi một hình vuông 🟦 thành một hình tròn 🔵, ta có thể áp dụng một chuỗi các biến đổi nhỏ hơn ví dụ như từng bước gọt đi các góc nhọn của đa giác rồi cứ lặp lại như vậy cho đến khi hình thu được gần như tròn hoàn toàn.

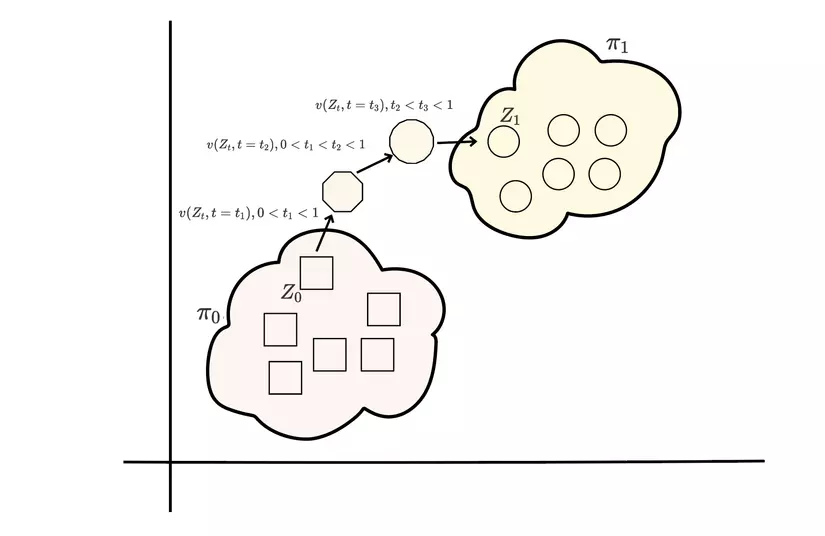
Oke, có thể bây giờ bạn đã hiểu rõ hơn về ODE, và bạn sẽ nhận ra đây vẫn là một bài toán khó nhằn! Một trong những cách để tìm ra $v$ chính là đi cực tiểu hoá khoảng cách giữa $\rho_1^v$ - phân phối của $Z_1$ khi đi theo luồng $v$ với phân phối $\pi_1$, ví dụ như phân kì KL (KL Divergence) $D_{KL}(\rho_1^v;~ \pi_1)$, tuy nhiên giống như có vô số con đường có thể đi giữa 2 điểm, cũng sẽ có vô số phương trình vi phân nên việc tính toán $\rho_1^v$ là hết sức tốn kém.

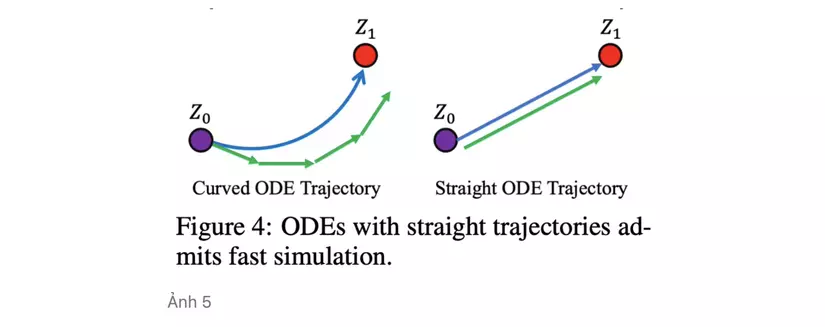
Tại sao lại được gọi là luồng chỉnh lưu? Vì Phương trình ODE cố gắng tối ưu vận chuyển từ phân phối $\pi_0$ đến $\pi_1$ theo một đường thẳng nhất có thể. Đường thẳng là giải pháp tối ưu hơn vì trên góc độ lí thuyết, đường thẳng là đường nối ngắn nhất giữa 2 điểm, và về mặt chính xác tính toán vì các điểm dữ liệu giữa 2 phân phối được vận chuyển theo đường cong thì không thể chính xác nếu ta rời rạc hoá theo thời gian so với đường thẳng.

Để làm được điều đó, trường vận tốc $v$ cần được chỉnh để “khớp” với chiều thẳng từ $X_0$ đến $X_1$ nhất có thể, đồng nghĩa với việc ta đi giải bài toán tối ưu

$$\begin{gather} \min _v \int_0^1 \mathbb{E}\left[\left\|\left(X_1-X_0\right)-v\left(X_t, t\right)\right\|^2\right] \mathrm{d} t, \text { với }X_t=t X_1+(1-t) X_0 \end{gather}$$

Bằng cách tham số hoá $v$ bằng một mạng neuron, ta có thể áp dụng SGD (Stochastic Gradient Descent) để tìm ra $v$!

Một vài giải thích thêm (skip nếu bạn không muốn đi quá sâu vào rectified flow nhé)

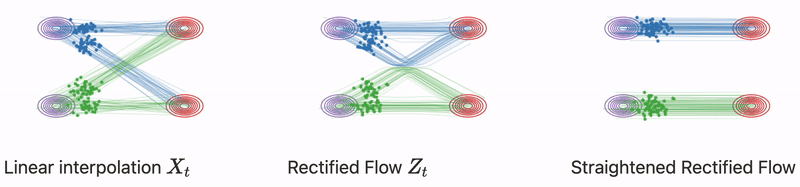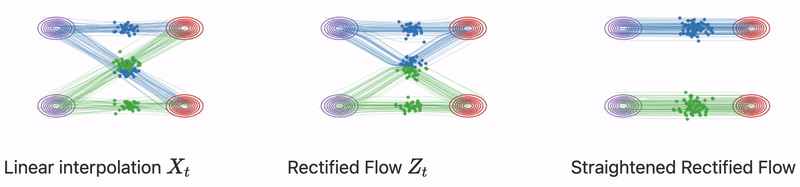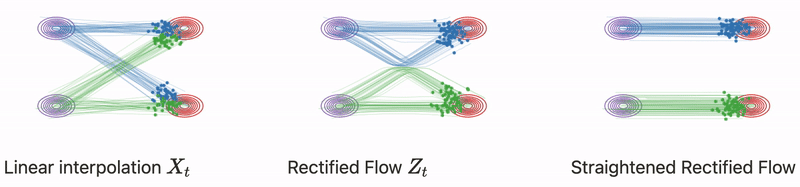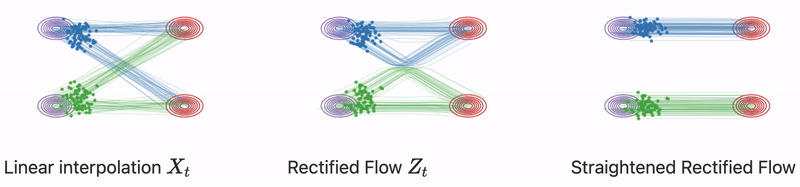
Từ từ đã, không phải nếu ta chọn một cách hoàn toàn tự nhiên phương trình vi phân có dạng

$$\begin{align} \mathrm{d}X_t = (X_1 - X_0) \mathrm{d}t, \end{align}$$

nghĩa là $X_t$ đi theo chiều $(X_1 - X_0)$ với vận tốc không đổi là đủ để giải quyết bài toán sao?

Trên thực tế với bất kì trạng thái $X_t$ nào, ta không thể biết được trạng thái cuối cùng $(X_1)$, việc tiếp tục update $X_t$ chỉ phụ thuộc vào giá trị hiện tại và trước đó (khái niệm này còn gọi là causual) ví dụ trong quá trình denoise một bức ảnh nhiễu, ta đâu thể biết được đích đến mà chỉ biết được trạng thái nhiễu hiện tại và trước đó của ảnh. Và khi nhiều quỹ đạo chuyển động có thể giao nhau như hình trên, chuyển động của điểm dữ liệu có thể đi theo nhiều hướng để đến được phân phối $\pi_1$ điều này là không đúng với phương trình vi phân đã đề ra từ đầu $\frac{dZ_t}{dt} = v(Z_t, t)$. Bạn cũng có thể tìm hiểu thêm về (”A uniqueness criterion for ordinary differential equations”).

Việc giải bài toán tối ưu như ở công thức (2) có thể được giải thích bởi 2 tính chất quan trọng mà rectified flow có thể đảm bảo:

• $Z_0, Z_1$ có cùng xác suất biên với $X_0, X_1$ cũng có nghĩa chúng cũng là một cặp dữ liệu của 2 phân phối $X_0, X_1$.

  

• Với bất kì hàm lồi $c: R^d \rightarrow R$ nào $\mathbb{E}[c(Z_1 - Z_0)] \leq \mathbb{E}[c(X_1 - X_0)]$ (chi phí vận chuyển giữa $Z_0, Z_1$ nhỏ hơn hoặc bằng chi phí vận chuyển của $X_0, X_1$.

Về phần chứng minh, bạn đọc có thể tham khảo thêm tại đây

Reflow

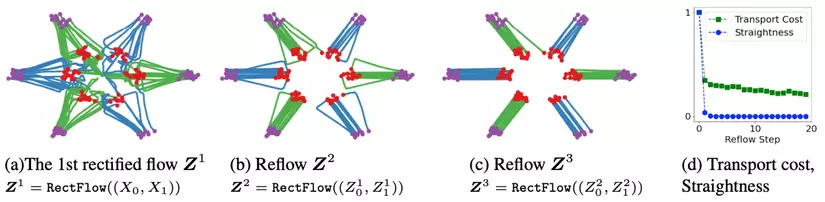
Liệu chúng ta chỉ cần áp dụng rectified flow 1 lần là đủ?

Câu trả lời là không!

Như minh hoạ trên ảnh 6, ta có thể dễ dàng nhận ra rằng luồng vận chuyển giữa các điểm trong vẫn rất phức tạp và tốn kém sau quá trình chỉnh lưu đầu tiên. Để tối ưu hơn nữa về chi phí vận chuyển, ta nghĩ đến việc lặp đi lặp lại tác dụng của rectified flow.

Giả sử $\boldsymbol Z = \{Z_t: t\in[0,1]\}$ là rectified flow thu được từ cặp quan sát $(X_0,X_1)$, khi đó $\boldsymbol Z = \mathsf{Rectflow}((X_0,X_1))$. Reflow thực chất là thực hiện đệ quy quá trình trên

$$\boldsymbol Z^{k+1} = \mathsf{Rectflow}((Z_0^k, Z_1^k))$$

hay

$$\begin{align} \begin{gathered}v_{k+1}=\underset{v}{\arg \min } \mathbb{E}_{X_0 \sim \pi_0}\left[\int_0^1\left\|\left(X_1-X_0\right)-v\left(X_t, t\right)\right\|^2 \mathrm{~d} t\right] \text {, } \\\text { với } X_1=\mathrm{ODE}\left[v_k\right]\left(X_0\right) \text { và } X_t=t X_1+(1-t) X_0\end{gathered} \end{align}$$

(Phần giải thích chi tiết thuật toán ngay dưới đây sẽ giúp các bạn hiểu hơn nên đừng lo nếu chưa hiểu rõ nhé!)

Thực tế dựa trên hình d, kể cả số lượng reflow cần thiết là rất nhỏ cũng đủ để giảm chi phí vận chuyển đi rất rất nhiều lần!

Text-Conditioned Reflow

Việc bổ sung text prompt hoàn toàn đơn giản bằng cách điều chỉnh công thức với text prompt là điều kiện cho trước

$$\begin{align} \begin{gathered} v_{k+1}=\underset{v}{\arg \min } \mathbb{E}_{X_0 \sim \pi_0, \mathcal{T} \sim D_{\mathcal{T}}}\left[\int_0^1\left\|\left(X_1-X_0\right)-v\left(X_t, t \mid \mathcal{T}\right)\right\|^2 \mathrm{~d} t\right] \\ \text { với } X_1=\operatorname{ODE}\left[v_k\right]\left(X_0 \mid \mathcal{T}\right) \text { và } X_t=t X_1+(1-t) X_0 \end{gathered} \end{align}$$

Trong paper Instaflow, người ta lấy luôn một luồng có sẵn được huấn luyện từ trước với k=0 (giai đoạn khởi tạo) và áp dụng quá trình reflow trên luồng cho trước này, thuật toán đầy đủ như sau:

Để giải thích kĩ càng hơn về thuật toán, chúng ta sẽ đi vào từng phần:

• Ở giai đoạn khởi tạo, chúng ta có thể chọn mô hình được huấn luyện từ trước, cụ thể ở đây là mô hình Stable Diffusion - một mô hình đã có khả năng sinh ảnh khá tốt từ văn bản, tuy nhiên, quỹ đạo khi ảnh đi từ nhiễu đến một bức ảnh rõ ràng đang rất ngẫu nhiên và mục tiêu của chúng ta là khiến nó trở thành thẳng hơn

• Tiếp theo, lấy mẫu $X_0, X_1$ từ $\pi_0 × \pi_1$ (dựa trên text prompt $\tau$ bằng Stable Diffusion), huấn luyện mạng khử nhiễu bằng cách tối thiểu

  $$\begin{align} \mathbb{E}_{X_0 \sim \pi_0, \mathcal{T} \sim D_{\mathcal{T}}}\left[\int_0^1\left\|\left(X_1-X_0\right)-v\left(X_t, t \mid \mathcal{T}\right)\right\|^2 \mathrm{~d} t\right] \end{align}$$

  ta thu được luồng chỉnh lưu đầu tiên. Lặp lại quá trình trên (reflow) bằng một số lượt được xác định trước (user-defined upper bound). Một lưu ý nhỏ ở đây là sau bước đầu tiên, $X_0, X_1$ ở bước thứ $k+1$ cần được sinh ra từ mô hình ở bước ngay trước nó (bước thứ $k$)

Khi quá trình trích suất tri thức vào cuộc!

Tuyệt! đến đây, bằng cách huấn luyện ra $v_k$, ta có thể tìm ra “con đường” để đi từ một phân phối nhiễu đến phân phối dữ liệu ảnh. Tuy nhiên, câu chuyện vẫn chưa dừng lại ở đây. Bằng quá trình chắt lọc tri thức, ta mong muốn học ra một mạng nơ-ron đơn giản hơn mạng $v_k$ là mạng nơ-ron student $\tilde{v}_k$

$$\begin{align} \tilde{v}_k=\underset{v}{\arg \min } \mathbb{E}_{X_0 \sim \pi_0, \mathcal{T} \sim D_{\mathcal{T}}}\left[\mathbb{D}\left(\mathrm{ODE}\left[v_k\right]\left(X_0 \mid \mathcal{T}\right), \quad X_0+v\left(X_0 \mid \mathcal{T}\right)\right)\right] \end{align}$$

Thuật toán đầy đủ để tìm $\tilde{v}_k$ được mô tả chi tiết dưới đây

Để hiểu kĩ hơn về knowledge distillation, các bạn có thể tham khảo bài báo sau

PROGRESSIVE DISTILLATION FOR FAST SAMPLING OF DIFFUSION MODELS

Một vài quan sát từ thực nghiệm

Như đã đặt vấn đề ngay từ đầu, việc sử dụng quá trình reflow là bước quan trọng để đảm bảo rằng đường đi hoặc quỹ đạo của luồng vận chuyển đã được điều chỉnh đủ thẳng. Điều này là cần thiết khi chúng ta muốn áp dụng các kỹ thuật chắt lọc tri thức

• Mô hình Stable Diffusion đóng vai trò teacher bỏ xa mô hình student về chỉ số FID (Fréchet inception distance), cũng như ảnh sinh ra bởi mô hình student có sai khác lớn và không rõ về nội dung
• Dù cho mô hình SD gốc và sau khi được áp dụng 2 lần reflow có chỉ số FID là xấp xỉ như nhau, sau quá trình chắt lọc tri thức, mô hình 2-rectified flow có kết quả tốt hơn hẳn mô hình SD gốc, cũng có nghĩa là khoảng cách giữa mô hình student và teacher được giảm đi đáng kể nhờ vào reflow. Chất lượng ảnh sinh ra quan sát được có tính tương đồng cao so với ảnh gốc và trực quan, dễ nhìn (nói chung là xinh đẹp không thua gì bản gốc=))

$$\begin{align} S(Z)=\int_{t=0}^1 \mathbb{E}\left[\left\|\left(Z_1-Z_0\right)-v\left(Z_t, t\right)\right\|^2\right] \mathrm{d} t \end{align}$$

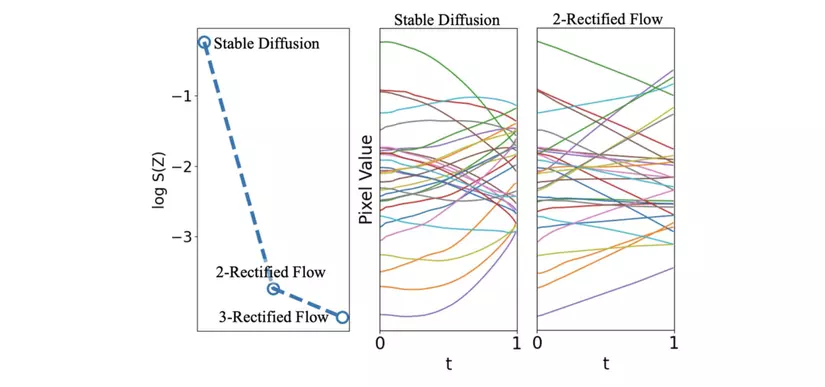
$S(Z) = 0$ nghĩa là quỹ đạo vạch ra bởi ODE hoàn toàn thẳng. Ảnh [8] cho ta thấy rõ được tác dụng của quá trình reflow mạnh mẽ như thế nào trong việc “nắn thẳng” đường vận chuyển, các pixel được biến đổi bởi mô hình Stable Diffusion chủ yếu di chuyển theo các đường cong trong nhưng sau 2 bước reflow đã có thể di chuyển theo các đường gần như thẳng tắp

Dưới đây là một số kết quả định lượng khác về Inference Time và FID

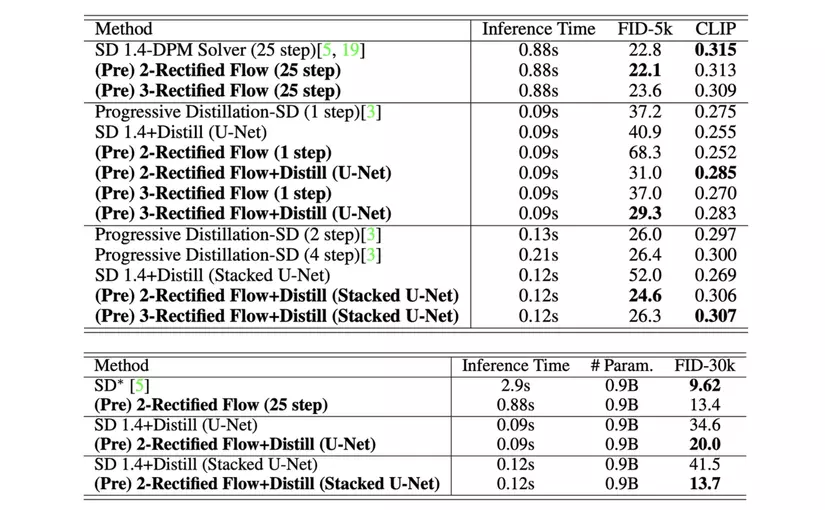
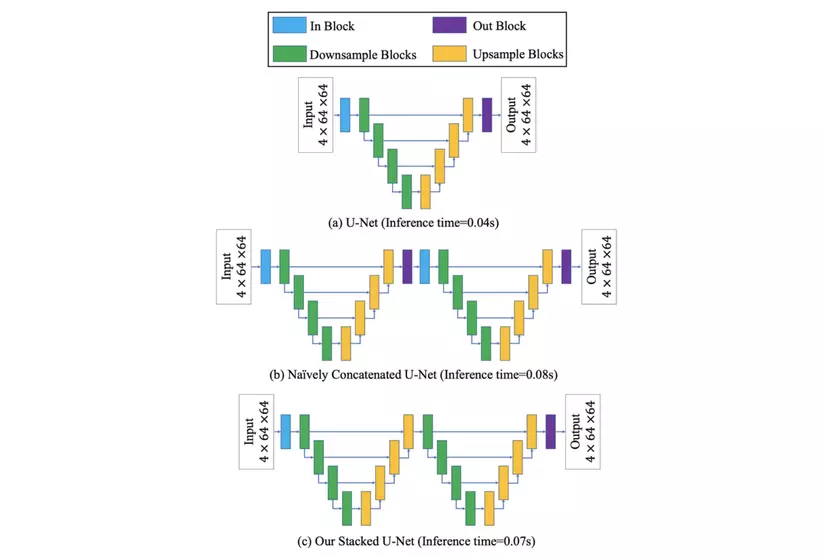
Một điều khá hay ho trong quá trình thử nghiệm đó là ngoài sử dụng U-Net là mô hình học sinh trong quá trình chiết xuất tri thức, người ta sử dụng thêm một kiến trúc mô hình khác là Stacked U-Net, một phiên bản đơn giản hoá của việc ghép nối liên tiếp hai mạng U-Net thông thường bằng cách bỏ qua out block (màu tím) và in block (màu xanh) trung gian. Về mặt thời gian, quá trình infer có thể lâu hơn U-Net nhưng lại tối ưu hơn 2 U-Net nối tiếp, bù lại, hiệu năng lại được tăng lên đáng kể (thời gian suy diễn nhanh gấp hơn 20 lần SD thông thường, chỉ số FID đạt 13.7 trên tập MS COCO 2014 với 30, 000 ảnh).

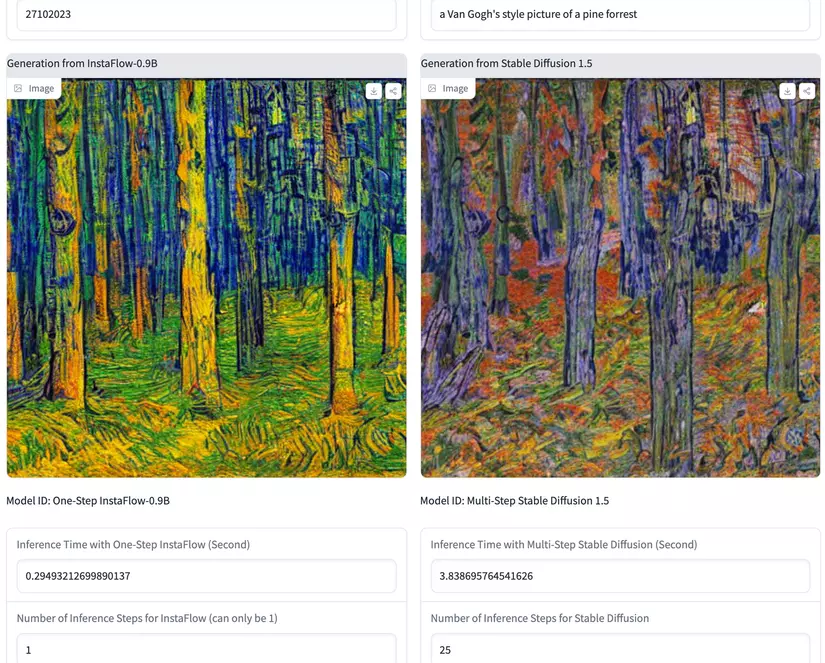
Dưới đây là một số so sánh về chất lượng ảnh sinh bởi InstaFlow (1 bước) và SD 1.5-DPM Solver (25 bước) với cùng một văn bản Quá là tuyệt vời, bạn đọc cũng có thể tự mình thử sinh một vài bức ảnh và so sánh tại

https://huggingface.co/spaces/XCLiu/InstaFlow

Kết luận

Tóm lại bức tranh toàn cảnh về InstaFlow và những gì mình đã giải thích đến bây giờ có thể được minh hoạ bởi hình ảnh dưới đây:

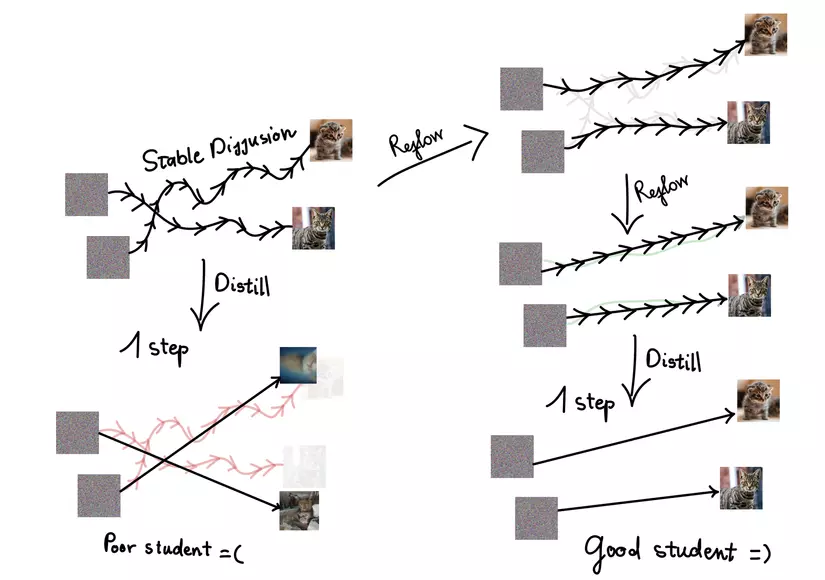
Kỹ thuật reflow giúp làm thẳng đường đi của các luồng xác suất, cải thiện sự liên kết giữa nhiễu và hình ảnh, tạo điều kiện cho quá trình chưng cất diễn ra thành công và giúp mô hình Stable Diffusion tạo ra hình ảnh chất lượng cao chỉ trong một bước. InstaFlow mở ra một bước tiến lớn cho mô hình Diffusion nói chung và các mô hình sinh ảnh dựa trên văn bản Text2Image nói riêng. Cải tiến InstaFlow như thế nào? Fine-tuning mô hình sinh một bước này ra sao? Liệu có thể thay thế kiến trúc U-Net bằng một kiến trúc mạnh mẽ hơn? Đó là những thách thức mà mình và các bạn có thể cùng nhau đi sâu hơn trong tương lai!

References:

• InstaFlow: One Step is Enough for High-Quality Diffusion-Based Text-to-Image Generation
• Rectified Flow: A Marginal Preserving Approach to Optimal Transport
• Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow
• PROGRESSIVE DISTILLATION FOR FAST SAMPLING OF DIFFUSION MODELS
• DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps
• https://www.cs.utexas.edu/~lqiang/rectflow/html/intro.html#equation-equ-dzvtdt
• https://phamdinhkhanh.github.io/2021/03/13/KnownledgeDistillation.html
• https://www.sciencedirect.com/topics/engineering/causal-system

🔗 Tìm hiểu về Pixta Vietnam

Cập nhật tin tức mới nhất của Pixta Vietnam 👉 http://bit.ly/3kdkzvW