Nhiều vấn đề lập trình có thể được giải quyết bằng cách mô hình hóa vấn đề dưới dạng đồ thị và sử dụng thuật toán đồ thị phù hợp. Một số ví dụ điển hình về đồ thị là mạng lưới đường bộ và thành phố trong 1 quốc gia. Tuy nhiên, đôi khi, không phải vấn đề nào cũng dễ dàng nhìn ra để triển khai đồ thị và giải quyết. Đó là lý do tôi viết về những khái niệm cơ bản trong đồ thị và các thuật toán thường dùng để giúp ta có thể phát hiện và triển khai thuật toán đồ thị trong nhưng vấn đề liên quan. Ở phần I này ta tập trung vào hiểu các thuật ngữ sử dụng trong Đồ Thị. (Graph)

Thuật ngữ về Đồ Thị.

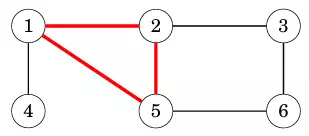
Một đồ thị (Graph) bao gồm các nút (node) và các cạnh (edges). Trong series này tôi dùng biến n đại diện cho n nút, và biến m đại diện cho m cạnh. Các nút được đánh số từ 1, 2, ..., n. Ví dụ đồ thị sau bao gồm 5 nút và 7 cạnh .

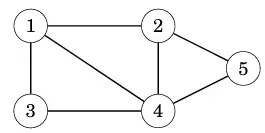
Đường dẫn (Path) từ nút a đến nút b qua các cạnh của đồ thị . Đồ dài của 1 đường dẫn là tổng số cạnh trong nó. Ví dụ ở hính dưới, ta có thể thấy đồ thị bao gồm 1 đường dẫn 1 -> 3 -> 4 -> 5 (in đỏ) có chiều dài là 3 (3 cạnh) nối từ nút 1 đến nút 5.

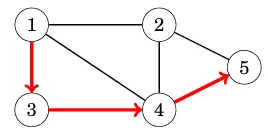
Một đường dẫn được coi là chu kỳ (cycle) nếu nút đầu tiên và nút cuối giống nhau (tức tạo thành 1 vòng kín).

Ví dụ, đồ thị ở trên chứa 1 chu kỳ 1 -> 3 -> 4 -> 1.

Khái niệm liên thông (Connectivity)

Một đồ thị liên thông nếu 2 nút bất kì trong đồ thị tồn tại đường dẫn giữa 2 nút đó. Ví dụ đồ thị bên dưới được gọi là liên thông:

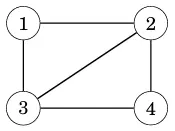
Với đồ thị trên ta thấy nó là 1 đồ thị liên thông vì luôn tồn tại 1 đường dẫn nối 2 điểm trong nó.

Ví dụ về 1 đồ thị khôn liên thông ở hình bên dưới, ta thấy không có cách nào, hay không có đường dẫn nào từ 3 nút còn lại đến được với nút 4.

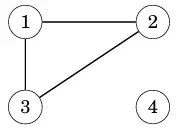
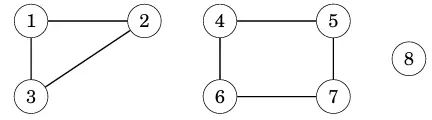
Một đường dẫn liên thông của 1 đồ thị thì được gọi là 1 thành phần liên thông (components). Ví dụ ở dưới ta có thể thấy, đồ thị bao gồm 3 thành phần liên thông là {1, 2, 3}; {4, 5, 6, 7} và {8}

Tiếp theo chúng ta sẽ tìm hiểu về cây (a tree), cây cũng là 1 đồ thị liên thông có n nút với n - 1 cạnh. Một số lưu ý về cây:

• Chỉ tồn tại duy nhất 1 đường dẫn nối 2 nút bất kì trên cây. Hiểu đơn giản thì cây không bao gồm chu kì trong nó, đó là lý do tại sao cây n nút thì chỉ có n - 1 cạnh vì nếu nhiều hơn sẽ sinh ra chu kì, có thể tìm chứng minh ở trên Google.

Ví dụ bên dưới về cây:

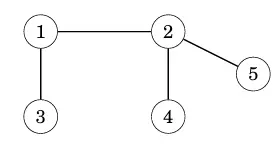
Đồ thị có hướng (Directions)

Một đồ thị có hướng nếu các cạnh chỉ có thể đi qua theo một hướng. Ví dụ, đồ thị sau đây được gọi là đồ thị có hướng:

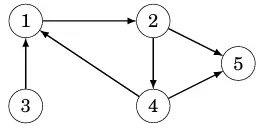
Đồ thị trên chứa đường dẫn 3 -> 1 -> 2 -> 5 từ nút 3 đến nút 5, nhưng không có đường dẫn nào đi ngược lại từ nút 5 về nút 3.

Đồ thị có trọng số (Weights)

Một đồ thị được gọi là đồ thị có trọng số nếu mỗi cạnh được đi kèm với một trọng số. Các trọng số thường được diễn giải là độ dài của cạnh hoặc chi phí đi qua cạnh đấy. Ví dụ, đồ thị sau được gọi là đồ thị có trọng số:

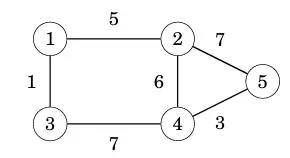
Tổng chi phí hay độ dài của 1 đường dẫn trong đồ thị có trọng số là tổng trọng số của các cạnh trên đường dẫn đó. Ví dụ trong đồ thị trên, độ dài của đường dẫn 1 -> 2 -> 5 là 12 và độ dài của đường dẫn 1 -> 3 -> 4 -> 5 là 11 (Đường dẫn này chính là đường dẫn ngắn nhất đi từ nút 1 đến nút 5)

Hàng xóm và Bậc của nút (Neighbors || Adjacent && Degree)

Hai nút được gọi là hàng xóm (Neighbors) hay kề (Adjacent) nếu có 1 cạnh giữa chúng.

Bậc (Degree) của một nút là số lượng nút kề của nút đó (hay số lượng hàng xóm bao quanh nút đó).

Ví dụ, trong đồ thị sau, hàng xóm hay nút kề của nút 2 là 1, 4 và 5, do đó bậc của nút 2 là 3.

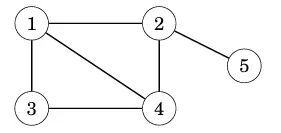
Tổng các bậc trong một đồ thị luôn là 2m, trong đó m là số cạnh, vì mỗi cạnh tăng bậc của đúng 2 nút lên một. Vì lý do này, tổng các bậc luôn là số chẵn.

Một đồ thị được gọi là đồ thị chính quy (hay đồ thị đều) (Regular Graph) nếu bậc của tất cả các nút đều bằng nhau.

Một đồ thị được gọi là đồ thị đầy đủ (Complete Graph) nếu đồ thị đó có n nút mà bậc của mỗi nút là n - 1, tức là đồ thị chứa tất cả các cạnh có thể có giữa các nút.

Trong đồ thị có hướng, bậc vào (indegree) của một nút là số cạnh kết thúc tại nút, và bậc ra (outdegree) của một nút là số cạnh bắt đầu đó tại nút đó. Ví dụ đồ thị bên dưới, bậc vào của nút 2 là 2 (cạnh từ 1 -> 2, cạnh từ 5 -> 2), và bậc ra của nút 2 là 1 (cạnh từ 2 -> 4)

Tô màu đồ thị (Coloring)

Trong quá trình tô màu đồ thị, mỗi nút được gán một màu sao cho không có nút kề nhau nào có cùng màu.

Một đồ thị gọi là đồ thị 2 phần (bipartite) nếu có thể tô 2 màu cho đồ thị đó.

Mẹo nhỏ: Một đồ thị là đồ thị 2 phần chính xác khi nó không chứa một chu trình có số cạnh lẻ.

Ví dụ đồ thị sau:

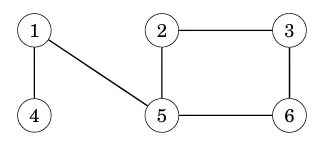
Nó là 1 đồ thị 2 phần bởi vì ta có thể tô màu theo dạng sau:

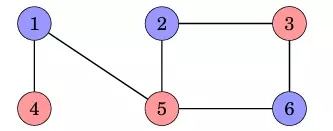
Trường hợp đồ thị bên dưới không phải là đồ thị 2 phần:

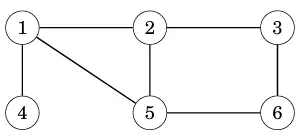
Bởi vì nó thể tô màu với 2 màu như lý thuyết ở trên, ta thấy tồn tại 1 chu kì 3 cạnh {1, 2, 5}

Tính đơn giản (Simplicity)

Đồ thị được coi là đồ thị đơn nếu trong đồ thị không tồn tại cạnh nào vừa bắt đầu và vừa kết thúc tại một nút, và không nó nhiều cạnh giữa 2 nút.

Ví dụ dưới đây không phải đồ thị đơn:

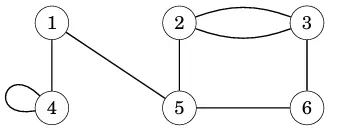
Dưới đây là độ thị đơn:

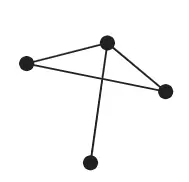
Một vài cách để biểu diễn đồ thị.

Có một số cách để biểu diễn đồ thị trong thuật toán. Việc lựa chọn cấu trúc dữ liệu phụ thuộc vào kích thước của đồ thị và cách thuật toán xử lý nó. Tiếp theo chúng ta sẽ xem xét ba cách biểu diễn phổ biến.

Biểu diễn dưới dạng danh sách kề. (Adjacency list representation)

Trong biểu diễn danh sách kề, mỗi nút x trong đồ thị gán một danh sách kề bao gồm các nút có cạnh từ x đến nó.

Danh sách kề là cách phổ biến nhất để biểu diễn đồ thị và hầu hết các thuật toán có thể được triển khai hiệu quả bằng cách sử dụng chúng.

Một cách thuận tiện để sử dụng danh sách kề là khai báo 1 vector như sau:

vector<int> adj(n);

Hằng số N được chọn để tất cả các danh sách kề có thể được lưu trữ. Ví dụ, đồ thị sau:

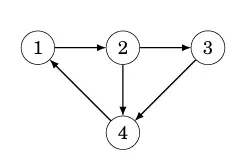
có thể được lưu trữ như sau:

adj[1].push_back(2);
adj[2].push_back(3);
adj[2].push_back(4);
adj[3].push_back(4);
adj[4].push_back(1);

Với đồ thị vô hướng, nó có thể được lưu trữ theo cách tương tự, nhưng mỗi cạnh được them vào theo cả 2 hướng.

Đối với đồ thị có trọng số, cấu trúc có thể được mở rộng như sau:

vector<pair<int, int>> adj(n);

Trong trường hợp này, danh sách kề của nút a chứa cặp {b, w}, hàm ý có cạnh từ nút a đến nút b với trọng số w

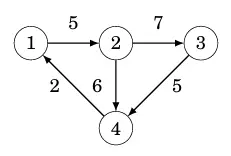
có thể được lưu trữ như sau:

adj[1].push_back({2, 5});
adj[1].push_back({3, 7});
adj[1].push_back({4, 6});
adj[1].push_back({4, 5});
adj[1].push_back({1, 2});

Lợi ích của việc sử dụng danh sách kề là chúng ta có thể tìm thấy hiệu quả các nút mà chúng ta có thể di chuyển từ một nút nhất định thông qua một cạnh. Ví dụ, vòng lặp sau đây sẽ đi qua tất cả các nút mà chúng ta có thể di chuyển từ nút s.

for(auto u : adj[s]) { // process node u
}

Biểu diễn thông qua ma trận kề (Adjacency matrix representation)

Ma trận kề là một mảng hai chiều cho biết đồ thị chứa những cạnh nào. Chúng ta có thể kiểm tra hiệu quả từ ma trận kề xem có một cạnh giữa hai nút hay không. Ma trận có thể được lưu trữ dưới dạng một mảng

vector<vector<int>> adj(n, vector<int> (n, 0));
// int adj[N][N]

Trong đó mỗi giá trị adj[a][b] cho biết đồ thị có chứa cạnh từ nút a đến nút b hay không. Nếu cạnh được bao gồm trong đồ thị, thì adj[a][b] = 1, và nếu không thì adj[a][b] = 0. Ví dụ, đồ thị:

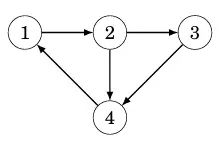
có thể được biểu diễn:

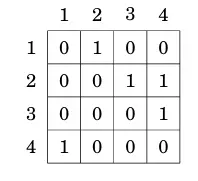
Nếu đồ thị có trọng số, biểu diễn ma trận kề có thể được mở rộng để ma trận chứa trọng số của cạnh nếu cạnh đó tồn tại. Ví dụ, đồ thị

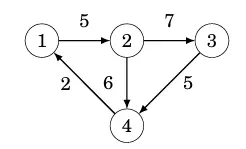
có thể biểu diễn bởi ma trận tương ứng

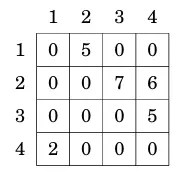
Nhược điểm của biểu diễn ma trận kề là ma trận chứa n^2 phần tử và thường thì hầu hết chúng đều bằng không. Vì lý do này, không thể sử dụng biểu diễn nếu đồ thị lớn.

Biểu diễn danh sách cạnh (Edge list representation)

Danh sách cạnh chứa tất cả các cạnh của đồ thị theo một thứ tự nào đó. Đây là một cách thuận tiện để biểu diễn đồ thị nếu thuật toán xử lý tất cả các cạnh của đồ thị và không cần phải tìm các cạnh bắt đầu tại một nút nhất định. Danh sách cạnh có thể được lưu trữ trong một vectơ

vector<pair<int, int>> edges;

Trong đó mỗi cặp {a, b} biểu thị rằng có một cạnh từ nút a đến nút b. Đó đó, đồ thị sau:

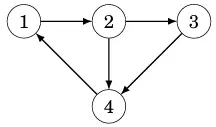
có thể biểu diễn như sau

edges.push_back({1,2});
edges.push_back({2,3});
edges.push_back({2,4});
edges.push_back({3,4});
edges.push_back({4,1});

Nếu đồ thị được cân nhắc, cấu trúc có thể được mở rộng như sau:

vector<tuple<int, int, int>> edges;

Mỗi phần tử trong danh sách này có dạng (a,b,w), nghĩa là có một cạnh từ nút a đến nút b có trọng số w. Ví dụ, đồ thị:

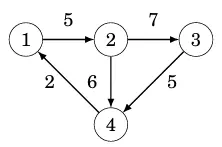
có thể được biểu diễn như sau:

edges.push_back({1,2,5});
edges.push_back({2,3,7});
edges.push_back({2,4,6});
edges.push_back({3,4,5});
edges.push_back({4,1,2});