I. Cây DFS và bài toán định chiều đồ thị

1. Phân loại các cung trên cây $\text{DFS}$

Trong quá trình $\text{DFS}$ duyệt đồ thị, với mỗi đỉnh $u$ ta có được đỉnh $\text{par}[u]$ là đỉnh cha của đỉnh $u$ trên đường đi. Nếu xây dựng đồ thị con gồm các cạnh có dạng $(\text{par}[u], u),$ ta sẽ thu được một cây, gọi là cây $\text{DFS}$. Hình vẽ dưới đây biểu diễn một cây $\text{DFS}$ với $9$ đỉnh, các cạnh nét liền là cạnh thuộc cây $\text{DFS}$, các cạnh nét đứt là cạnh không thuộc cây $\text{DFS}$.

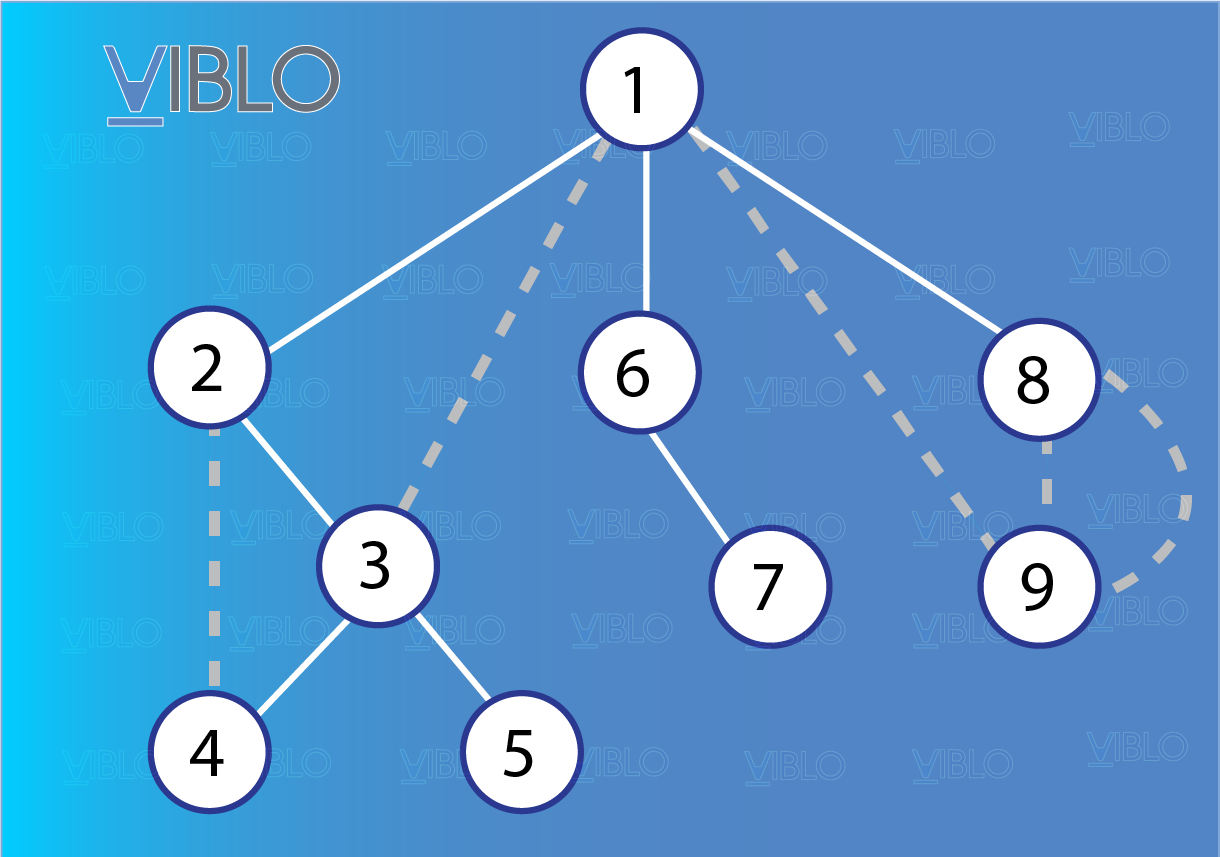
Trên đồ thị có hướng, xét mọi cung được thăm và không được thăm trong quá trình $\text{DFS},$ ta có các loại cung sau:

• Cung của cây DFS (Tree Edges): Các cung được thăm trong quá trình $\text{DFS}$ (cung màu trắng nét liền).
• Cung xuôi (Forward edges): Cung không thuộc cây $\text{DFS}$ có dạng $(u \rightarrow v)$; trong đó $u$ là cha của $v$ trong quá trình $\text{DFS}$ (cạnh xanh lá).
• Cung ngược (Back edges): Cung không thuộc cây $\text{DFS}$ và có dạng $(v \rightarrow u)$; trong đó $u$ là cha của $v$ (cạnh đỏ) nhưng $v$ đã được thăm trước đó do một dây chuyền $\text{DFS}$ khác.
• Cung chéo (Cross edges): Cung không thuộc cây $\text{DFS}$, trong đó $u$ và $v$ thuộc hai nhánh khác nhau của cùng một cây $\text{DFS}$ (cạnh tím). Cung này sinh ra do tồn tại một đỉnh $w$ đã duyệt trước cả $u$ và $v$, và đỉnh $w$ này tạo ra hai nhánh $\text{DFS}$ khác nhau, một nhánh chứa $u$ và một nhánh chứa $v$. Cung chéo chỉ có thể đi từ nhánh thăm sau tới nhánh thăm trước chứ không thể đi từ nhánh thăm trước tới nhánh sau trước (thật vậy, nếu cung chéo đi từ nhánh thăm trước sang nhánh thăm sau thì cung đó cũng chính là cung thuộc nhánh thăm trước).

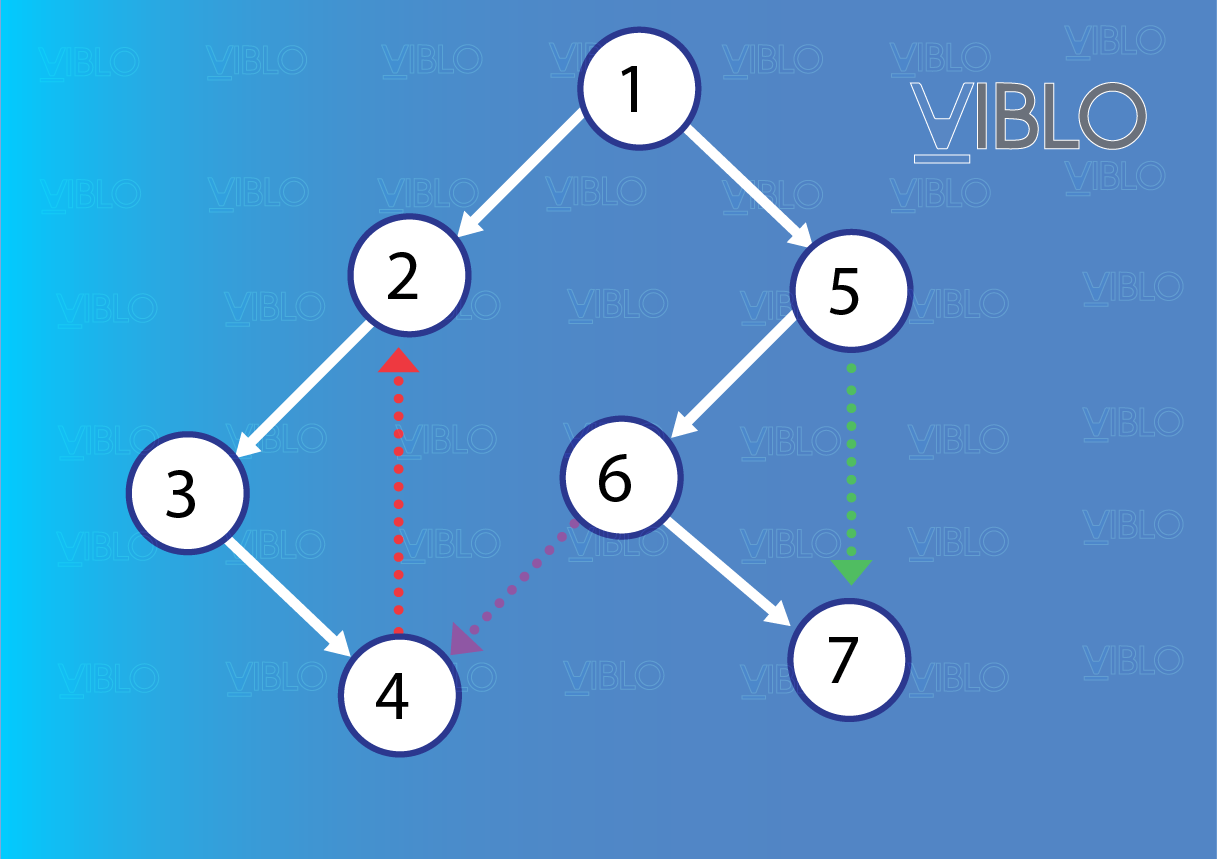
Trên đồ thị vô hướng, chỉ tồn tại hai loại cung là cung thuộc cây $\text{DFS}$ và cung ngược (không thuộc cây $\text{DFS}$).

Đối với đồ thị vô hướng, nếu như trong quá trình $\text{DFS}$, cứ khi duyệt qua một cạnh $(u, v)$ thì ta bỏ luôn chiều $(v, u)$ đi và định chiều lại cạnh $(u, v)$ thành cung $(u \rightarrow v)$, thì thu được một phép định chiều đồ thị gọi là phép định chiều $\text{DFS}$.

2. Đánh số các đỉnh trên cây $\text{DFS}$ và ghi nhận cung ngược lên cao nhất

Một số định nghĩa mảng sử dụng:

• $\text{num}[u]:$ Số thứ tự duyệt đến của đỉnh $u$ trong quá trình $\text{DFS}$.
• $\text{low}[u]:$ Số thứ tự nhỏ nhất (giá trị $\text{num}[]$) của một đỉnh $v$ tới được từ nhánh $\text{DFS}$ gốc $u$ bằng tối đa một cung ngược. Có nghĩa là, nếu trong nhánh $\text{DFS}$ gốc $u$ tồn tại nhiều cung ngược, thì ta ghi nhận cung ngược hướng lên đỉnh có thứ tự thăm nhỏ nhất. Ban đầu $\text{low}[u] = \text{num}[u],$ do đỉnh $u$ có thể tự đi tới chính nó.
• $\text{par}[u]:$ Đỉnh cha của đỉnh $u$ trên cây $\text{DFS}$.
• $\text{tail}[u]:$ Thời điểm duyệt xong nhánh $\text{DFS}$ gốc $u$. Các đỉnh có số thứ tự thăm từ $\text{num}[u]$ tới $\text{tail}[u]$ sẽ thuộc nhánh $\text{DFS}$ gốc $u$.

Nhận xét: Trong quá trình $\text{DFS}$ từ đỉnh $u$ tới đỉnh $v,$ xảy ra ba trường hợp:

• Nếu đỉnh $v$ chính bằng đỉnh đã gọi đệ quy tới $u$ ở trước đó thì bỏ qua.
• Nếu đỉnh $v$ chưa thăm thì $\text{DFS}$ thăm $v$. Khi duyệt xong nhánh $\text{DFS}$ gốc $v,$ ta đã xây dựng được một nhánh $\text{DFS}$ gốc $v$ là cây con của nhánh $\text{DFS}$ gốc $u$. Do đó, các cung ngược đi ra từ nhánh $\text{DFS}$ gốc $v$ cũng là cung ngược đi ra từ nhánh $\text{DFS}$ gốc $u$. Ta sẽ cực tiểu hóa:

$$\text{low}[u] = \text{min}(\text{low}[u], \text{low}[v])$$

• Nếu đỉnh $v$ đã thăm rồi, tức là $(u \rightarrow v)$ là một cung ngược không thuộc cây $\text{DFS}$. Ta cực tiểu hóa:

$$\text{low}[u]=\text{min}(\text{low}[u], \text{num}[v])$$

Cài đặt:

int time_dfs = 0; void dfs(int u)
{ num[u] = low[u] = ++time_dfs; // Xác định thời điểm duyệt tới của đỉnh u. for (int v: adj[u]) { if (v == par[u]) // Đỉnh v là đỉnh cha của đỉnh u -> bỏ qua. continue; if (!num[v]) // Chưa duyệt v. { par[v] = u; // Gán cha của đỉnh v là đỉnh u. dfs(v); low[u] = min(low[u], low[v]); // Cực tiểu hóa low[u]. } else // Đỉnh v đã duyệt qua, (u -> v) là cung ngược.  { low[u] = min(low[u], num[v]); } } tail[u] = time_dfs;
}

Hình vẽ dưới đây minh họa một đồ thị gồm $8$ đỉnh và các cạnh của nó:

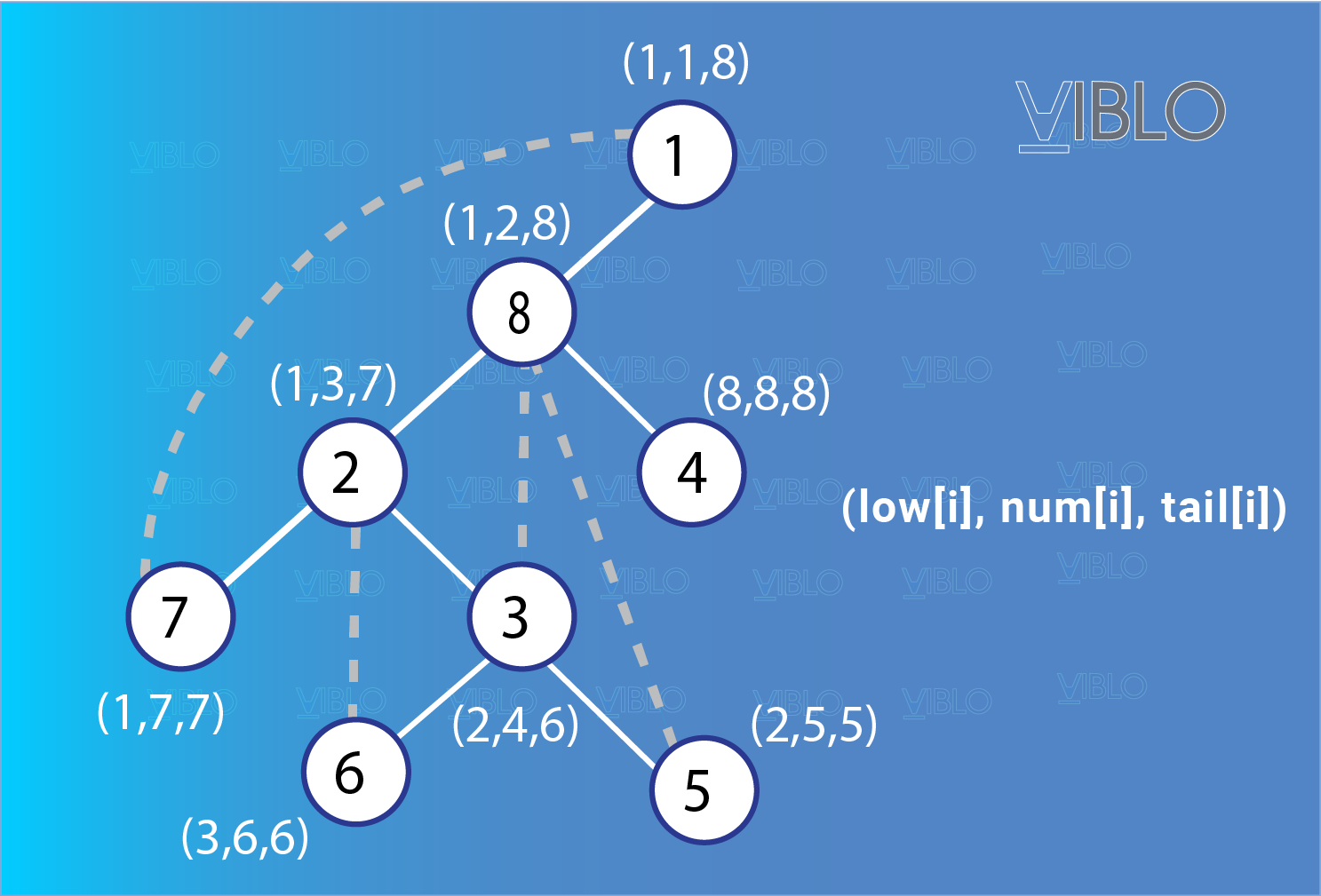
Quá trình $\text{DFS}$ định chiều và đánh số đồ thị diễn ra như sau:

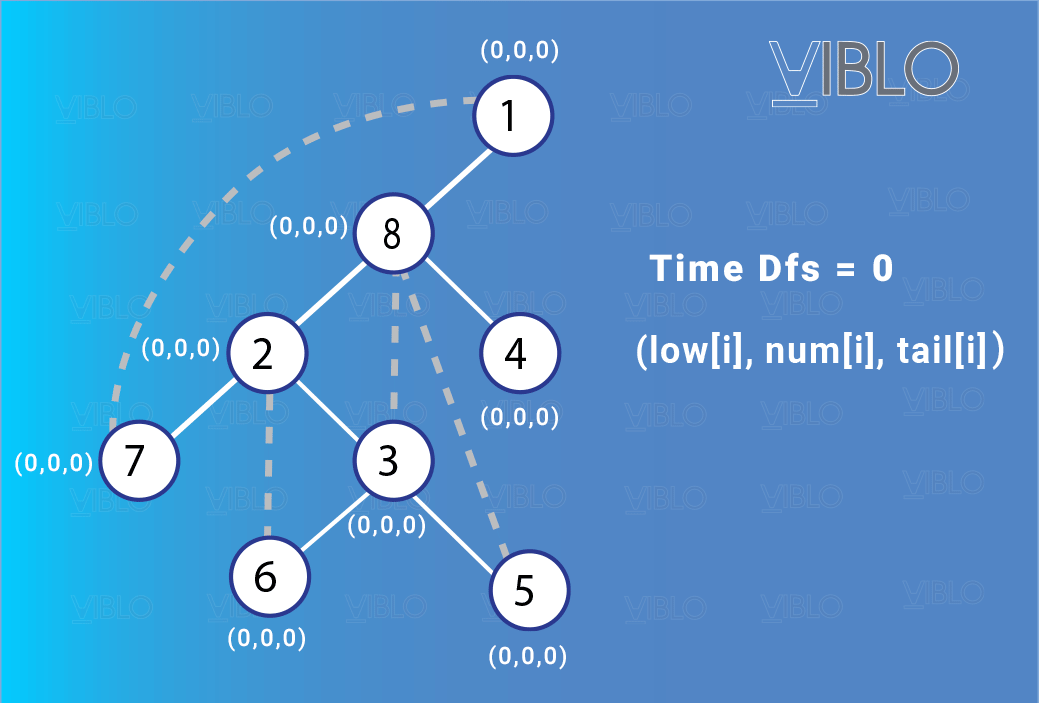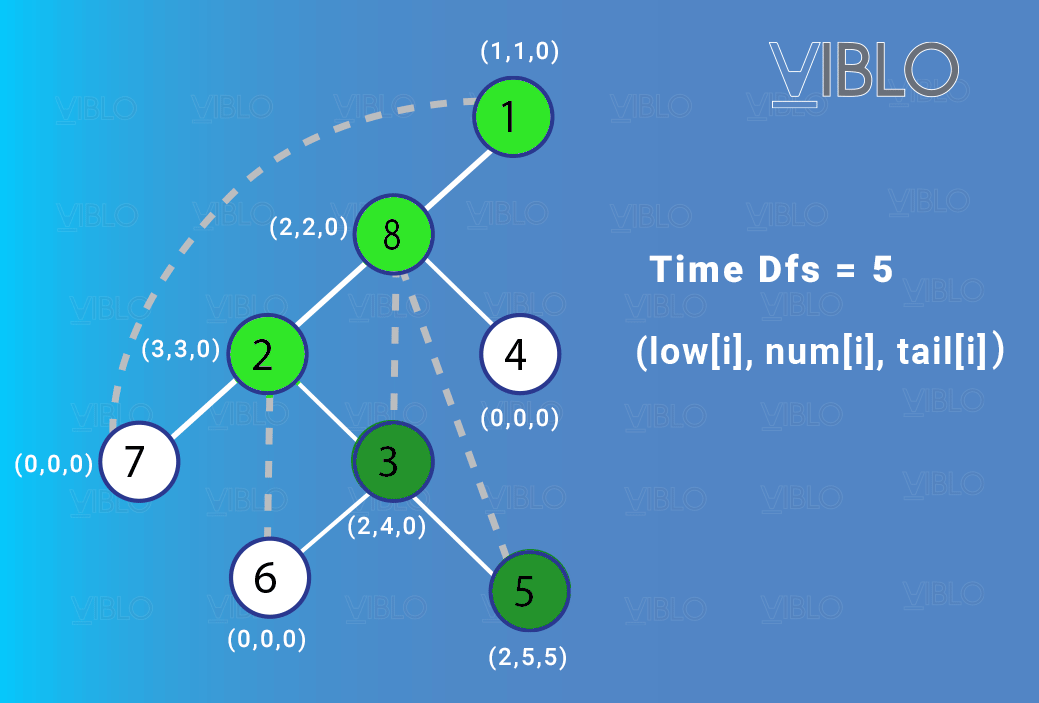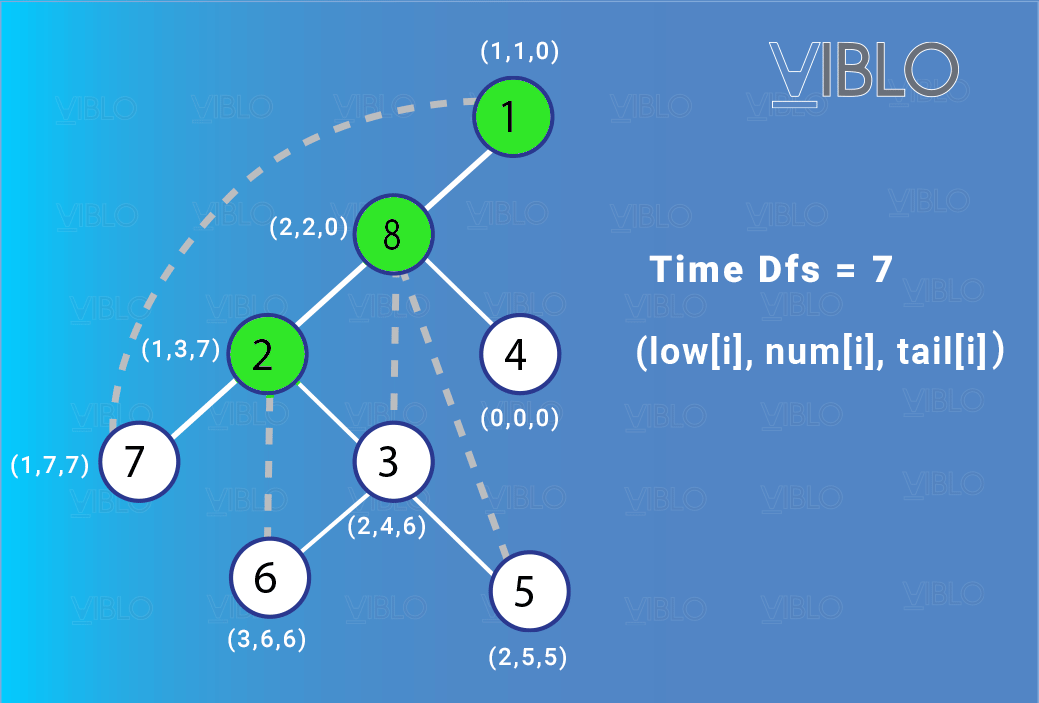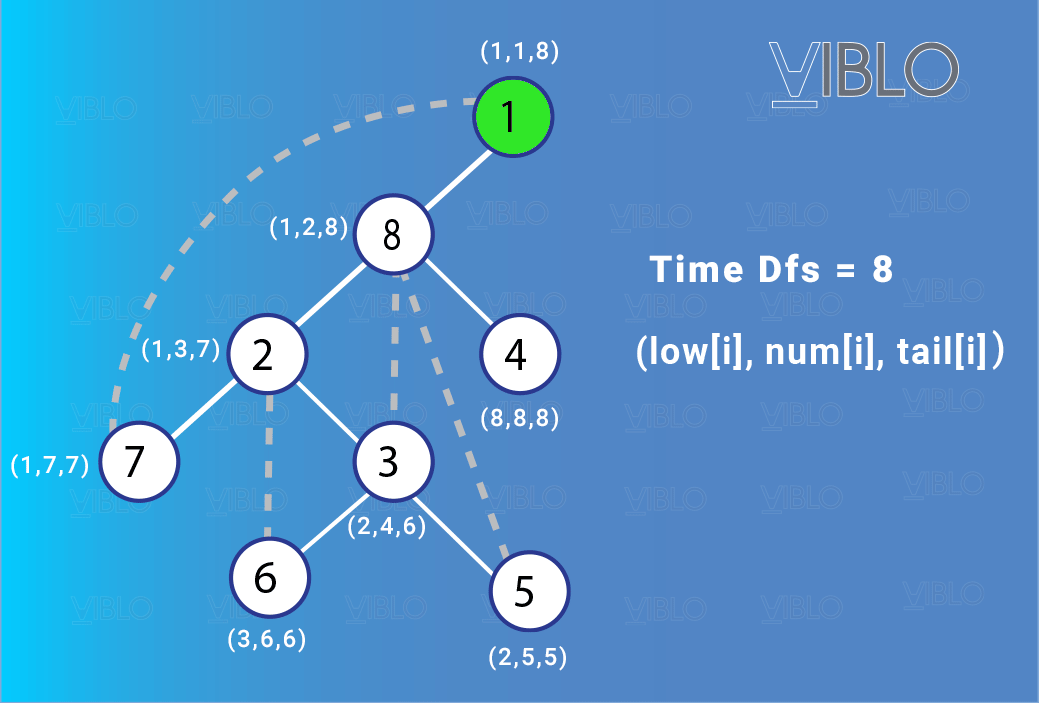
II. Bài toán tìm khớp và cầu của đồ thị

1. Giải thuật tìm khớp và cầu của đồ thị

Bài toán: Cho một đơn đồ thị vô hướng gồm $n$ đỉnh $(1 \le n \le 10^4)$ và $m$ cạnh $(1\le m \le 5 \times 10^4)$. Hãy xác định số lượng đỉnh khớp và cạnh cầu của đồ thị?

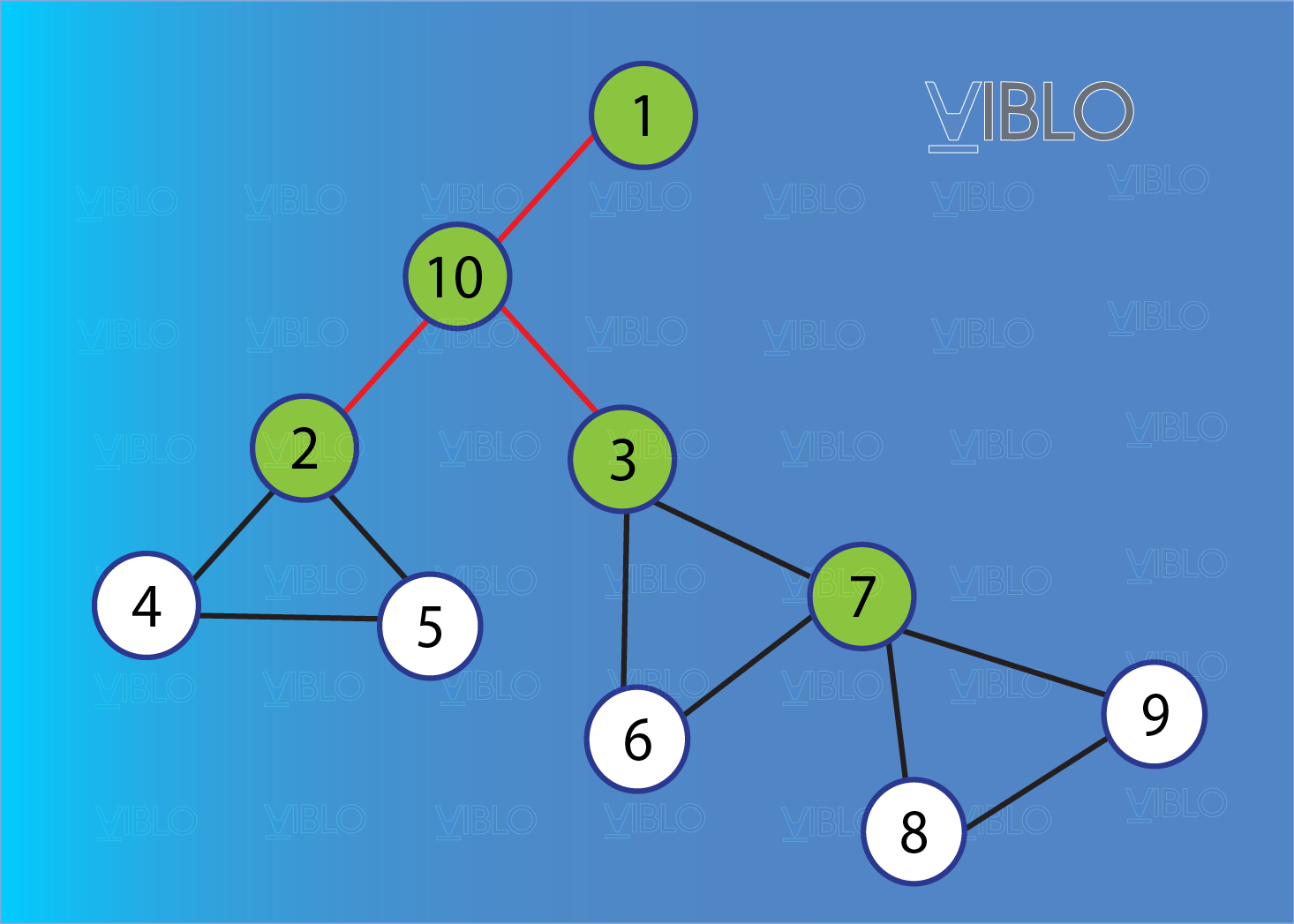
Định nghĩa:

• Một đỉnh được gọi là đỉnh khớp nếu như khi loại bỏ đỉnh này và các cạnh liên thuộc với nó khỏi đồ thị thì số thành phần liên thông của đồ thị tăng lên (các đỉnh màu xanh lá cây).
• Một cạnh được gọi là cạnh cầu nếu như khi loại bỏ cạnh này khỏi đồ thị thì số thành phần liên thông của đồ thị tăng lên (các cạnh màu đỏ).

Nhận xét: Cạnh cầu của đồ thị không thể là cung ngược, do khi bỏ đi cung ngược này thì không ảnh hưởng gì tới tính liên thông của đồ thị. Do đó, cạnh cầu bắt buộc phải là cung thuộc cây $\text{DFS}$.

Hướng giải quyết: Tiến hành dựng cây $\text{DFS}$ và định chiều lại đồ thị đã cho, đồng thời ghi nhận cung ngược lên cao nhất theo giải thuật ở phần $(1.2)$. Xét cung $(u \rightarrow v)$ là cung thuộc cây $\text{DFS},$ ta có:

• Nếu từ nhánh $\text{DFS}$ gốc $v$ không có cung ngược nào lên phía trên $v,$ tức là từ $v$ chỉ có thể đi tới được các cạnh nội bộ của nhánh $\text{DFS}$ gốc $v$ thôi. Lúc này, nếu ta loại bỏ cạnh $(u,v)$ thì nhánh $\text{DFS}$ gốc $v$ sẽ bị chia cắt với các nhánh $\text{DFS}$ khác, do đó số thành phần liên thông của đồ thị sẽ tăng lên. Tức là cạnh $(u,v)$ là cầu khi và chỉ khi $\text{low}_v=\text{num}_v$.
• Nếu từ nhánh $\text{DFS}$ gốc $v$ không có cung nào ngược lên phía trên $u,$ tức là nhánh $\text{DFS}$ gốc $v$ kết nối với các đỉnh khác duy nhất thông qua cạnh $(u, v)$. Khi đó, nếu bỏ đỉnh $u$ đi thì nhánh $DFS$ gốc $v$ cũng sẽ bị chia cắt với các nhánh khác, do đó đỉnh $u$ là đỉnh khớp khi và chỉ khi $\text{low}_v \ge \text{num}_u$.
• Ngoài ra, nếu một đỉnh $u$ là gốc của một cây $\text{DFS}$ và cây này có ít nhất $2$ nhánh con, thì khi bỏ đỉnh $u$ đi, hai nhánh con sẽ bị chia cắt thành $2$ thành phần liên thông khác nhau. Khi đó u cũng là khớp. Để kiểm soát việc này, ta sử dụng thêm một mảng $(cnt_\text{child})_\text{u}$ là số nhánh con của đỉnh $u$. Mảng $is_\text{articulation}[u]$ sẽ dùng để đánh đấu đỉnh $u$ có phải một khớp hay không, nếu có thì $is_\text{articulation}[u] = 1,$ ngược lại $is_\text{articulation}[u] = 0$.

Cài đặt:

#include <bits/stdc++.h>
#define task "GRAPH."
#define inf 1e9 + 7
#define x first
#define y second using namespace std;
const int maxn = 1e5 + 10; // Hai biến cnt_bridge, cnt_articulation dùng để đếm số cầu và khớp.
int n, m, time_dfs, cnt_bridge,cnt_articulation, low[maxn], number[maxn];
int is_articulation[maxn], cnt_child[maxn], par[maxn];
vector < int > adj[maxn]; void enter()
{ cin >> n >> m; for (int i = 1; i <= M; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); adj[v].push_back(u); }
} void dfs(int u)
{ low[u] = number[u] = ++time_dfs; for (int v: adj[u]) { if (v == par[u]) continue; // Đỉnh v chưa thăm thì thăm nó và gắn cha của nó bằng u. if (!number[v]) { par[v] = u; ++cnt_child[u]; dfs(v); low[u] = min(low[u], low[v]); // Cực tiểu hóa low[u]. if (low[v] == number[v]) // cung (u, v) là cầu. ++cnt_bridge; // u là chốt và u có nhiều hơn 1 nhánh con => u là khớp. if (par[u] == -1) { if (cnt_child[u] >= 2) is_articulation[u] = 1; } // u là khớp nếu không có cung ngược hoặc cung chéo đi ra từ nhánh DFS gốc u. else if (low[v] >= number[u]) { is_articulation[u] = 1; } } else { // Cực tiểu hóa low[u] theo number[v] nếu v đã thăm. low[u] = min(low[u], number[v]); } }
} void solution()
{ fill(par + 1, par + 1 + n, -1); for (int u = 1; u <= n; ++u) if (!number[u]) dfs(u); for (int u = 1; u <= n; ++u) cnt_articulation += is_articulation[u]; cout << cnt_articulation << ' ' << cnt_bridge;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); enter(); solution(); return 0;
}

2. Bài toán ví dụ

2.1. Bài toán 1

Nguồn bài: https://bit.ly/3Ft6bWe.

Tóm tắt đề bài: Cho đơn đồ thị vô hướng liên thông $G$ gồm $n$ đỉnh, $m$ cạnh $(1 \le n \le 1000, 1 \le m \le 10000)$. Cần định chiều lại các cạnh của đồ thị thành một chiều, sao cho đồ thị mới vẫn liên thông và số lượng cạnh hai chiều còn lại là ít nhất có thể?

Ý tưởng:

• Áp dụng giải thuật $\text{DFS}$ kết hợp với phép định chiều đồ thị, khi xét tới cạnh $(u, v)$ thì bỏ luôn chiều $(v \rightarrow u)$ và định chiều nó thành cung $(u \rightarrow v)$.
• Tuy nhiên, đối với các cạnh là cầu của đồ thị, việc định chiều lại nó sẽ làm mất tính liên thông của đồ thị. Do đó, nếu sau khi duyệt xong nhánh $\text{DFS}$ gốc $v$ mà thấy cạnh $(u, v)$ là một cầu thì ta sẽ khôi phục lại chiều $(v \rightarrow u)$ cho nó để giữ lại cạnh hai chiều.

Cài đặt:

#include <bits/stdc++.h>
#define int long long
#define task "StreetDirection."
#define inf 1e9 + 7
#define x first
#define y second using namespace std;
const int maxn = 1001;
int n, m, time_dfs, testcase, low[maxn], num[maxn];
bool adj[maxn][maxn]; void reset_data(int n)
{ memset(adj, false, sizeof(adj)); fill(low + 1, low + 1 + n, 0); fill(num + 1, num + 1 + n, 0); time_dfs = 0;
} void enter()
{ cin >> n >> m; reset_data(n); for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; adj[u][v] = true; adj[v][u] = true; }
} void dfs(int u, int par)
{ low[u] = num[u] = ++time_dfs; for (int v = 1; v <= N; ++v) { if (v == par || !adj[u][v]) continue; adj[v][u] = false; // Bỏ luôn chiều (v -> u), định chiều cạnh (u - v) thành cung (u -> v). if (!num[v]) { dfs(v, u); low[u] = min(low[u], low[v]); // Cạnh (u, v) là cầu thì phải giữ nguyên 2 chiều để đảm bảm tính liên thông. if (low[v] == num[v]) adj[v][u] = true; } else { low[u] = min(low[u], num[v]); } }
} void solution()
{ for (int u = 1; u <= n; ++u) if (!num[u]) dfs(u, -1); cout << ++testcase << endl << endl; // In ra các cạnh được định chiều lại thành u -> v. for (int u = 1; u <= n; ++u) for (int v = 1; v <= n; ++v) if (adj[u][v]) cout << u << ' ' << v << endl; cout << "#\n";
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); while (true) { enter(); if (n == 0 && m == 0) break; solution(); } return 0;
}

2.2. Bài toán 2

Nguồn bài: https://bit.ly/3AAbtvj.

Tóm tắt đề bài: Cho một đa đồ thị vô hướng $G$ gồm $n$ đỉnh, $m$ cạnh $(1 \le n \le 100, 1 \le m \le 5000)$. Độ kết dính giữa một cặp đỉnh $(u, v)$ bất kỳ là số lượng cạnh mà nếu bỏ đi sẽ khiến cho hai đỉnh này không còn liên thông nữa. Hãy tính tổng độ kết dính của mọi cặp đỉnh?

Ý tưởng:

• Với mọi cặp đỉnh $(u, v)$ của đồ thị, ta cần quan tâm tới số cạnh cầu trên đường đi từ $u$ tới $v$. Những cạnh này khi bỏ đi sẽ làm $u$ và $v$ mất tính liên thông.
• Đặt $n_\text{children}[u]$ là số đỉnh thuộc nhánh $\text{DFS}$ gốc $u$. Ta xây dựng trong quá trình dựng cây DFS bằng công thức QHĐ đơn giản: $n_\text{children}[u] = \sum n_\text{children}[v],$ với $v$ là con của $u$ và nhánh $\text{DFS}$ gốc $u$ đã duyệt xong.
• Đề bài yêu cầu in ra tổng độ kết dính, tức là tổng số cạnh cầu trên đường đi của mọi cặp đỉnh $(u, v)$. Như vậy ta có thể thay đổi cách tính: Với mỗi cạnh cầu $(u, v)$ của đồ thị, số cặp đỉnh phải đi qua cầu này sẽ là:

$$f(u, v) = n_\text{children}[v] * (n - n_\text{children}[v])$$

(Các đỉnh trong nhánh $\text{DFS}$ gốc $v$ đi tới các đỉnh không thuộc nhánh $\text{DFS}$ gốc $v$)

• Tổng tất cả các giá trị $f(u, v)$ với mọi cạnh cầu sẽ là kết quả bài toán.

Cài đặt:

#include <bits/stdc++.h>
#define int long long
#define task "Weather."
#define inf 1e9 + 7
#define x first
#define y second using namespace std;
const int maxn = 101;
int res, time_dfs, low[maxn], num[maxn], n_children[maxn];
vector < int > adj[maxN]; void enter()
{ cin >> n >> m; for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); adj[v].push_back(u); }
} void dfs(int u, int par)
{ num[u] = low[u] = ++time_dfs; // Tăng số thứ tự duyệt của đỉnh u. n_children[u] = 1; // Ban đầu nhánh DFS gốc u chỉ có chính nó. for (int v: adj[u]) { if (v == par) continue; if (!num[v]) { dfs(v, u); low[u] = min(low[u], low[v]); // Đếm số con nhánh cây DFS gốc u sau khi đã duyệt xong nhánh DFS gốc u. n_children[u] += n_children[v]; // Nếu cung (u, v) là một cạnh cầu. if (low[v] == number[v]) res += n_children[v] * (n - n_children[v]); } else { low[u] = min(low[u], num[v]); } }
} void solution()
{ // Duyệt qua các đỉnh của đồ thị, đỉnh nào chưa thăm thì dựng cây DFS từ đỉnh đó. for (int u = 1; u <= n; ++u) if (!number[u]) dfs(u, -1); cout << res;
} main()
{ enter(); solution(); return 0;
}