III. Bài toán tìm thành phần liên thông mạnh - giải thuật Tarjan

1. Định nghĩa thành phần liên thông mạnh

Đối với đồ thị $G=(V, E)$ có hướng, ta có ba định nghĩa về tính liên thông:

• $G$ được gọi là liên thông mạnh (strongly connected) nếu với mọi cặp đỉnh phân biệt $(u, v)$, ta có $u$ đến được $v$ và $v$ đến được $u$.
• $G$ được gọi là liên thông yếu (weakly connected) nếu như đồ thị vô hướng nền của nó là liên thông (tức là hủy bỏ chiều của các cạnh trên đồ thị).
• $G$ được gọi là liên thông một phần (unilaterally connected) nếu như với mọi cặp đỉnh phân biệt $(u, v),$ có ít nhất một đỉnh đến được đỉnh còn lại.

Như vậy, có thể hiểu một thành phần liên thông mạnh của một đồ thị có hướng là một đồ thị con tối đại liên thông mạnh (nghĩa là nếu thêm vào thành phần liên thông này một tập hợp đỉnh khác sẽ làm mất đi tính liên thông mạnh). Nếu mỗi thành phần liên thông mạnh được co lại thành một đỉnh, thì đồ thị sẽ trở thành một đồ thị có hướng không chu trình. Giải thuật Tarjan là một giải thuật rất được ưa thích để tìm các thành phần liên thông mạnh trên đồ thị.

2. Các định lý quan trọng

Có ba định lý rất quan trọng sử dụng trong quá trình phát triển giải thuật Tarjan:

Định lý 1

Nếu $a$ và $b$ là hai đỉnh thuộc thành phần liên thông mạnh $C$ thì mọi đường đi từ $a$ tới $b$ cũng giống như đường đi từ $b$ tới $a$. Tất cả các đỉnh trung gian trên đường đi đó đều phải thuộc $C$.

Chứng minh: Nếu $a$ và $b$ là hai đỉnh thuộc $C$ thì tức là có một đường đi từ $a$ đến $b$ và một đường khác đi từ $b$ về $a$. Suy ra với một đỉnh $v$ nằm trên đường đi từ $a$ tới $b$ thì $a$ tới được $v, v$ tới được $b,$ mà $b$ có đường tới $a$ nên $v$ cũng tới được $a$. Vậy $v$ nằm trong thành phần liên thông mạnh chứa $a$ tức là $v$ thuộc $C$. Tương tự với một đỉnh nằm trên đường đi từ $b$ tới $a$.

Định lý 2

Với một thành phần liên thông mạnh $C$ bất kỳ, sẽ tồn tại một đỉnh $r∈C$ sao cho mọi đỉnh của $C$ đều thuộc nhánh $\text{DFS}$ gốc $r$. Đặt đỉnh $r$ này là đỉnh thăm đầu tiên trong quá trình dfs trên thành phần $C,$ ta có $r$ là chốt của $C$.

Chứng minh: Trước hết, nhắc lại một thành phần liên thông mạnh là một đồ thị con liên thông mạnh của đồ thị ban đầu thoả mãn tính chất tối đại tức là việc thêm vào thành phần đó một tập hợp đỉnh khác sẽ làm mắt đi tính liên thông mạnh. Trong số các đỉnh của $C,$ chọn $r$ là đỉnh được thăm đầu tiên theo thuật toán tìm kiếm theo chiều sâu. Ta sẽ chứng minh $C$ nằm trong nhánh $\text{DFS}$ gốc $r$. Thật vậy, với một đỉnh $v$ bất kỳ của $C,$ do $C$ liên thông mạnh nên phải tồn tại một đường đi từ $r$ tới $v$: $r=x_0,x_1,…,x_k=v$

Từ định lý $1,$ tất cả các đỉnh $x_1,x_2,…,x_k$ đều thuộc $C$ nên chúng sẽ phải thăm sau đỉnh $r$. Khi hàm $\text{DFS}(r)$ được gọi thì tất cả các đỉnh $x_1,x_2,…,x_k$ đều chưa thăm; vì hàm $\text{DFS}(r)$ sẽ liệt kê tất cả những đỉnh chưa thăm đến được từ $r$ bằng cách xây dựng nhánh gốc $r$ của cây $DFS,$ nên các đỉnh $x_1,x_2,…,x_k=v$ sẽ thuộc nhánh gốc $r$ của cây $\text{DFS}$. Bởi chọn $v$ là đỉnh bất kỳ trong $C$ nên ta có điều phải chứng minh. Đỉnh $r$ trong chứng minh định lý - đỉnh thăm trước tất cả các đỉnh khác trong $C$ - gọi là chốt của thành phần $C$. Mỗi thành phần liên thông mạnh có duy nhất một chốt. Xét về vị trí trong cây tìm kiếm DFS, chốt của một thành phân liên thông là đỉnh nằm cao nhất so với các đỉnh khác thuộc thành phần đó, hay nói cách khác: là tiền bối của tất cả các đỉnh thuộc thành phần đó.

Định lý 3

Luôn tìm được đỉnh chốt $a$ thỏa mãn: Quá trình tìm kiếm theo chiều sâu bắt đầu từ $a$ không thăm được bất kỳ một chốt nào khác (tức là nhánh $\text{DFS}$ gốc $a$ không chứa một chốt nào ngoài $a$). Chẳng hạn, ta chọn a là chốt được thăm sau cùng trong một dây chuyền đệ quy hoặc chọn $a$ là chốt thăm sau tất cả các chốt khác. Với chốt $a$ như vậy thì các đỉnh thuộc nhánh $\text{DFS}$ gốc $a$ chính là thành phần liên thông mạnh chứa $a$.

Chứng minh: Với mọi đỉnh $v$ nằm trong nhánh $\text{DFS}$ gốc $a,$ xét $b$ là chốt của thành phần liên thông mạnh chứa $v$. Ta sẽ chứng minh $a=b$. Thật vậy, theo định lý $2, v$ phải nằm trong nhánh $\text{DFS}$ gốc $b$. Vậy $v$ nằm trong cả nhánh $\text{DFS}$ gốc $a$ và nhánh $\text{DFS}$ gốc $b$. Giả sử phản chứng rằng $a$ khác $b$ thì sẽ có hai trường hợp xảy ra:

• Trường hợp $1$: Nhánh $\text{DFS}$ gốc $a$ chứa nhánh $\text{DFS}$ gốc $b,$ có nghĩa là hàm $\text{DFS}(b)$ sẽ do hàm $\text{DFS}(a)$ gọi tới, điều này mâu thuẫn với giả thiết rằng $a$ là chốt mà quá trình tìm kiếm theo chiều sâu bắt đầu từ $a$ không thăm một chốt nào khác.
• Trường hợp $2$: Nhánh $\text{DFS}$ gốc $a$ nằm trong nhánh $\text{DFS}$ gốc $b,$ có nghĩa là $a$ nằm trên một đường đi từ $b$ tới $v$. Do $b$ và $v$ thuộc cùng một thành phần liên thông mạnh nên theo định lý $1, a$ cũng phải thuộc thành phần liên thông mạnh đó. Vậy thì thành phần liên thông mạnh này có hai chốt $a$ và $b$. Điều này vô lý.

Theo định lý $2,$ ta đã có thành phân liên thông mạnh chứa $a$ nằm trong nhánh $\text{DFS}$ gốc $a,$ theo chứng minh trên ta lại có: Mọi đỉnh trong nhánh $\text{DFS}$ gốc $a$ nằm trong thành phân liên thông mạnh chứa $a$. Kết hợp lại được: Nhánh $\text{DFS}$ gốc $a$ chính là thành phần liên thông mạnh chứa a.

3. Giải thuật Tarjan

3.1. Ý tưởng

Giải thuật Tarjan có thể phát biểu như sau: Chọn $r$ là chốt không là tiền bối của một chốt nào khác, chọn lấy thành phần liên thông mạnh thứ nhất là nhánh $\text{DFS}$ gốc $r$. Sau đó loại bỏ nhánh DFS gốc $r$ ra khỏi cây $\text{DFS},$ lại tìm thấy một chốt $s$ khác mà nhánh $\text{DFS}$ gốc $s$ không chứa chốt nào khác, lại chọn lấy thành phần liên thông mạnh thứ hai là nhánh DFS gốc $s,...$ Tương tự như vậy cho thành phần liên thông mạnh thứ ba, thứ tư, v.v… Có thể hình dung thuật toán Tarjan “bẻ” cây $\text{DFS}$ tại vị trí các chốt để thu được các nhánh rời rạc, mỗi nhánh là một thành phần liên thông mạnh.

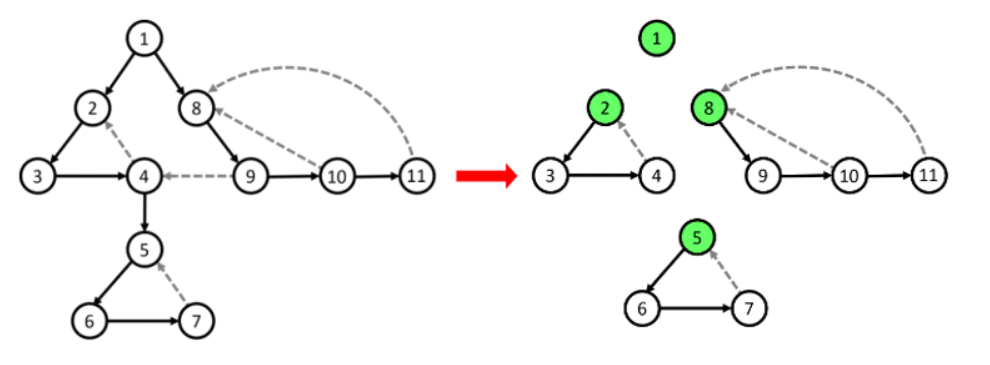
Mô hình thuật toán:

void dfs(u)
{ {Đánh_dấu_đã_thăm_u}; // Duyệt các đỉnh v kề với u. for (v in adj[u]) if {v_chưa_thăm} dfs(v); if {u_là_chốt} { {Liệt_kê_thành_phần_liên_thông_mạnh_chốt_u}; {Loại_bỏ_các_đỉnh_đã_liệt_kê_khỏi_đồ_thị}; }
} main()
{ {Đánh_dấu_mọi_đỉnh_v_đều_chưa_thăm}; // Duyệt mọi đỉnh u thuộc tập đỉnh V của đồ thị G. for (u in V) if (u_chưa_thăm) dfs(u);
}

3.2. Xác định một đỉnh có phải là chốt hay không

Ý tưởng thì khá dễ hiểu, tuy nhiên, làm thế nào để xác định được một đỉnh $r$ có phải là chốt hay không thì lại là câu chuyện khác. Để làm được như thế, ta dựa vào các nhận xét dưới đây:

• Nhận xét 1: Xét một nhánh $\text{DFS}$ gốc $r$. Nếu như trong nhánh này không có cung ngược hoặc cung chéo nào đi ra khỏi nhánh đó thì chắc chắn $r$ là chốt. Điều này dễ dàng chứng minh bởi vì từ $r$ ta chỉ đến được các đỉnh thuộc nhánh đó mà thôi, do đó $r$ là chốt.
• Nhận xét 2: Nếu từ một đỉnh $v$ nào đó của nhánh $\text{DFS}$ gốc $r$ có một cung ngược tới đỉnh $w$ bất kỳ là cha của $r$ thì $r$ không thể là chốt. Bởi vì nếu như vậy, ta sẽ có chu trình: $w→r→v→w,$ nên $w,r,v$ thuộc cùng một thành phần liên thông mạnh. Mà $w$ lại được thăm trước $r,$ trong khi đang giả sử $r$ là chốt (đỉnh được duyệt đầu tiên trong TPLT mạnh) nên điều này mâu thuẫn.
• Nhận xét 3: Trong trường hợp nếu giữa hai nhánh $\text{DFS}$ gốc $r$ và gốc $r’$ tồn tại một cung chéo $(v,v’),$ thì $r$ cũng không thể là chốt. Thật vậy, cung chéo $(v,v’)$ này buộc phải đi từ nhánh thăm sau tới nhánh thăm trước (tính chất cây $\text{DFS}$), tức là nhánh gốc $r’$ phải thăm trước nhánh gốc $r,$ suy ra $v’$ phải thăm trước $r$ và $r’$ cũng phải thăm trước $r$. Lúc này, tồn tại hai khả năng có thể xảy ra:
  • Nếu $r’$ thuộc nhánh $\text{DFS}$ đã duyệt trước $r,$ thì $r’$ sẽ được duyệt xong trước khi thăm tới $r$. Vậy khi quá trình $\text{DFS}$ gọi tới $r$ thì toàn bộ các đỉnh trong nhánh $\text{DFS}$ gốc $r’$ đã được duyệt xong (nói cách khác là đã bị hủy đi), nên sẽ không tiến hành $\text{DFS}$ tiếp từ đỉnh $v$ sang đỉnh $v’$ nữa. Lúc này cung $(v,v’)$ bị hủy.
  • Nếu $r’$ là cha của $r$ thì ta có: $r’$ tới được $r, v$ lại nằm trong nhánh $\text{DFS}$ gốc $r$ nên $r$ đến được $v,$ mà $v$ đến được $v’$ do $(v,v’)$ là một cung, $v’$ lại đến được $r’$ do $v’$ thuộc thành phần liên thông mạnh gốc $r’$. Như vậy ta có chu trình: $r’→r→v→v’→r’,$ suy ra $r$ và $r’$ thuộc cùng một thành phần liên thông mạnh. Mà $r’$ đã duyệt trước $r$ nên $r$ không thể là một chốt nữa.

Tựu chung lại, đỉnh $r$ là một chốt khi và chỉ khi không tồn tại cung ngược hoặc cung chéo nối từ nhánh $\text{DFS}$ gốc $r$ sang một nhánh gốc $r’$ khác. Nói cách khác, $r$ là chốt nếu như không tồn tại cung nối từ nhánh $\text{DFS}$ gốc $r$ tới một đỉnh đã thăm trước $r$.

4. Cài đặt

Dựa vào ý tưởng đánh số các đỉnh trên cây $\text{DFS}$ và ghi nhận cung ngược lên cao nhất, ta có thể kiểm tra được từ một đỉnh $u$ có tồn tại cung nối thuộc nhánh $\text{DFS}$ gốc $u$ tới một đỉnh thăm trước $u$ hay không. Nếu có thì $u$ sẽ không thể là chốt, ngược lại thì $u$ là chốt. Cụ thể như sau:

• Sử dụng mảng $\text{num}[u]$ là số thứ tự duyệt $\text{DFS}$ của đỉnh $u$ và $\text{low}[u]$ là giá trị $\text{num}[]$ nhỏ nhất mà từ nhánh $\text{DFS}$ gốc $u$ có thể tới được bằng một cung (giống với cách xây dựng cây $\text{DFS}$). Ban đầu tăng $\text{num}[u]$ lên và khởi gán $\text{low}[u] = \text{num}[u]$ trong quá trình $\text{DFS}$.
• Sử dụng thêm mảng \text{is_deleted}[u] để đánh dấu đỉnh $u$ đã bị loại khỏi đồ thị hay chưa. $is_\text{deleted}[u] = true$ nếu $u$ đã xóa và ngược lại.
• Dựa vào nhận xét số $3,$ ta có một cách cài đặt tiện lợi sử dụng cấu trúc dữ liệu stack như sau: Khi duyệt xong một nhánh $\text{DFS}$ gốc $u,$ trước khi thoát khỏi hàm $\text{dfs}(u),$ ta kiểm tra $u$ có phải là chốt không bằng cách so sánh $\text{low}[u]$ và $\text{num}[u]$. Nếu $\text{low}[u] = \text{num}[u]$ thì từ $u$ chỉ tới được các đỉnh thuộc nhánh $\text{DFS}$ gốc $u,$ từ đó $u$ là chốt và các đỉnh thuộc nhánh $\text{DFS}$ gốc $u$ chính là các đỉnh thuộc thành phần liên thông mạnh chốt là $u$. Trong quá trình $\text{DFS},$ khi thăm tới một đỉnh $u,$ ta sẽ đẩy ngay nó vào stack. Như vậy khi duyệt xong đỉnh $u$ thì các đỉnh thuộc nhánh $\text{DFS}$ gốc $u$ sẽ nằm liên tiếp ngay cạnh nhau trong stack. Nếu $u$ là chốt, ta chỉ cần lấy ra các đỉnh này tới khi lấy được đỉnh $u,$ toàn bộ các đỉnh đó chính là thành phần liên thông mạnh chứa $u$.

#include <bits/stdc++.h> using namespace std; const int maxn = 1e5 + 10;
int cnt_components, time_dfs, number[maxn], low[maxn];
stack < int > vertex;
bool is_deleted[maxn];
vector < int > adj[maxn]; void dfs(int u) // Giải thuật Tarjan
{ number[u] = ++time_dfs; low[u] = num[u]; for (int v: adj[u]) { if (is_deleted[v]) // Đỉnh v đã xóa rồi thì bỏ qua. continue; if (!number[v]) // đỉnh v chưa được đánh số => chưa được thăm. { dfs(v); // Thăm v. low[u] = min(low[u], low[v]); // Cực tiểu hóa low[u]. } else // Nếu v đã thăm. { low[u] = min(low[u], num[v]); // Cực tiểu hóa low[u] theo num[v]. } } // Bắt đầu kiểm tra đỉnh u có phải chốt hay không. if (low[u] == num[u]) { // In ra chỉ số của thành phần liên thông này. cout << "Strongly Connected Component " << ++cnt_components << ": "; // Liệt kê thành phần liên thông mạnh chốt là u. int v; do { v = vertex.top(); // Lấy các đỉnh từ trong stack ra. cout << v << ‘ ‘; vertex.pop(); is_deleted[v] = 1; } while (v != u); // Nếu đã lấy ra chốt u thì kết thúc TPLTM chốt u. cout << endl; }
} main()
{ // Nhập dữ liệu đồ thị. int n, m; cin >> n >> m; for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); } // Duyệt qua các đỉnh, nếu đỉnh nào chưa thăm thì bắt đầu dfs từ đỉnh đó. for (int u = 1; u <= N; ++u) if (!number[u]) dfs(u);
}

Giả sử với dữ liệu đồ thị $G(V, E)$ như hình dưới đây:

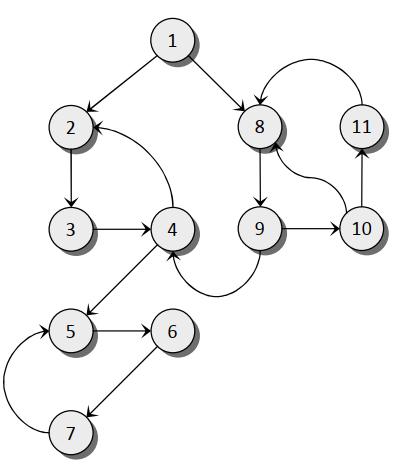
Chạy chương trình trên sẽ cho ra kết quả:

Strongly Connected Component 1: 7 6 5
Strongly Connected Component 2: 4 3 2
Strongly Connected Component 3: 11 10 9 8
Strongly Connected Component 4: 1

Đánh giá độ phức tạp: Bởi vì giải thuật Tarjan chỉ là sửa đổi một chút từ giải thuật $\text{DFS},$ các phép toán vào/ra của ngăn xếp được thực hiện không quá $n$ lần, nên thời gian thực hiện giải thuật vẫn là $O(n + m)$ trong trường hợp đồ thị được biểu diễn bằng danh sách kề, $O(n^2)$ nếu dùng ma trận kề và $O(n \times m)$ nếu dùng danh sách cạnh.

5. Bài toán ví dụ

Nguồn bài: https://bit.ly/3lv0MG9.

Tóm tắt đề bài: Cho đa đồ thị có hướng gồm $n$ đỉnh, $m$ cạnh $(1 \le n \le 10^5, 0 \le m \le 2 \times 10^5)$. Hai đỉnh $a$ và $b$ được gọi là thân thiện nếu như từ $a$ tới được $b$ và từ $b$ cũng tới được $a$. Cần thêm vào đồ thị một số cung sao cho các cặp đỉnh thân thiện đều có đường nối trực tiếp với nhau và số cung thêm vào là ít nhất có thể (cung thêm vào không được trùng với các cung đã có)?

Ý tưởng:

• Nhận xét: Các cặp thành phố thân thiện chỉ có thể là các cặp thành phố nằm trong cùng một TPLT mạnh.
• Từ nhận xét trên, bước $1$ ta tìm các TPLT mạnh của đồ thị, với mỗi TPLT mạnh, số cung tối đa cần thêm là $e = k \times (k - 1)$ cung, với $k$ là số đỉnh thuộc TPLT mạnh đó. Ta sẽ đếm số cung nối trực tiếp đã có sẵn trong TPLT mạnh đó (gọi là $d$), tính toán ra số cạnh tối thiểu cần thêm trong TPLT mạnh này là $(e - d)$.
• Lưu ý đồ thị đã cho là đa đồ thị, mỗi cặp đỉnh có thể có nhiều cạnh nối trực tiếp, do đó cần lưu ý khi xử lý để không trừ cạnh giữa $2$ cặp đỉnh nhiều lần. Ví dụ có $2$ cạnh nối từ đỉnh $1$ tới đỉnh $2$ thì cũng chỉ tính là $1$ cung trực tiếp đã có và chỉ trừ đi $1$ lần thôi.

Cài đặt:

#include <bits/stdc++.h>
#define int long long
#define task "NewRoads."
#define inf 1e9 + 7
#define x first
#define y second using namespace std; const int maxn = 1e5 + 10;
int n, m, time_dfs, minimum_new_roads, cnt_comps;
int par[maxn], component_num[maxn], num[maxn], low[maxn];
bool is_deleted[maxn];
stack < int > vertex;
vector < int > adj[maxn], component[maxn]; void enter()
{ cin >> N >> M; for (int i = 1; i <= M; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); }
} // Đếm số cạnh cần thêm trong 1 TPLT mạnh có K đỉnh.
int cntNewRoads(vector < int > component) { // par[v] = u: Tồn tại một cung (u -> v). Mảng này để kiểm soát các cung nối cùng 1  // cặp đỉnh, tránh trừ nhiều lần. int k = component.size(), had_directed_edges = 0; for (int u: component) { for (int v: adj[u]) if (par[v] != u && componentNum[v] == componentNum[u]) { par[v] = u; ++had_directed_edges; } } return k * (k - 1) - had_directed_edges;
} // Xác định các TPLT mạnh bằng giải thuật Tarjan.
void tarjan(int u) { num[u] = low[u] = ++time_dfs; vertex.push(u); for (int v: adj[u]) { if (is_deleted[v]) continue; if (num[v]) { low[u] = min(low[u], num[v]); } else { tarjan(v); low[u] = min(low[u], low[v]); } } if (low[u] == num[u]) { vector < int > component_vertexes; int v; ++cnt_comps; do { v = vertex.top(); vertex.pop(); is_deleted[v] = true; // Nạp đỉnh v vào danh sách các đỉnh trong tplt thứ cnt. component_vertexes.push_back(v); // Đánh số hiệu cho v: Nằm trong thành phần liên thông thứ cnt. component_num[v] = cnt_comps; } while (v != u); minimum_new_roads += cnt_new_roads(component_vertexes); }
} void solution()
{ for (int u = 1; u <= N; ++u) if (!num[u]) tarjan(u); cout << minimum_new_roads;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); enter(); solution(); return 0;
}

IV. Tài liệu tham khảo

• https://vnoi.info/wiki/algo/graph-theory/Depth-First-Search-Tree.md#thuật-toán-tarjan.
• Sách Giải thuật và Lập trình - thầy Lê Minh Hoàng.