Giới thiệu

Toán học là làm việc với những con số và các phép tính. Khi làm việc với những con số và các phép tính như vậy, ta có thể phát hiện ra những con số, phương trình hay ma trận có những tính chất rất đẹp và Ma phương là một trong số đó. Hãy thử tìm hiểu tất cả những điều hay ho của ma phương nhé.

Một ma phương là một ma trận vuông sao cho tổng các số trong mỗi hàng, mỗi cột và 2 đường chéo chính bằng nhau. Bậc của ma phương là số lượng các số nguyên dọc theo một cạnh ($n$). Nếu ma phương gồm các số nguyên từ $1$ đến $n^2$, ma phương đó được gọi là bình thường. Để đơn giản hóa bài toán, trong bài viết mình sẽ đề cập đến việc xây dựng ma phương này.

Tính chất của ma phương

Ma phương tầm thường: Ma phương $1 × 1$, chỉ có một ô chứa số $1$, được gọi là tầm thường, vì nó thường không được xem xét khi thảo luận về ma phương. Nhưng nó thực sự là một ma phương theo định nghĩa, nếu chúng ta coi một ô đơn lẻ là một hình vuông có bậc một.

Hằng số ma thuật: Mọi ma phương bình thường có hằng số phụ thuộc vào bậc $n$, được tính bằng công thức ${ M = n ( n ^ {2} +1) / 2}$. Điều này có thể được chứng minh bằng cách lưu ý rằng tổng của ${ 1,2, ..., n ^ {2}}$ là ${ n ^ {2} (n ^ {2} +1) / 2}$. Vì tổng của mỗi hàng là ${ M}$ nên tổng của ${ n}$ hàng là ${ nM = n ^ {2} (n ^ {2} +1) / 2}$, khi chia cho bậc $n$ sẽ thu được hằng số ma thuật. Đối với các ma phương thông thường có bậc $n = 3, 4, 5, 6, 7$ và $8$, các hằng số ma thuật lần lượt là: $15, 34, 65, 111, 175$ và $260$

Không thể xây dựng ma phương bậc 2: Ma phương bình thường ở mọi kích thước có thể được tạo ngoại trừ $2 × 2$ (nghĩa là, trong đó bậc của ma phương là $n = 2$)

Tâm khối lượng: Nếu ta coi các số trong ma phương là khối lượng nằm trong các ô khác nhau, thì tâm khối của ma phương trùng với tâm hình học của nó.

Moment quán tính: Moment quán tính của ma phương được định nghĩa là tổng tất cả các số trong ô nhân với bình phương khoảng cách từ tâm ô đến tâm hình vuông. Ở đây đơn vị đo lường là chiều rộng của một ô. (Ví dụ: ô góc của hình vuông $3 × 3$ có khoảng cách là ${\sqrt {2}}$, ô ở bên cạnh không phải góc có khoảng cách là $1$, và ô chính giữa có khoảng cách bằng $0$). Khi đó tất cả các ma phương của một bậc đã cho đều có cùng moment quán tính với nhau. Đối với trường hợp bậc $3$, moment quán tính luôn là $60$, trong khi đối với trường hợp $4$, moment quán tính luôn là $340$. Nói chung, đối với trường hợp $n × n$, moment quán tính là ${n ^ {2 } (n ^ {4} -1) / 12}$.

Phép phân tích Birkhoff – von Neumann: Chia từng số của ô trong ma phương cho hằng số ma thuật sẽ tạo ra ma trận ngẫu nhiên kép, có tổng hàng và tổng cột bằng $1$. Tuy nhiên, không giống như ma trận ngẫu nhiên kép, tổng đường chéo của các ma trận như vậy cũng sẽ bằng $1$. Do đó, các ma trận như vậy tạo thành một tập hợp con của ma trận ngẫu nhiên kép. Định lý Birkhoff – von Neumann phát biểu rằng đối với bất kỳ ma trận ngẫu nhiên kép nào ${A}$, tồn tại các số thực ${\theta_{1}, \ldots, \theta_{k} \geq 0}$, trong đó ${\sum_{i = 1} ^ {k} \theta_{i} = 1}$ và ma trận hoán vị ${P_{1}, \ldots, P_{k}}$ sao cho ${A = \theta_{1} P_{1} + \cdots + \theta_{k} P_{k}}$. Nói chung, cách biểu diễn này có thể không phải là duy nhất. Tuy nhiên, theo định lý Marcus-Ree, không cần nhiều hơn ${k \leq n ^ {2} -2n + 2}$ trong bất kỳ phép phân tích nào. Rõ ràng, sự phân rã này cũng chuyển sang hình vuông ma thuật, vì chúng ta có thể khôi phục một hình vuông ma thuật từ ma trận ngẫu nhiên kép bằng cách nhân nó với hằng số ma thuật.

Xây dựng ma phương

Đề bài: Nếu có kỹ năng quan sát tốt, bạn có thể thấy rằng việc xây dựng ma phương rất đơn giản. Một ma phương chỉ có một số lẻ $N$ hàng và cột. Đối với bài toán này, giá trị $N$ sẽ nằm trong đoạn $3 ≤ N ≤ 15$. Một Ma phương được tạo bởi các số nguyên trong phạm vi từ 1 đến $N^2$, với một thuộc tính đặc biệt, "tổng các số" trong mỗi hàng, cột và đường chéo có cùng giá trị.

INPUT Đầu vào gồm một số dòng, mỗi dòng gồm một giá trị $N$.

OUTPUT

Đối với mỗi dòng, in ra $N$ và tổng ở dòng đầu tiên, tiếp theo là chi tiết giá trị mỗi ô trong ma phương (Bạn có thể tham khảo chi tiết trong Output mẫu)

Input mẫu

3
5

Output mẫu

n=3, sum=15
8 1 6
3 5 7
4 9 2 n=5, sum=65
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9

Hướng giải quyết

Nếu không biết lời giải, ta có thể phải sử dụng quy trình quay lui đệ quy tiêu chuẩn cố gắng đặt từng số nguyên $∈ [1..n^2]$ vào tưng ô một. Với $n$ lớn thì cách làm này thật sự không hiệu quả.

May mắn thay, có một cách xây dựng rất đẹp cho ma phương với bậc là số lẻ được gọi là 'phương pháp Siam. Ta bắt đầu từ một mảng vuông 2D trống. Ban đầu, ta đặt số nguyên 1 ở giữa hàng đầu tiên. Sau đó, ta di chuyển về phía đông bắc (hướng phải trên ). Nếu ô mới hiện đang trống, ta thêm số nguyên tiếp theo vào ô đó. Nếu ô đã đã được điền, ta di chuyển xuống một hàng và tiếp tục đi về phía đông bắc. Phương pháp Siam này được thể hiện trong hình dưới. Việc tìm ra được cách giải này khá khoai nếu như bạn mới bắt đầu tìm hiểu về ma phương .

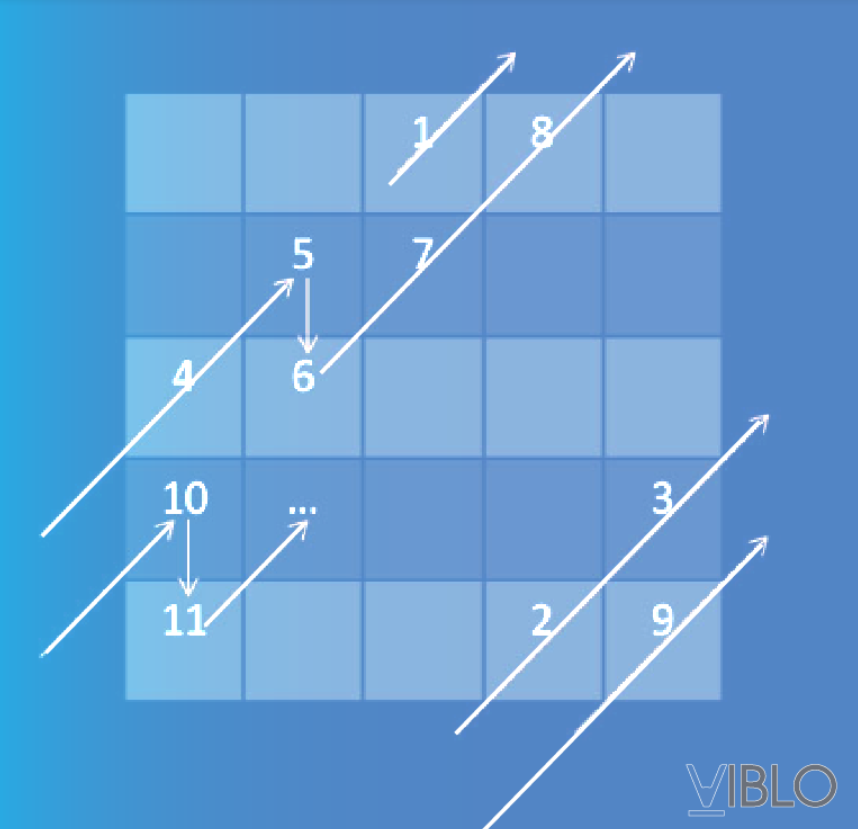
Solution mẫu

#include<stdio.h>
#include<string.h>
int main() { int n, i, j, first = 0; while(scanf("%d", &n) == 1) { if(first) puts(""); first = 1; printf("n=%d, sum=%d\n", n, n*(n*n+1)/2); int map[15][15], x = 0, y = n/2; memset(map, 0, sizeof(map)); for(i = 1; i <= n*n; i++) { if(map[x][y]) { x += 2, y--; if(x >= n)	x -= n; if(y < 0) y += n; map[x][y] = i; } else map[x][y] = i; x--, y++; if(x < 0)	x += n; if(y >= n)	y -= n; } if(n*n <= 9) { for(i = 0; i < n; i++, puts("")) for(j = 0; j < n; j++) printf("%2d", map[i][j]); } else if(n*n >= 10 && n*n <= 100) { for(i = 0; i < n; i++, puts("")) for(j = 0; j < n; j++) printf("%3d", map[i][j]); } else { for(i = 0; i < n; i++, puts("")) for(j = 0; j < n; j++) printf("%4d", map[i][j]); } } return 0;
}

Tổng kết

Có những trường hợp đặc biệt khác đối với việc xây dựng ma phương với các kích thước khác nhau. Có thể không cần thiết phải học tất cả chúng vì rất có thể nó sẽ không xuất hiện trong cuộc thi lập trình. Tuy nhiên, biết các chiến lược về xây dựng ma phương sẽ là một lợi thề trong kì thi nếu bài toán này xuất hiện

Tài liệu tham khảo

1. Giải thuật và lập trình - Thầy Lê Minh Hoàng
2. cp-algorithms.com
3. Handbook Competitive Programming - Antti Laaksonen
4. Competitve programming 3 - Steven Halim, Felix Halim
5. onlinejudge.org
6. https://en.wikipedia.org/wiki/Magic_square