Index leaf node được lưu trữ theo dạng Linked List về mặt logic, còn về cấu trúc lưu trữ vật lý, mỗi leaf node có thể lưu lung tung, không có thứ tự gì, nó giống một quyền từ điển mà các trang bị xáo trộn, khi ta cần tra từ "Phở" mà đang lật tới trang có từ "Cơm" không có nghĩa là từ Phở chắc chắn ở sau từ Cơm. Để đáp ứng việc tìm kiếm nhanh trong các trang xáo trộn này , database cung cấp một kiểu dữ liệu khác là Cây Tìm Kiếm Cân Bằng (a balanced search tree) gọi ngắn là B-Tree (chú ý các bạn không nên nhầm với Cây nhị phân Binary tree nhé).

Hình trên mình mô tả một index với 30 cục, Danh sách liên kết đôi mô tả thứ tự logic giữa Leaf Node, còn Root Node và Branch Node hỗ trợ việc tìm kiếm nhanh giữa các Leaf Node. Các bạn nhìn trong hình bên mỗi một cục trên Branch Node sẽ lưu giá trị lớn nhất của leaf node tương ứng. Ví dụ trong Leaf Node đầu tiên, giá trị lớn nhất là 46, nên Branch Node đầu tiên lưu giá trị là 46, Leaf Node tiếp theo giá trị lớn nhất là 53, Branch Node lại lưu giá trị 53, cứ tiếp tục như vậy Branch Node có giá trị là 46,53,57,83. Tiếp tục tới các Node cha đều như vậy, cho đến khi tất cả các Key đều vừa vặn trong một Node, node đó gọi là root node. Cấu trúc này gọi là balanced search tree bởi vì khoảng cách từ root node tới leaf node luôn luôn bằng nhau với tất cả các node.
Sau khi index được tạo, mỗi khi insert, delete, update dữ liệu database đều cập nhật lại index vài giữ cho cây luôn cân bằng, điều này gây ra vấn đề hiệu năng, sẽ được trình bày ở phần sau. ( Khi nào trình bày mình sẽ nói tới) hoặc tham khảo tại đây
Vậy cái tree này tìm kiếm nhanh như thế nào? Mình sẽ mô tả cách duyệt tree như hình dưới.
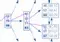
Giả sử mình cần tìm bản ghi có giá trị 57, cây bắt đầu duyệt từ root node, cây sẽ duyệt theo thứ tự tăng dần, cho tới khi tìm thấy bản ghi giá trị lớn hơn hoặc bằng giá trị cần tìm (>= 57). Trên hình là 83, sau đó cây sẽ tìm tới Branch node chứa số 83 (trên hình là branch chứa các số 46,53,57,83) rồi cứ tiếp tục như vậy cho tới leaf node và tìm được bản ghi cần tìm. Việc duyệt cây này rất nhanh dù với dữ liệu siêu to khổng lồ đi nữa. Nó cho phép tìm tới bất cứ một node lá nào với số bước như nhau, và độ sâu của cây tăng theo mức logarit với dữ liệu, nghĩa là số liệu tăng rất nhanh thì độ sâu của cây chỉ tăng lên một chút. Các index trong thực tế với hàng triệu bản ghi thường chỉ có độ sâu là 4 hoặc 5, cây với độ sâu là 6 rất hiếm gặp.
Tại sao lại như vậy, mình sẽ giải thích chút về logarit, chắc mọi người đều học từ cấp 3 rồi nên mình sẽ giải thích trong ví dụ. Trong hình đầu tiên, độ sâu của cây là 3, mỗi một node lại chứa 4 cục, vì vậy tổng có thể chứa được 64 cục ( ), nếu tăng độ sâu lên 1 cây có thể chứa được () =256 cục, cứ mỗi một level tăng lên thì số lượng cục index chứa được lại tăng gấp 4. Logarit là ngược lại hàm mũ, nên hiểu là nếu số lượng bản ghi tăng gấp 4 lần thì độ sâu của cây chỉ tăng 1 lần. Độ sâu của cây là (số lượng cục index). Các bạn có thể xem bảng dưới
| Độ sâu của cây | Số lượng bản ghi |
|---|---|
| 3 | 64 |
| 4 | 256 |
| 5 | 1,024 |
| 6 | 4,096 |
| 7 | 16,384 |
| 8 | 65,536 |
| 9 | 262,144 |
| 10 | 1,048,576 |
Trên bảng trên bạn thấy có thể tìm kiểm hàng triệu bản ghi chỉ với 10 tree level, trong thực tế nó còn ngon hơn nhiều yếu tố chính ảnh hưởng tới độ sâu là số cục trên một node, số cục càng lớn, cây càng nông hơn, duyệt càng nhanh hơn. Database cố gắng nhét càng nhiều cục càng tốt vào một node, tới hàng trăm vì vậy với dữ liệu lớn gấp hàng trăm lần thì số level mới tăng lên 1. Vì vậy nhiều khi bạn sẽ choáng váng khi tìm kiếm một trường trước khi đánh và sau khi đánh index, và sẽ thấy dữ liệu tăng gấp vài lần mà tốc độ vẫn không hề thay đổi.
PS: các bạn có thể tham khảo mô phỏng B-Tree tại đây nhé!