I. Bài toán Tìm kiếm nhị phân tổng quát

Ở bài viết trước, mình đã giới thiệu tới các bạn những khái niệm cơ bản nhất về bài toán tìm kiếm trong Tin học, cũng như giới thiệu về hai giải thuật Tìm kiếm tuần tự và Tìm kiếm nhị phân. Trong bài viết này, mình sẽ tập trung nói về giải thuật Tìm kiếm nhị phân, nhưng sẽ là áp dụng trong một lớp bài toán tổng quát hơn rất nhiều.

Ứng dụng trong việc tìm kiếm một khóa trên tập cho trước chỉ là một ứng dụng cơ bản của giải thuật Tìm kiếm nhị phân. Trên thực tế, Tìm kiếm nhị phân có thể được mở rộng để áp dụng cho một lớp bài toán tổng quát hơn nhiều, cụ thể là tìm kiếm kết quả trên một hàm số đơn điệu nhận tham số đầu vào là một số nguyên. Hàm số đơn điệu hiểu đơn giản là một hàm tăng hoặc hàm giảm, ví dụ như dãy số đã sắp xếp tăng dần trong bài toán cơ bản có thể coi là một hàm tăng.

Về bản chất, giải thuật Tìm kiếm nhị phân là một giải thuật phát triển từ thiết kế giải thuật Giảm để trị (Decrease and Conquer), nghĩa là tìm cách thu hẹp khoảng cách tìm kiếm lại ở mỗi bước, cho tới khi hai đầu mút của khoảng tìm kiếm chạm vào nhau, thì điểm chạm đó chính là kết quả bài toán. Còn nếu hai đầu mút không thể chạm vào nhau, nghĩa là kết quả bài toán không tồn tại.

Mặt khác, trong bài toán tìm kiếm nhị phân, kết quả bài toán đó thường phải thỏa mãn một tập điều kiện $C$ . Điều này dẫn đến việc cần phải xây dựng một hàm kiểm tra $P:S \rightarrow \text{true},$ với $S$ là không gian tìm kiếm chứa các ứng cử viên cho kết quả bài toán, còn hàm $P$ sẽ nhận vào một ứng cử viên $x \in S$ và trả về giá trị $\text{true, false}$ cho biết ứng cử viên đó có đáp ứng tập điều kiện $C$ hay không? Chẳng hạn, trong bài toán tìm kiếm nhị phân cơ bản (xem lại bài viết trước), thì đề bài có thể được viết lại thành: "Tìm chỉ số nhỏ nhất sao cho phần tử ở chỉ số đó có khóa lớn hơn hoặc bằng $k?$ ". Khi đó, không gian tìm kiếm $S$ ban đầu sẽ bao gồm các giá trị $[1, 2,..., n]$ (mọi chỉ số của mảng), và hàm $P(x) = \text{(boolean)}(a_x.key \ge k)$ trả về $\text{true}$ nếu $a_x.key \ge k$ và trả về $\text{false}$ nếu $a_x.key < k$ .

II. Điều kiện áp dụng giải thuật Tìm kiếm nhị phân

1. Định lý chính (Main Theorem) của Tìm kiếm nhị phân

Khi các bạn bắt đầu giải một bài toán và dự đoán rằng nó có thể giải quyết bằng Tìm kiếm nhị phân, thì việc chứng minh tính đúng đắn của dự đoán đó là rất cần thiết. Rất may mắn, chúng ta có một định lý cho biết khi nào một bài toán có thể áp dụng Tìm kiếm nhị phân, đó là Định lý chính (Main Theorem).

Định lý chính cho biết rằng: Một bài toán với không gian chứa các ứng cử viên là $S$ chỉ có thể áp dụng Tìm kiếm nhị phân nếu và chỉ nếu hàm kiểm tra $P$ của bài toán thỏa mãn:

$\{\forall x, y \in S \ | \ y > x \ \wedge \ P(x) = \text{true}\} \Rightarrow P(y) = \text{true} \ (1)$

Điều này cũng tương đương với tính chất:

$\{\forall x, y \in S \ | \ y < x \ \wedge \ P(x) = \text{false}\} \Rightarrow P(y) = \text{false} \ (2)$

Dễ thấy, nếu ta xây dựng hàm $P(x)$ cho mọi phần tử $x \in S,$ thì ta sẽ thu được một dãy liên tiếp các giá trị $\text{false}$ liền kề với một dãy liên tiếp các giá trị $\text{false}$ . Ngoài ra, chỉ cần điều chỉnh hàm $P$ theo hướng ngược lại, các bạn cũng sẽ xây dựng được định lý chính tạo ra hàm $P(x)$ là một dãy gồm toàn giá trị $\text{true}$ ở phía trước, theo sau là một dãy gồm toàn giá trị $\text{false}$ . Tuy nhiên ở đây mình chỉ viết một trường hợp để tránh dài dòng.

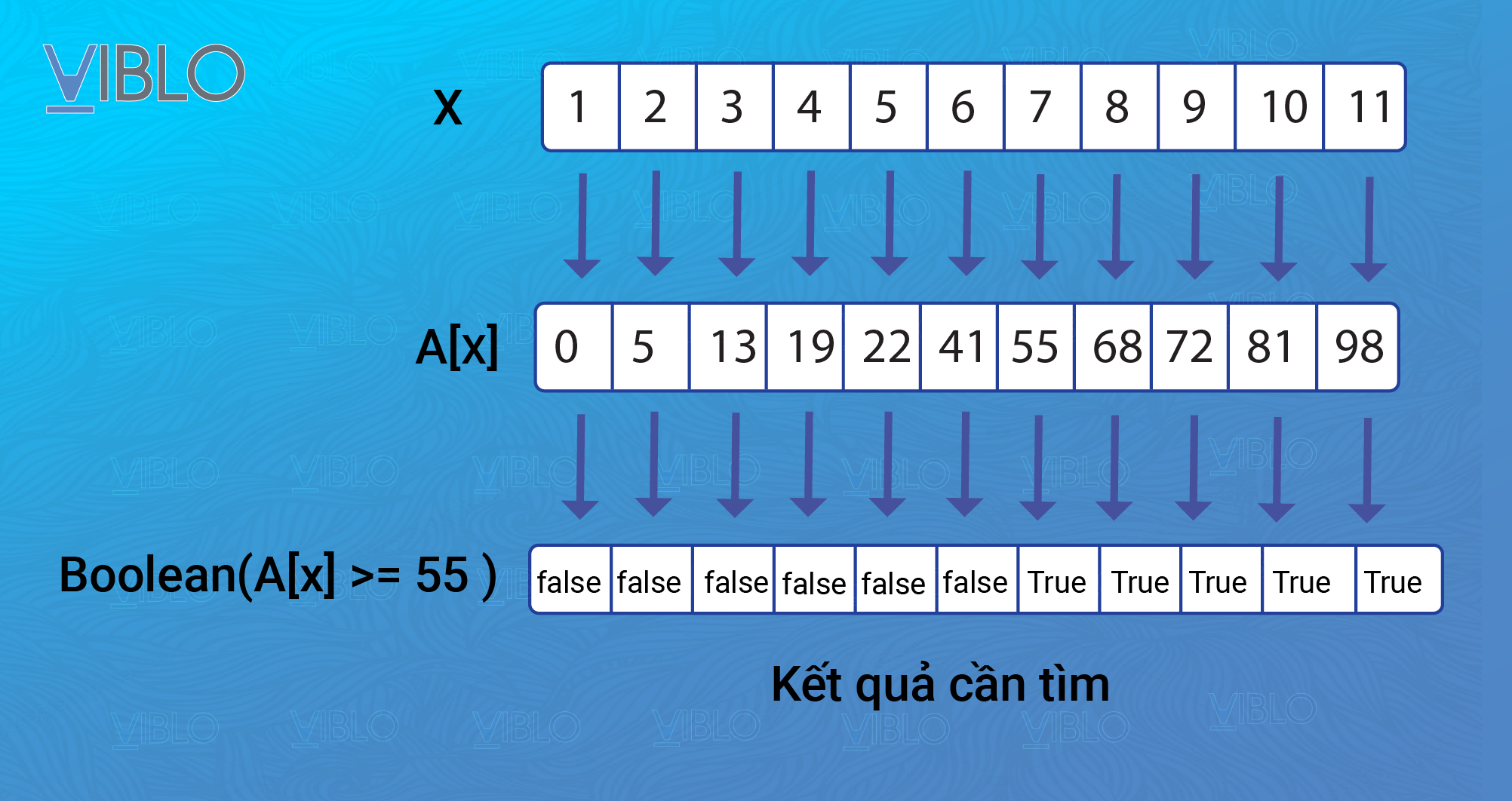
Minh họa việc xây dựng hàm $P(x)$ cho bài toán xác định vị trí của phần tử $k = 55$ trong mảng bằng tìm kiếm nhị phân

Từ những điều trên, các bạn sẽ xây dựng được một thông tin rất quan trọng, đó là điều kiện cần và đủ để một bài toán có thể giải được bằng tìm kiếm nhị phân. Cùng phân tính hai tính chất của định lý chính để làm rõ điều này:

Tính chất $(1)$ cho biết: Nếu $x$ hợp lệ thì mọi phần tử $y > x$ đều hợp lệ. Tính chất này giúp chúng ta loại đi nửa sau của không gian tìm kiếm do đã biết chắc $x$ là phần tử nhỏ nhất trong nửa sau hợp lệ, ta ghi nhận $x$ là kết quả tạm thời và tiếp tục tìm xem có phần tử nào ở nửa đầu (nhỏ hơn $x$ ) hợp lệ hay không.
Tính chất $(2)$ cho biết: Nếu $x$ không hợp lệ thì mọi phần tử $y < x$ đều không hợp lệ. Tính chất này giúp chúng ta loại đi nửa trước của không gian tìm kiếm do đã biết chắc chúng không hợp lệ, ta chỉ quan tâm những phần tử ở nửa sau (lớn hơn $x$ ) mà ta chưa biết thông tin chúng có hợp lệ hay không.

Vì dãy kiểm tra $P(S)$ đã là một tập gồm hai đoạn $\text{true - false}$ liên tiếp nhau, nên áp dụng tìm kiếm nhị phân, các bạn hoàn toàn có thể tìm ra giá trị $x$ nhỏ nhất thỏa mãn $P(x) = \text{true},$ hoặc giá trị $x$ lớn nhất thỏa mãn $P(x) = \text{false}$ . Điều mấu chốt ở đây chỉ còn lại là làm sao xây dựng được một hàm $P$ hợp lý với điều kiện trong định lý chính.

Như vậy, mình có thể tổng kết dấu hiệu nhận biết các bài toán tìm kiếm nhị phân dạng tổng quát như sau:

Đề bài yêu cầu tìm kết quả lớn nhất hoặc nhỏ nhất (còn gọi là bài toán tối ưu).
Giả sử đề bài yêu cầu tìm kết quả lớn nhất thỏa mãn tập điều kiện $C$ . Nếu như có thể nhận xét được rằng: Chỉ cần tồn tại một kết quả $X$ thỏa mãn tập điều kiện $C$ thì mọi kết quả nhỏ hơn $X$ đều thỏa mãn tập điều kiên $C,$ thì kết quả lớn nhất có thể tìm được bằng tìm kiếm nhị phân (áp dụng định lý chính).
Trong trường hợp đề bài yêu cầu tìm kết quả nhỏ nhất, thì ta xây dựng định lý chính ngược lại.

2. Cài đặt tổng quát

Trước khi cài đặt giải thuật Tìm kiếm nhị phân, các bạn cần phải trả lời những câu hỏi sau:

Các giá trị $P(x)$ của hàm kiểm tra $P$ đã có dạng $\text{false - true}$ ( $\text{false}$ liên tiếp rồi tới $\text{true}$ ) hoặc ngược lại hay chưa? Cài đặt tổng quát phía dưới sẽ mặc định dãy $P(x)$ có dạng $\text{false - true},$ nếu các bạn muốn làm ngược lại thì chỉ cần đảo hàm $P$ là xong.
Mục tiêu của các bạn là tìm phần tử $x$ nhỏ nhất thỏa mãn $P(x) = \text{true}$ hay tìm phần tử $x$ lớn nhất thỏa mãn $P(x) = \text{false}?$ Mình sẽ trình bày cả hai cách bên dưới.
Phạm vi tìm kiếm đã đủ rộng hay chưa? Nhiều trường hợp các bạn có thể chọn một phạm vi tìm kiếm thật lớn mà không sợ bị quá thời gian, vì thời gian thực thi của giải thuật chỉ là $O\big(\log(n)\big),$ miễn là khoảng tìm kiếm đó chắc chắn chứa nghiệm của bài toán.
Nếu bài toán có nghiệm, hãy đảm bảo rằng khoảng tìm kiếm $[l, r]$ phải là một khoảng đóng luôn luôn chứa nghiệm của bài toán (tức là phải tồn tại $x$ nhỏ nhất thỏa mãn $P(x) = \text{true}$ trong khoảng này).
Không gian tìm kiếm có chứa số âm hay không? Nếu không gian tìm kiếm có chứa số âm thì việc chọn $\text{mid} = \left \lfloor{\frac{(l + r)}{2}} \right \rfloor$ sẽ gây ra lỗi, mình sẽ giải thích cụ thể bên dưới. Mặc định các cài đặt dưới đây sẽ coi khoảng tìm kiếm ở dạng tổng quát gồm cả các số âm.

Cài đặt 1: Tìm $x$ nhỏ nhất mà $P(x) = \text{true}$ :

bool P(int x)
{ // Logic của hàm kiểm tra. return true; // Thay bằng logic phù hợp với bài toán.
} int binary_searching(int l, int r)
{ // Biến res dùng để lưu nghiệm tối ưu, ban đầu gán nó bằng l - 1,  // coi như chưa có nghiệm. int res = l - 1; while (l <= r) { int mid = l + (r - l) / 2; if (P(mid) == true) { res = mid; r = mid - 1; } else l = mid + 1; } // Nếu res = l - 1 giống như ban đầu thì bài toán vô nghiệm. if (res == l - 1) return -1; return res;
}

Cài đặt 2: Tìm $x$ lớn nhất mà $P(x) = \text{false}$ :

bool P(int x)
{ // Logic của hàm kiểm tra. return true; // Thay bằng logic phù hợp với bài toán.
} int binary_searching(int l, int r)
{ // Biến res dùng để lưu nghiệm tối ưu, ban đầu gán nó bằng l - 1,  // coi như chưa có nghiệm. int res = l - 1; while (l <= r) { int mid = l + (r - l) / 2; if (P(mid) == false) { res = mid; l = mid + 1; } else r = mid - 1; } // Nếu res = l - 1 giống như ban đầu thì bài toán vô nghiệm. if (res == l - 1) return -1; return res;
}

Bạn đọc có thể sẽ thắc mắc rằng tại sao không đặt $\text{mid} = \left \lfloor{\frac{(l + r)}{2}} \right \rfloor$ như ở giải thuật cơ bản, mà lại đặt $\text{mid} = l + \left \lfloor{\frac{(r - l)}{2}} \right \rfloor$ . Lí do là vì, ta luôn muốn kết quả phép chia được làm tròn xuống về gần với cận dưới (chẳng hạn như phần tử ở giữa của đoạn $[5, 10]$ sẽ là $7$ chứ không phải $8$ ). Nếu như trong khoảng tìm kiếm có số âm, thì khi $(l + r) < 0$ sẽ dẫn đến kết quả phép chia cho $2$ bị làm tròn lên. Tuy nhiên, trong phần lớn trường hợp, việc tìm kiếm chỉ diễn ra trên tập số nguyên không âm nên vấn đề nói trên sẽ không xảy ra.

III. Tìm kiếm nhị phân trên tập số thực

Tìm kiếm nhị phân cũng có thể được áp dụng khi không gian tìm kiếm là một đoạn số thực. Thường thì việc xử lý sẽ đơn giản hơn với số nguyên do ta không phải bận tâm về việc dịch chuyển cận, chỉ cần gán trực tiếp $l = mid$ hoặc $r = mid,$ do đối với số thực thì hai cận không bao giờ chạm hẳn vào nhau được.

Đối với số thực, ta sẽ không thể tìm được một kết quả chính xác, mà chỉ thu được kết quả xấp xỉ. Giải pháp ở đây là sử dụng độ chính xác epsilon: Dừng thuật toán khi $r - l \le eps$ (thường $eps$ rất nhỏ, rơi vào khoảng $10^{-8}$ là an toàn). Phương pháp này thường được sử dụng chủ yếu, đặc biệt trong các bài toán có thời gian ràng buộc chặt.

Cài đặt: Dưới đây là cài đặt tìm $x$ nhỏ nhất thỏa mãn $P(x) = \text{true}$ :

bool P(double x)
{ // Logic của hàm kiểm tra. return true; // Thay bằng logic phù hợp với bài toán.
} double binary_searching(double l, double r)
{ double eps = 1e-8; while (r - l > eps) { double mid = l + (r - l) / 2; if (P(mid) == false) r = mid; else l = mid; } // trung bình cộng lo và hi xấp xỉ ranh giới giữa false và true. return l + (r - l) / 2;
}

IV. Bài toán ví dụ

Nếu như các bạn vẫn còn cảm thấy khó hiểu sau khi đọc xong những lý thuyết dài dòng bên trên, thì hãy cùng nhau đi vào một số bài toán ví dụ để hiểu thêm về cách áp dụng tìm kiếm nhị phân trong bài toán tối ưu nha!

Bài toán 1

Một xưởng gói quà công nghiệp có $n \ (1 \le n \le 10^5)$ món quà khác nhau cần gói. Để giảm thiểu thời gian gói quà, công ty này sử dụng một dây chuyền gồm $m \ (1 \le m \le 10^5)$ máy gói quà tự động, máy thứ $i$ có thời gian gói là $t_i \ (t_i \le 10^9, 1≤i≤m)$ . Do thời gian gấp rút, công ty muốn tính toán xem cần tối thiểu bao lâu để $n$ món quà được gói xong.

Yêu cầu: Hãy tính thời gian tối thiểu để $n$ món quà được gói xong? Coi rằng mỗi máy gói quà đều có thể gói liên tục, bỏ qua thời gian vận chuyển các món quà.

Ý tưởng:

Cách làm đơn giản nhất là duyệt qua tất cả các thời gian $t \le \text{max}(t_i),$ kiểm tra xem với thời gian đó thì tổng số món quà gói được bằng bao nhiêu? Nếu tổng số đó lớn hơn hoặc bằng $n$ thì đáp án chính là $t$ . Dễ thấy cách làm này có độ phức tạp $O(\text{max}(a_i) \times n),$ không thể vượt qua ràng buộc về thời gian.
Có thể cải tiến dựa trên nhận xét sau: Nếu như trong thời gian $T$ mà có thể gói được hết $n$ món quà, thì trong các thời gian lớn hơn $T$ tất nhiên cũng có thể gói được hết $n$ món quà (chính là tính chất $(1)$ của định lý chính). Vì thế, chỉ cần quy về tìm kiếm các thời gian trên đoạn $[1, T - 1]$ . Ngược lại, nếu trong thời gian $T$ không thể gói hết $n$ món quà, thì cần tìm kiếm kết quả trên đoạn $[T + 1, \text{max}(t_i)]$ . Liên tục lặp lại quá trình chia đôi đoạn tìm kiếm tới khi hai đầu mút chạm vào nhau, ta thu được kết quả tối ưu.

Cài đặt:

#include <bits/stdc++.h>
#define int long long
#define task "Mintime." using namespace std;
const int maxn = 1e6 + 10;
int n, m, t[maxn]; void enter()
{ cin >> n >> m; for (int i = 1; i <= m; ++i) cin >> t[i];
} // Kiểm tra xem có thể gói được n món quà trong thời gian time_val không.
bool check_valid(int time_val)
{ int presents = 0; for (int i = 1; i <= m; ++i) presents += (time_val / t[i]); return presents >= n;
} void solution()
{ // Tìm kiếm nhị phân thời gian tối ưu. int best_time = 0, l = 1, r = 1e9 + 10; while (l <= r) { int mid = (l + r) >> 1; if (check_valid(mid)) { best_time = mid; r = mid - 1; } else l = mid + 1; } cout << best_time;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); enter(); solution(); return 0;
}

Bài toán 2

Với một xâu kí tự $S,$ ta định nghĩa $|S|$ là độ dài của xâu đó. Các kí tự trong xâu $S$ được đánh số thứ tự từ $1$ theo chiều từ trái qua phải. Xâu tiền tố độ dài $k$ của $S,$ viết tắt là $C(S, k)$ được định nghĩa như sau:

$C(S, k) = \begin{cases}S_1S_2...S_k; \text{với } k \le |S|.\\ S; \text{với } k > |S|. \end{cases}$

Cho trước $n \ (1 \le n \le 10^5)$ xâu kí tự $S_1, S_2,..., S_n$ có tổng độ dài không vượt quá $10^6$ . Với một giá trị $k$ bất kỳ, ta xây dựng tập các xâu $T_1, T_2,..., T_n;$ với $T_i = C(S_i, k) \ (1 \le i \le n)$ .

Yêu cầu: Tìm giá trị $k$ nhỏ nhất để tập các phần tử $T_1, T_2,..., T_n$ là đôi một phân biệt?

Ý tưởng: Bài toán này có thể làm bằng quy hoạch động, tuy nhiên ở đây mình vẫn giới thiệu phương pháp tìm kiếm nhị phân để các bạn hiểu rõ hơn cách áp dụng thuật toán. Nhận xét thấy, nếu như với giá trị $k$ mà các xâu con độ dài $k$ đều phân biệt, thì các xâu con độ dài lớn hơn $k$ cũng sẽ phân biệt (tính chất $(1)$ của định lý chính). Vì vậy, đây là một bài toán thỏa mãn tính chất tìm kiếm nhị phân.

Từ đây, ta tìm kiếm nhị phân giá trị $k$ nhỏ nhất, ứng với mỗi giá trị $k,$ duyệt qua $n$ xâu để tìm ra xâu con độ dài $k$ của từng xâu và sử dụng map để kiểm tra xem xâu con đó đã xuất hiện hay chưa. Nếu cả $n$ xâu con đều phân biệt thì có thể giảm $k$ xuống, ngược lại tăng $k$ lên.

Cài đặt:

#include <bits/stdc++.h> using namespace std; const int maxn = 1e5 + 10;
string s[maxn];
int n, maxl; void enter()
{ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin >> n; for (int i = 1; i = n; ++i) { cin >> s[i]; s[i] = ' ' + s[i]; maxl = max(maxl, (int)s[i].size() - 1); }
} // Kiểm tra xem với độ dài k thì đã thu được n xâu con phân biệt hay chưa.
bool check(int k)
{ map < string, bool > mark; for (int i = 1; i <= n; ++i) { string st = (mid <= (int)s[i].size() - 1) ? s[i].substr(1, mid) : s[i]; if (mark[st]) return false; mark[st] = true; } return true;
} void solve()
{ // Tìm kiếm nhị phân giá trị k tốt nhất. int l = 1, r = maxl + 1, res = 0; while (l <= r) { int mid = (l + r) >> 1; if (!check(mid)) l = mid + 1; else { res = mid; r = mid - 1; } } cout << res;
} int main()
{ enter(); solve(); return 0;
}

Tìm kiếm 5.2: Giải thuật Tìm kiếm nhị phân nâng cao

I. Bài toán Tìm kiếm nhị phân tổng quát

II. Điều kiện áp dụng giải thuật Tìm kiếm nhị phân

1. Định lý chính (Main Theorem) của Tìm kiếm nhị phân

2. Cài đặt tổng quát

III. Tìm kiếm nhị phân trên tập số thực

IV. Bài toán ví dụ

Bài toán 1

Bài toán 2

V. Tài liệu tham khảo

Bình luận

Bài viết tương tự

Thuật toán quay lui (Backtracking)

Các thuật toán cơ bản trong AI - Phân biệt Best First Search và Uniform Cost Search (UCS)

Sử dụng vector trong lập trình C++ - giải bài toán lập trình muôn thủa

MÔ PHỎNG THUẬT TOÁN VƯƠNG HẠO TRONG PROLOG

A* Search Algorithm

Python: Jump Search