I. Xác định chu trình trên đồ thị

Từ những bài viết đầu tiên về chuyên đề Lý thuyết đồ thị, tôi đã giới thiệu tới các bạn khái niệm về Chu trình trên đồ thị. Một đường đi $\{v_0, v_1, v_2, \dots, v_k\}$ trên đồ thị được gọi là một chu trình nếu như $v_0 = v_k,$ và nếu như các cạnh trên đường đi đó đều phân biệt. Ngoài ra, trên đồ thị còn có thể tồn tại hai dạng chu trình đặc biệt là Chu trình Euler và Chu trình Hamilton, sẽ được đề cập tới ở những bài viết tiếp theo.

Trong bài viết này, chúng ta sẽ cùng nhau đi sâu hơn vào cách xác định chu trình trên đồ thị và những bài toán ứng dụng của nó.

Giải thuật $\text{DFS}$ là một công cụ rất hữu hiệu để xác định chu trình trên đồ thị. Sau đây, chúng ta sẽ cùng tìm hiểu về ý tưởng của giải thuật.

1. Phát biểu bài toán

Cho một đơn đồ thị vô hướng $G$ gồm $n$ đỉnh và $m$ cung (có thể có "khuyên" - cạnh tự nối một đỉnh với chính nó). Các đỉnh của đồ thị được đánh số từ $1$ tới $n$ .

Một chu trình trên đồ thị là một đường đi $(x_1, x_2, \dots, x_k, x_1)$ với hai đỉnh đầu và cuối của đường đi giống nhau.

Hãy xác định đồ thị trên có chứa chu trình nào hay không?

Input:

Dòng đầu tiên chứa hai số nguyên $n$ và $m$ - số đỉnh và số cạnh của đồ thị $(1 \le n, m \le 10^5)$ .
$m$ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương $u, v$ - thể hiện một cạnh của đồ thị nối hai đỉnh $u$ và $v$ .

Output:

In ra YES nếu đồ thị có chứa chu trình, ngược lại in ra NO.

Sample Input 1:

Sample Output 1:

YES

Sample Input 2:

Sample Output 2:

NO

2. Ý tưởng

Phân loại các cung trên cây DFS

Trong quá trình duyệt $\text{DFS}$ trên đồ thị, nếu như ta chỉ giữ lại các cạnh $(u, v)$ với $u$ là cha của $v,$ rồi định hướng cạnh đó theo chiều $(u \rightarrow v),$ thì ta sẽ thu được một đồ thị mới dạng cây, gọi là cây $\text{DFS}$ . Các cạnh được giữ lại sẽ gọi là cạnh thuộc cây $\text{DFS},$ còn các cạnh không được giữ lại gọi là cạnh không thuộc cây $\text{DFS}$ .

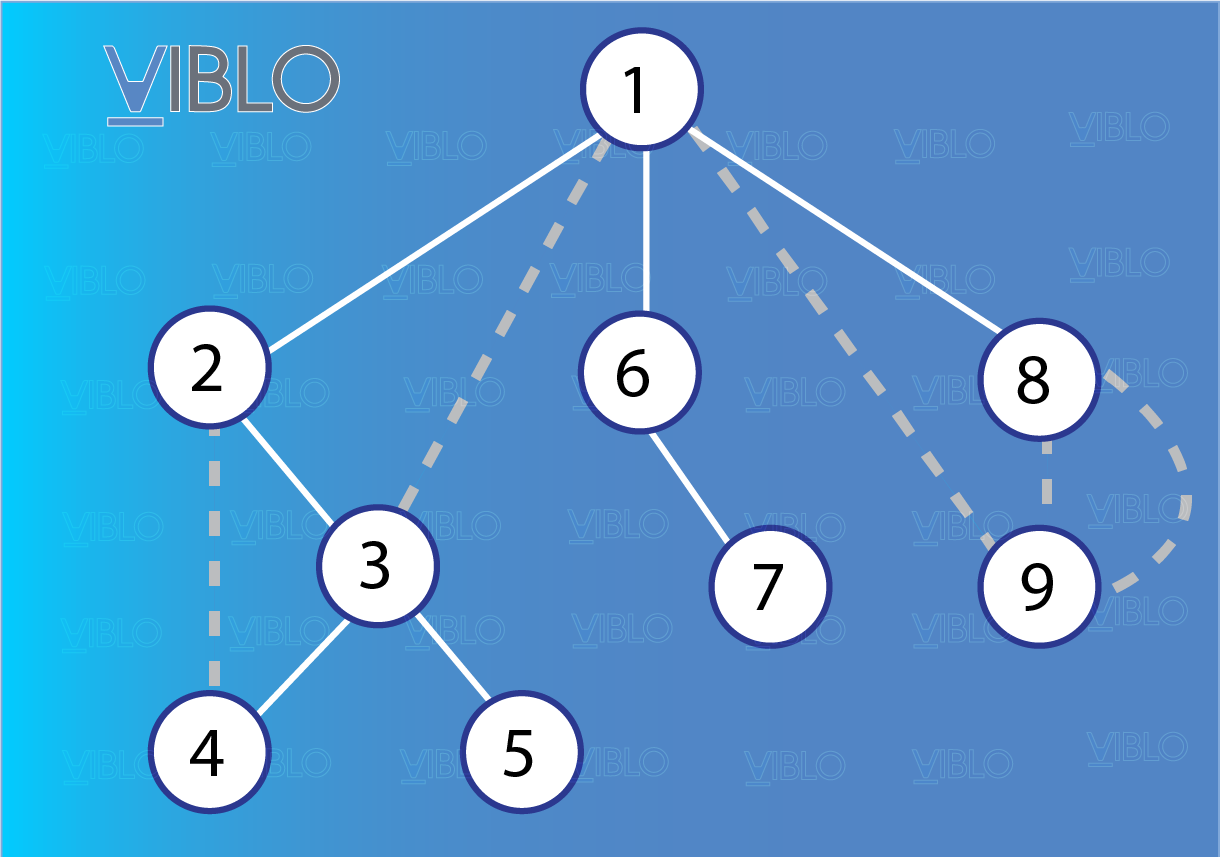
Cây DFS của một đồ thị gồm 9 đỉnh, các cạnh màu trắng là cạnh được giữ lại

Giả sử đồ thị đang xét là đồ thị có hướng, xét mọi cung được thăm và không được thăm trong quá trình $\text{DFS},$ ta có các loại cung sau:

Cung của cây DFS (Tree Edges): Các cung được thăm trong quá trình $\text{DFS}$ (cung màu trắng nét liền).
Cung xuôi (Forward edges): Cung không thuộc cây $\text{DFS}$ có dạng $(u \rightarrow v)$ ; trong đó $u$ là cha của $v$ trong quá trình $\text{DFS}$ (cạnh xanh lá).
Cung ngược (Back edges): Cung không thuộc cây $\text{DFS}$ và có dạng $(v \rightarrow u)$ ; trong đó $u$ là cha của $v$ (cạnh đỏ) nhưng $v$ đã được thăm trước đó do một dây chuyền $\text{DFS}$ khác.
Cung chéo (Cross edges): Cung không thuộc cây $\text{DFS}$ , trong đó $u$ và $v$ thuộc hai nhánh khác nhau của cùng một cây $\text{DFS}$ (cạnh tím).

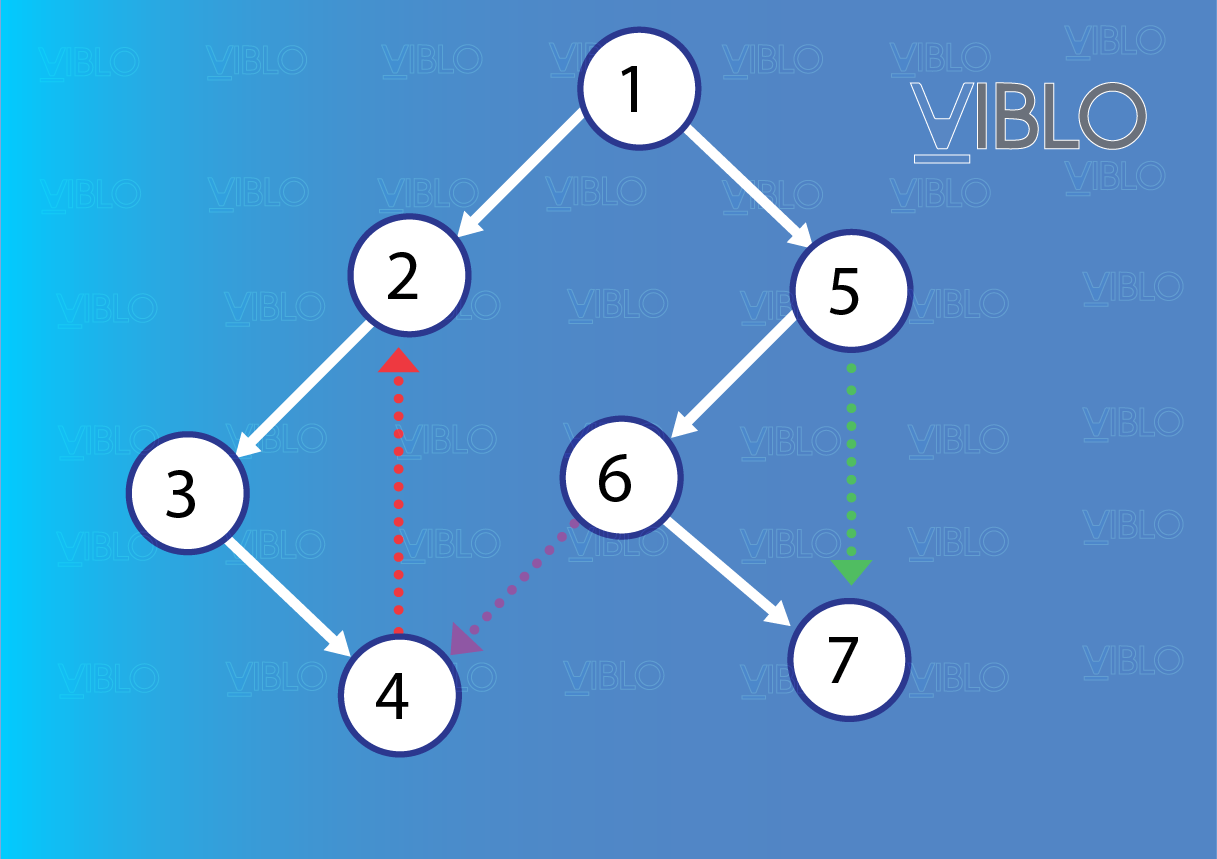
Còn nếu như xét trên đồ thị vô hướng, thì chỉ tồn tại duy nhất hai loại cung là cung thuộc cây DFS và cung ngược (không thuộc cây DFS).

Phân tích giải thuật

Từ định nghĩa về cây $\text{DFS}$ ở trên, ta nhận thấy rằng:

Một cây $\text{DFS}$ của đồ thị sẽ chứa toàn bộ các đỉnh thuộc cùng một thành phần liên thông của đồ thị, nhưng không phải tất cả các cạnh.
Cây $\text{DFS}$ của đồ thị là một đồ thị không có chu trình.
Nếu như trong quá trình duyệt $\text{DFS},$ xuất hiện một cung ngược, thì chắc chắn thành phần liên thông hiện tại có chứa chu trình (bời vì sẽ có một đường đi quay lại được đỉnh đã thăm ở phía trên).

Nhận xét trên cho ta ý tưởng về cách xác định một đồ thị có chu trình hay không vô cùng đơn giản như sau:

Sử dụng DFS, duyệt từng thành phần liên thông của đồ thị. Nếu trong quá trình duyệt phát hiện một cung ngược, thì chắc chắn đồ thị có chứa chu trình.

Việc xác định một cung có phải cung ngược hay không rất dễ, bằng cách sử dụng một mảng $\text{visited}[u]$ để đánh dấu lại đỉnh $u$ đã duyệt qua hay chưa. Sau đó, nếu như trong quá trình duyệt nhánh $text{DFS}$ gốc $u$ mà có một cạnh $(u, v)$ mà $v$ đã thăm rồi, thì cung $(u \rightarrow v)$ sẽ là cung ngược.

Giải thuật có thể thực hiện tương tự nhau ở cả đồ thị vô hướng lẫn có hướng.

3. Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define int long long
#define task "detect_cycle." using namespace std; const int maxn = 1e5 + 10;
typedef int arr[maxn];
vector < int > adj[maxn]; // Nhập dữ liệu đồ thị.
void enter(int &n, int &m, vector < int > adj[])
{ cin >> n >> m; for (int u = 1; u <= n; ++u) adj[u].clear(); for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); adj[v].push_back(u); }
} // DFS để tìm chu trình từ một cây DFS gốc u.
bool dfs_find_cycle(int u, int par, vector < int > adj[], arr visited)
{ visited[u] = true; for (int v: adj[u]) { // Nếu đỉnh v chưa thăm thì đi thăm v và xem nhánh DFS từ v // có tạo ra chu trình hay không. if (!visited[v]) { if (dfs_find_cycle(v, u, adj, visited)) return true; } // Nếu v đã thăm và v không phải đỉnh vừa gọi đệ quy ở bước // trước, thì cung (u, v) là một cung ngược -> có chu trình. else if (v != par) return true; } return false;
} // Xác định có tồn tại chu trình trên đồ thị hay không.
void solution(int n, vector < int > adj[], arr visited)
{ fill(visited + 1, visited + n + 1, 0); // Thử DFS từ các đỉnh và dựng cây DFS. for (int u = 1; u <= n; ++u) if (!visited[u]) { if (dfs_find_cycle(u, -1, adj, visited)) { cout << "YES" << endl; return; } } cout << "NO" << endl;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(nullptr); int n, m; arr visited; enter(n, m, adj); solution(n, adj, visited); return 0;
}

II. Ví dụ minh họa

1. Bài toán 1

Đề bài

Cho một dãy số $A$ gồm $n$ phần tử $a_0, a_1, \dots, a_{n - 1}$ . Xuất phát từ một phần tử ở vị trí $i$ bất kỳ, ta sẽ di chuyển trên mảng theo trình tự sau:

Nếu $a_i < 0,$ di chuyển tới phần tử $(i - a_i) \text{ mod } n$ .
Nếu $a_i > 0,$ di chuyển tới phần tử $(i + a_i) \text{ mod } n$ .

Nếu như giá trị $a_i \text{ mod } n = 0,$ thì sẽ không có sự di chuyển nào diễn ra cả.

Hãy xác định xem quá trình di chuyển trên có thể tạo thành một chu trình di chuyển trên dãy số hay không? Lưu ý rằng, nếu như bước di chuyển tự đi tới chính nó thì không tính là một chu trình.

Input:

Dòng đầu tiên chứa số nguyên dương $n \ (1 \le n \le 10^5)$ .
Dòng thứ hai chứa $n$ số nguyên $a_0, a_1, \dots, a_{n - 1}$ phân tách nhau bởi dấu cách $\big(|a_i| \le 10^6; a_i \ne 0, \forall i: 0 \le i < n\big)$ .

Output:

In ra YES nếu như có thể tạo ra một chu trình di chuyển trên dãy số, ngược lại in ra NO.

Sample Input 1:

5
2 -1 1 2 2

Sample Output 1:

YES

Sample Input 2:

2
1 2

Sample Output 2:

NO

Ý tưởng

Nếu như ta đồ thị hóa bài toán, coi các vị trí $i$ trên dãy số là các đỉnh của một đồ thị, và giữa hai vị trí $i, j$ có cạnh nối nếu như từ vị trí $i$ có thể di chuyển được tới vị trí $j$ theo cách di chuyển trong đề bài, thì bài toán sẽ trở thành xác định xem trên đồ thị có tồn tại chu trình hay không.

Trước tiên sử dụng một mảng $\text{adj}[u]$ để lưu các vị trí mà từ vị trí $u$ có thể di chuyển tới được, coi như đây là một danh sách kề của đồ thị. Sau đó tiến hành $\text{DFS}$ tìm đường như giải thuật bên trên.

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define int long long
#define task "loop_in_seq."
#define inf 1e9 + 7
#define x first
#define y second using namespace std; const int maxn = 1e5 + 10;
typedef int arr[maxn];
vector < int > adj[maxn]; // Nhập dữ liệu dãy số.
void enter(int &n, arr a)
{ cin >> n; for (int i = 0; i < n; ++i) cin >> a[i];
} // Dựng đồ thị.
void create_graph(int n, arr a, vector < int > adj[])
{ for (int i = 0; i < n; ++i) if (i != (i + a[i] + n) % n) adj[i].push_back((i + a[i] + n) % n);
} // DFS để tìm chu trình từ một cây DFS gốc u.
bool dfs_find_cycle(int u, int par, vector < int > adj[], arr visited)
{ visited[u] = true; for (int v: adj[u]) { // Nếu đỉnh v chưa thăm thì đi thăm v và xem nhánh DFS từ v // có tạo ra chu trình hay không. if (!visited[v]) { if (dfs_find_cycle(v, u, adj, visited)) return true; } // Nếu v đã thăm và v không phải đỉnh vừa gọi đệ quy ở bước // trước, thì cung (u, v) là một cung ngược -> có chu trình. else if (v != par) return true; } return false;
} // Tìm chu trình trong dãy số.
void solution(int n, arr a, vector < int > adj[])
{ create_graph(n, a, adj); arr visited; fill(visited, visited + n, 0); for (int i = 0; i < n; ++i) if (!visited[i]) if (dfs_find_cycle(i, -1, adj, visited)) { cout << "YES"; return; } cout << "NO";
} main()
{ //freopen(task"inp", "r", stdin); //freopen(task"out", "w", stdout); ios_base::sync_with_stdio(false); cin.tie(nullptr); int n; arr a; enter(n, a); solution(n, a, adj); return 0;
}

Đánh giá độ phức tạp

Độ phức tạp chỉ là $O(n + m)$ cho quá trình $\text{DFS},$ với $m$ là số cạnh nối tạo ra trên đồ thị.

2. Bài toán 2

Đề bài

Cho một đơn đồ thị vô hướng liên thông gồm $n$ đỉnh, các đỉnh được đánh số từ $0$ và $m$ cạnh. Hãy đếm số lượng chu trình đơn có $k$ đỉnh và $k$ cạnh trong đồ thị đó?

Input:

Dòng đầu tiên chứa ba số nguyên dương $n, m$ và $k \ (2 \le n, m \le 100; 1 \le k \le m)$ .
$m$ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương $u, v$ - thể hiện đồ thị có một cạnh nối hai chiều giữa hai đỉnh $u$ và $v$ .

Output:

Số nguyên duy nhất là số lượng chu trình tìm được. Lưu ý, các chu trình có cùng các đỉnh và các cạnh nhưng khác thứ tự sẽ vẫn chỉ tính là $1$ chu trình.

Sample Input:

Sample Output:

Giải thích:

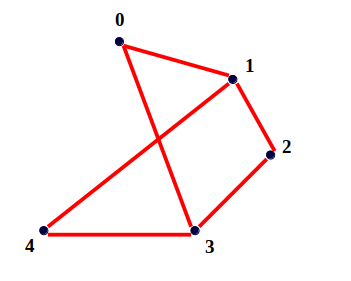
Các chu trình tìm được là: $(0, 1, 2, 3, 0); (0, 1, 4, 3, 0); (1, 2, 3, 4, 1)$ . Lưu ý rằng, hai chu trình $(0, 3, 2, 1, 0)$ và $(0, 1, 2, 3, 0)$ chỉ được tính $1$ lần, do đó đáp án chỉ là $3$ .

Ý tưởng

Thay vì tìm một chu trình có độ dài $n,$ ta có thể tìm ra các đường đi có độ dài $n - 1$ từ mọi đỉnh $u,$ sau đó kiểm tra xem đỉnh cuối cùng của đường đi tìm được có đến được đỉnh $u$ ban đầu hay không. Nếu có thì đó là một chu trình có độ dài $n$ .

Tuy nhiên, để giảm số lần phải duyệt chu trình, thì ta nhận xét rằng: Chỉ cần lựa chọn đỉnh xuất phát là một trong số $n - (k - 1)$ đỉnh đầu tiên. Lí do là bởi vì, nếu như thực sự tồn tại chu trình độ dài $k$ khi duyệt $\text{DFS}$ thì nhiệm vụ của chúng ta là phải tìm ra một đường đi độ dài $k - 1$ trong số $k - 1$ đỉnh còn lại. Việc chọn đỉnh xuất phát ngoài tập $n - (k - 1)$ đỉnh đầu tiên sẽ chỉ khiến cho số lượng chu trình trùng lặp bị tăng lên.

Một điều cần lưu ý là, mỗi khi chọn một đỉnh xuất phát để tìm chu trình từ nó, thì số lượng chu trình tìm được sẽ bị lặp lại $2$ lần (do chu trình có thể đi theo hai chiều xuôi chiều kim đồng hồ hoặc ngược chiều kim đồng hồ). Vì thế, kết quả cuối cùng cần chia cho $2$ .

Cài đặt

Ngôn ngữ C++:

#include <bits/stdc++.h>
#define task "count_cycle." using namespace std; const int maxn = 101;
typedef int arr[maxn];
vector < int > adj[maxn]; void enter(int &n, int &m, int &k, vector < int > adj[])
{ cin >> n >> m >> k; for (int i = 1; i <= m; ++i) { int u, v; cin >> u >> v; adj[u].push_back(v); adj[v].push_back(u); }
} void dfs(int start, int k, int u, vector < int > adj[], arr visited, int &total_cycle)
{ visited[u] = 1; // Đã tìm ra đường đi độ dài k - 1. if (k == 0) { // Loại bỏ đỉnh u khỏi chu trình để chọn đường đi khác. visited[u] = 0; // Kiểm tra xem đỉnh u có quay về được đỉnh xuất phát ban đầu không. // Nghĩa là đỉnh ban đầu nằm trong danh sách kề của đỉnh u. if (find(adj[u].begin(), adj[u].end(), start) != adj[u].end()) ++total_cycle; return; } // Tìm các đường đi có thể bằng DFS. Mục tiêu là tạo được đường đi // có độ dài bằng k - 1. for (int v: adj[u]) { if (visited[v]) continue; dfs(start, k - 1, v, adj, visited, total_cycle); } // Loại bỏ đỉnh u khỏi chu trình để chọn một đường đi khác. visited[u] = 0;
} void solution(int n, int k, vector < int > adj[])
{ arr visited; fill(visited, visited + n, 0); int total_cycle = 0; for (int u = 0; u < n - (k - 1); ++u) if (!visited[u]) { // Nếu u chưa thăm thì dựng tất cả các chu trình độ dài // n xuất phát từ u. dfs(u, k - 1, u, adj, visited, total_cycle); // Đánh dấu lại u đã sử dụng rồi, từ sau đây sẽ không tìm // thêm các chu trình chứa u nữa -> tránh lặp lại. visited[u] = 1; } // Chia 2 kết quả vì số chu trình đã đếm bị lặp lại hai lần. cout << total_cycle / 2;
} main()
{ ios_base::sync_with_stdio(false); cin.tie(nullptr); int n, m, k; enter(n, m, k, adj); solution(n, k, adj); return 0;
}

Đánh giá độ phức tạp

Ta thử chọn $n - (k - 1)$ đỉnh làm điểm bắt đầu của chu trình, và lại mất thêm $O(n + m)$ để thực hiện $\text{DFS}$ tìm chu trình, do đó độ phức tạp tổng quát sẽ là $O\big(n \times (n + m)\big)$ .

III. Tài liệu tham khảo

Vấn đề về Chu trình trên đồ thị

I. Xác định chu trình trên đồ thị

1. Phát biểu bài toán

2. Ý tưởng

Phân loại các cung trên cây DFS

Phân tích giải thuật

3. Cài đặt

II. Ví dụ minh họa

1. Bài toán 1

Đề bài

Ý tưởng

Cài đặt

Đánh giá độ phức tạp

2. Bài toán 2

Đề bài

Ý tưởng

Cài đặt

Đánh giá độ phức tạp

III. Tài liệu tham khảo

Bình luận

Bài viết tương tự

Thuật toán quay lui (Backtracking)

Các thuật toán cơ bản trong AI - Phân biệt Best First Search và Uniform Cost Search (UCS)

Sử dụng vector trong lập trình C++ - giải bài toán lập trình muôn thủa

MÔ PHỎNG THUẬT TOÁN VƯƠNG HẠO TRONG PROLOG

A* Search Algorithm

Python: Jump Search